ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 10271
Скачиваний: 94

101
Вариант 6
1. Решить задачу, используя диаграмму Эйлера-Венна.
Из 10 участников ансамбля шестеро умеют играть на гитаре, пятеро на
ударных инструментах, пятеро на духовых. Двумя инструментами владеют:
гитарой и ударными – трое, ударными и духовыми – двое, гитарой и духовыми
– четверо. Остальные участники ансамбля только поют. Сколько певцов в ан-
самбле?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
4
,
3
,
2
,
1
{
},
8
,
6
,
4
,
2
{
},
8
,
7
,
6
,
5
,
2
{
=
=
=
Z
Y
X
. Найти булеан множества
Y
и
какое-либо разбиение множества
Z
. Выполнить действия
)
(
\
Z
Y
X
∩
.
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
.
C
A
B
A
C
B
A
∩
∩
∩
∩
∩
∩
4. Пусть
}
5
,
4
,
3
,
2
,
1
{
=
X
. Бинарное отношение
X
X
R
×
⊆
задано ха-
рактеристическим свойством:
}
,
,
2
на
делится
)
,
{(
X
b
a
b
a
b
a
R
∈
+
=
.
Представить отношение
R
другими возможными способами. Какими
свойствами обладает это отношение? Является ли оно отношением эквива-
лентности?
5. Заданы отношения:
R: S:
A
1
A
2
B
1
B
2
B
3
s
t
s
u
t
u v u v t
x z z s x
Записать обозначения операций реляционной алгебры и выполнить их:
а) селекция отношения
S
по условию “
3
1
B
B
>
”;
б) соединение отношений
R
и
S
по условию “
2
1
B
A
=
”.
6. Даны множества
}
2
,
0
,
1
{
−
=
A
и
∈
−
=
n
n
B
1
3
{
N
}. Какова мощ-
ность множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. В библиотеку поступило девять новых различных книг. Сколькими
способами читатель может выбрать три из них?
8. В елочной гирлянде восемь лампочек: две желтых, три красных, три
синих. Сколькими способами их можно расположить в гирлянде?

102
Вариант 7
1. Решить задачу, используя диаграмму Эйлера-Венна.
Каждый из студентов группы занимается хотя бы одним видом спорта.
Пятеро занимаются альпинизмом, шестеро – волейболом, 10 человек – борь-
бой. Известно, что двое занимаются и альпинизмом, и волейболом; трое – во-
лейболом и борьбой; четверо – альпинизмом и борьбой; а один занимается
всеми тремя видами спорта. Сколько студентов занимается только борьбой?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
6
,
5
,
4
{
},
6
,
4
,
3
,
2
,
1
{
},
8
,
7
,
5
,
4
,
2
{
=
=
=
Z
Y
X
. Найти булеан множества
Z
и какое-либо разбиение множества
Y
. Выполнить действия
)
(
\
Y
Z
X
∩
.
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
.
)
(
)
(
B
C
B
B
B
A
A
∪
∪
∩
∪
∪
∩
4. Пусть
}
4
,
3
,
2
,
1
,
0
{
=
X
. Бинарное отношение
X
X
R
×
⊆
задано ха-
рактеристическим свойством:
}
,
,
3
на
делится
)
,
{(
X
b
a
b
a
b
a
R
∈
+
=
.
Представить отношение
R
другими возможными способами. Какими
свойствами обладает это отношение? Является ли оно отношением эквива-
лентности?
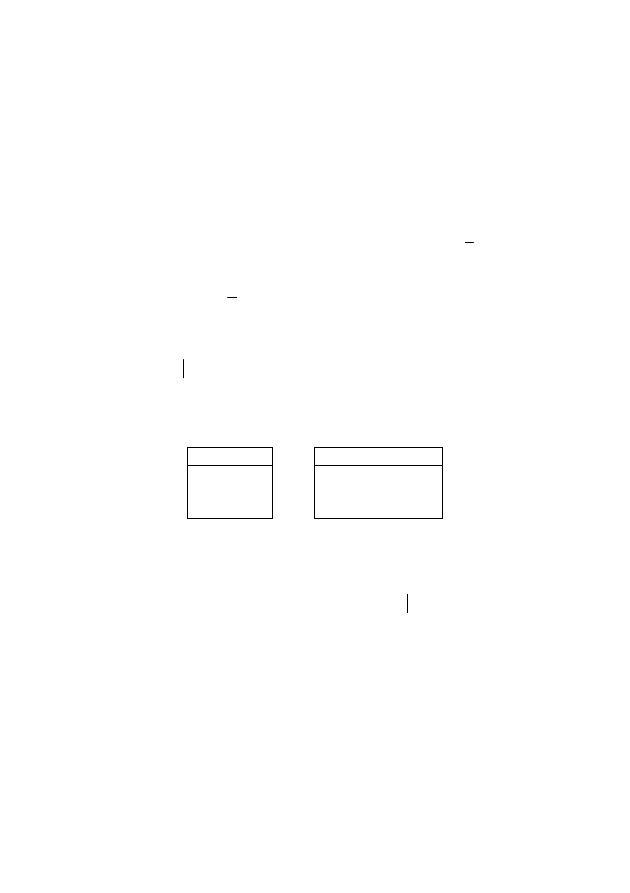
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
B
3
a
e d a b c
a b c b e d
d a b d e c
Записать обозначения операций реляционной алгебры и выполнить их:
а) селекция отношения
R
по условию “
2
1
A
A
>
”;
б) проекция на список (2,3) объединения отношений
R
и
S
.
6. Даны множества
}
4
,
2
,
0
{
=
A
и
∈
=
n
n
B
4
{
N
}. Какова мощность
множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. В магазине продается восемь типов шляп. Сколькими способами дама
может выбрать себе три разных шляпы?
8. В библиотеке на полке стоит три одинаковых учебника по математике
и четыре разных по программированию. Сколькими способами их можно рас-
ставить на полке?
103
Вариант 8
1. Решить задачу, используя диаграмму Эйлера-Венна.
В одной из студенческих групп все студенты умеют программировать.
Десять человек умеют работать на Бейсике, 10 – на Паскале, 6 – на Си. Два
языка знают: 6 человек Бейсик и Паскаль, 4 – Паскаль и Си, 3 – Бейсик и Си.
Один человек знает все три языка. Сколько студентов в группе?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
7
,
4
,
1
{
},
8
,
7
,
5
,
3
,
2
{
},
7
,
6
,
4
,
2
,
1
{
=
=
=
Z
Y
X
. Найти булеан множества
Z
и какое-либо разбиение множества
Y
. Выполнить действия
Z
Y
X
∩
∪
)
(
.
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
.
)
)
)
(((
B
A
B
B
A
∪
∩
∪
∩
4. Пусть
}
4
,
3
,
2
,
1
{
=
X
. Бинарное отношение
X
X
R
×
⊆
задано харак-
теристическим свойством:
}
,
,
4
)
,
{(
X
b
a
b
a
b
a
R
∈
<
+
=
.
Представить отношение
R
другими возможными способами. Выяснить,
какими свойствами оно обладает.
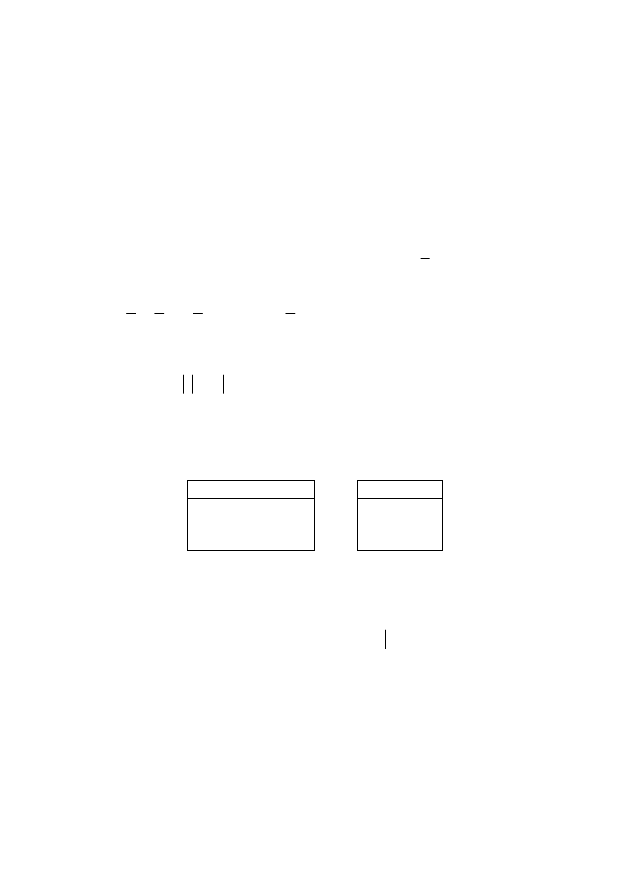
5. Заданы отношения:
R: S:
A
1
A
2
B
1
B
2
B
3
x
y
u
t
v
y z x z y
x t y z v
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция на список (2,1) отношения
S
;
б) соединение отношений
R
и
S
по условию “
2
1
B
A
<
”.
6. Даны множества
}
6
,
4
,
2
{
=
A
и
∈
−
=
n
n
B
3
5
{
N
}. Какова мощ-
ность множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. В сессию студент сдает пять экзаменов. Сколько возможных результа-
тов сессии (экзаменационной оценкой может быть 2,3,4,5)?
8. Сколькими способами 12 книг можно расставить по трем полкам, если
на каждой полке могут поместиться все книги? Способы различаются лишь
количеством книг на полках.
104
Вариант 9
1. Решить задачу, используя диаграмму Эйлера-Венна.
При изучении читательского спроса оказалось, что 60% опрошенных чи-
тает журнал “Огонек”, 50% - журнал “Юность”, 50% - журнал “Аврора”. Жур-
налы “Огонек” и “Юность” читают 30% опрошенных, “Юность” и “Аврора” –
20%, “Огонек” и “Аврора” – 40%, все три журнала – 10%. Сколько процентов
опрошенных не читают ни один журнал?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
8
,
7
,
5
,
2
{
},
8
,
4
,
2
,
1
{
},
7
,
5
,
4
,
3
,
2
{
=
=
=
Z
Y
X
. Найти булеан множества Y и
какое-либо разбиение множества
X
. Выполнить действия
).
(
\
Y
X
Z
∩
3. Доказать, используя законы и тождества алгебры множеств (перечис-
лить используемые законы):
.
)
(
)
(
)
(
U
B
A
B
A
B
A
=
∪
∪
∩
∪
∩
4. Пусть
}
5
,
4
,
3
,
2
,
1
{
=
X
. Отношение
X
X
R
×
⊆
задано характери-
стическим свойством:
}
,
,
2
)
,
{(
X
b
a
b
a
b
a
R
∈
=
−
=
.
Представить отношение
R
другими возможными способами. Выяснить,
какими свойствами оно обладает. Является ли
R
отношением эквивалентно-
сти?
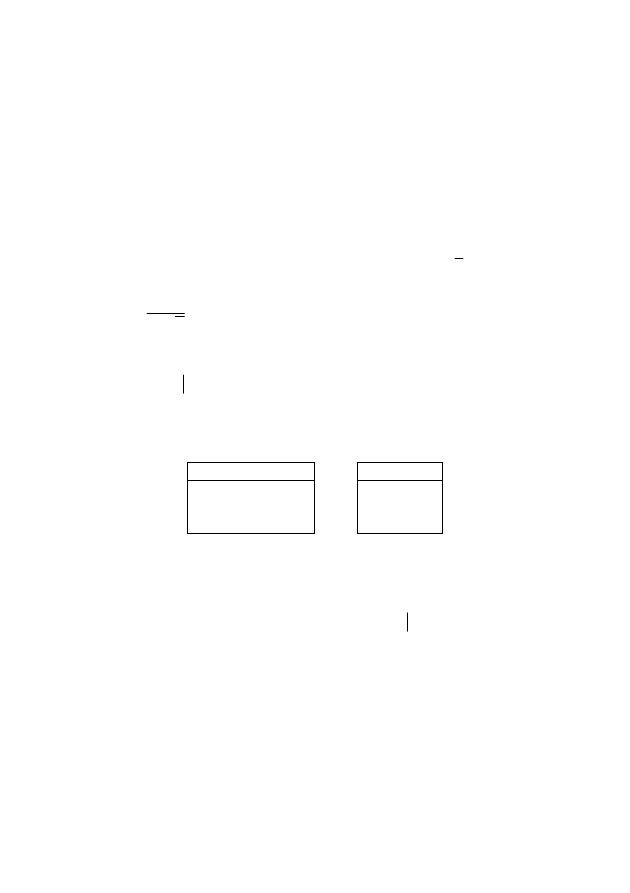
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
a
d e d e
d c b d c
b d a a c
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция на список (2,1) отношения
R
;
б) соединение отношений
R
и
S
по условию “
1
1
B
A
≥
”.
6. Даны множества
}
6
,
4
,
2
,
1
{
=
A
и
∈
=
n
n
B
2
{
N
}. Какова мощность
множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. На столе лежат восемь яблок. Сколькими способами можно выбрать
два из них?
8. Требуется покрасить шесть гаражей, стоящих в один ряд. На каждый
из гаражей расходуется одна банка краски. Сколькими способами можно по-
красить гаражи, если есть две банки красной краски, три зеленой и одна си-
ней?
105
Вариант 10
1. Решить задачу, используя диаграмму Эйлера-Венна.
В день авиации всех желающих катали на самолете, планере, дельта-
плане. На самолете прокатилось 30 человек, на планере – 20, на дельтаплане –
15. И на самолете, и на планере каталось 10 человек, на самолете и дельта-
плане – 12, на планере и дельтаплане – 5, два человека прокатились и на само-
лете, и на планере, и на дельтаплане. Сколько было желающих прокатиться?
2. Задано универсальное множество
}
8
,
7
,
6
,
5
,
4
,
3
,
2
,
1
{
=
U
и множества
}
6
,
5
,
3
,
1
{
},
8
,
6
,
5
,
2
{
},
8
,
7
,
5
,
3
,
1
{
=
=
=
Z
Y
X
. Найти булеан множества
Z
и
какое-либо разбиение множества
Y
. Выполнить действия
Z
Y
X
∪
∩ )
(
.
3. Упростить, используя законы и тождества алгебры множеств (пере-
числить используемые законы):
.
U
B
A
A
∩
∪
∪
4. Пусть
}
5
,
4
,
3
,
2
,
1
{
=
X
. Бинарное отношение
X
X
R
×
⊆
задано ха-
рактеристическим свойством:
}
,
,
1
)
,
{(
X
b
a
b
a
b
a
R
∈
>
−
=
.
Представить отношение
R
другими возможными способами. Выяснить,
какими свойствами оно обладает.
5. Заданы отношения:
R: S:
A
1
A
2
A
3
B
1
B
2
a
b c b e
a c d b c
b c d d c
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция на список (3,2) отношения
R
;
б) соединение отношений
R
и
S
по условию “
1
1
B
A
=
”.
6. Даны множества
}
4
,
3
,
2
,
1
{
=
A
и
∈
−
=
n
n
B
1
{
2
N
} . Какова мощ-
ность множеств
B
A
B
A
B
A
×
∪
∩
,
,
?
7. Сколькими способами 8 человек можно рассадить на лавке (всех в
один ряд)?
8. Восемь туристов отправились в путь на двух лодках, в меньшей из ко-
торых могли поместиться не более четверых, а в большей – не более шестерых
человек. Сколькими различными способами они могут распределиться в раз-
ные лодки? (Распределения считаются различными, если хотя бы один турист
окажется в другой лодке).