ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9335
Скачиваний: 24

116
9
ГРАФЫ
9.1
Определение
графа
Понятие
графа
опирается
на
понятие
множества
.
Графиче
-
ски
задается
множество
и
элементы
множества
,
находящиеся
ме
-
жду
собой
в
некотором
отношении
.
При
проектировании
конструкций
пользователю
удобнее
иметь
дело
с
моделями
,
которые
легко
образуются
,
если
элемен
-
ты
конструкций
принять
за
точки
,
а
связи
между
ними
принять
за
линии
.
Объект
,
состоящий
из
двух
множеств
(
множества
точек
и
множества
линий
),
которые
находятся
между
собой
в
некотором
отношении
,
называется
графом.
Точки
обозначают
Х
= {
х
1
,
х
2
,…,
х
n
}, |
Х
| = n
и
называют
вершинами
графа
.
Множество
линий
,
соединяющих
пары
вершин
(x
i
,
х
j
),
где
x
i
,
х
j
∈
Х
,
называется
множеством ребер или дуг,
и
обозначается
U = {u
1
, u
2
,…, u
m
}, |U| = m.
Графом
можно
считать
объект
,
который
обозначается
как
G = (X, U).
В
общем
случае
множество
линий
U
можно
представить
в
виде
U =
Ũ
∪
Ū
∪
Ů
,
где
Ũ
–
подмножество
неориентированных
линий
(ребер),
в
кото
-
ром
каждое
ребро
u
i
≈ ∈
Ũ
определяется
неупорядоченной
парой
вершин
x
i
,
х
j
,
которые
оно
соединяет
,
и
записывается
u
k
= (x
i
,
х
j
),
или
u
k
= (
х
j
, x
i
).
Ū
–
подмножество
ориентированных
линий
(дуг).
Существенно
направление
соединений
.
Каждая
дуга
u
i
∈
Ū
определяется
упорядоченной
парой
вершин
x
i
,
х
j
,
которые
u
k
со
-
единяет
,
и
записывается
u
k
= < x
i
,
х
j
>.
Ů
–
подмножество
линий
(
петель
),
каждая
из
которых
выхо
-
дит
и
входит
в
одну
и
ту
же
соответствующую
этой
линии
вер
-
шину
.
Каждая
петля
определяется
упорядоченной
или
неупоря
-
доченной
парой
u
i
= (x
k
,
х
k
)
или
u
i
= < x
k
,
х
k
>.
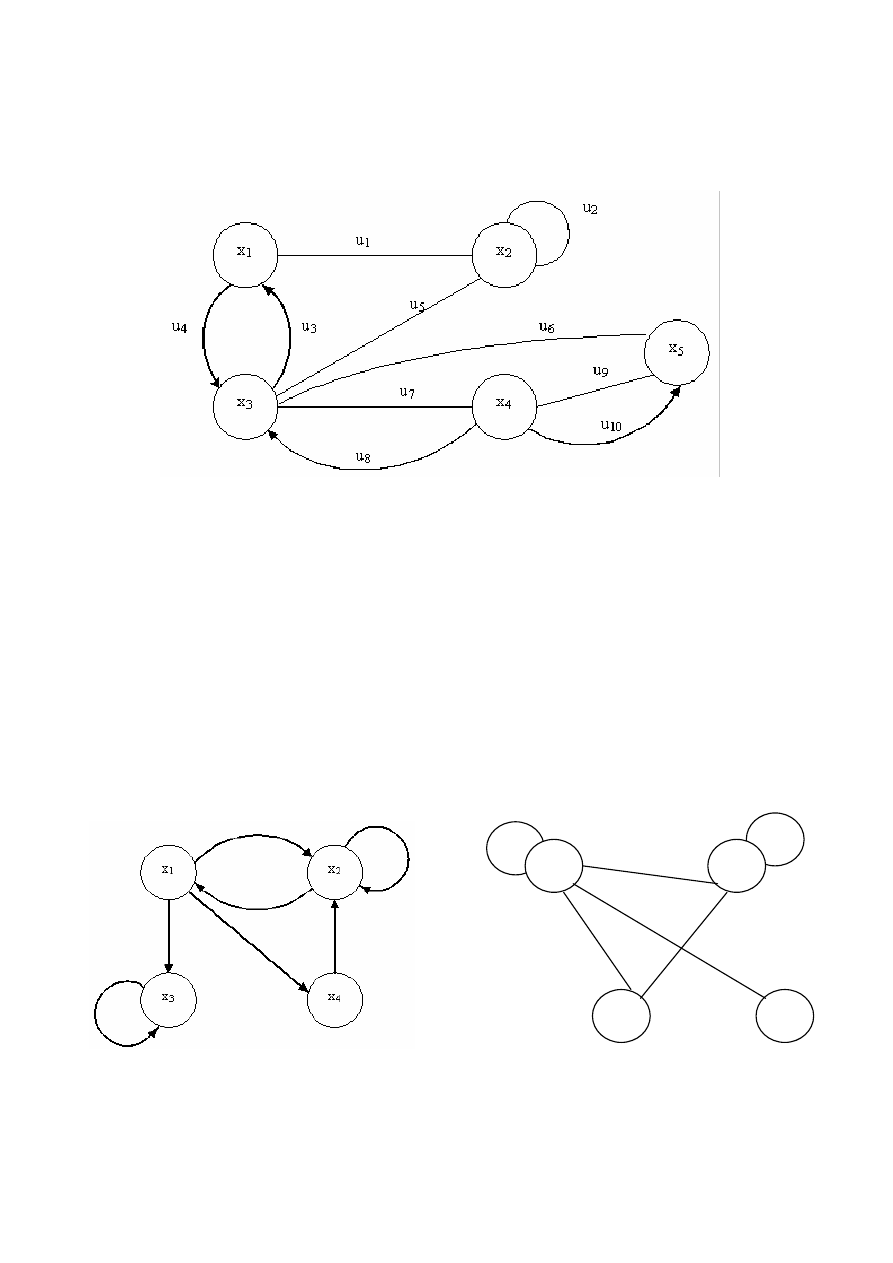
117
Граф
G = (X, U),
у
которого
Ū
,
Ũ
,
Ů
≠ ∅,
называется
сме-
шанным.
Рисунок 9.1
Здесь
|
Х
| = 5; |U| = 13; U =
Ũ
∪
Ū
∪
Ů
;
Ū
= {u
3
, u
4
, u
7
, u
8
, u
10
};
Ũ
= {u
1
, u
5
, u
6
, u
9
};
Ů
= {u
2
}.
Подмножество
U
можно
представить
как
множество
корте
-
жей
длины
2.
Граф
G = (X, U),
у
которого
U =
Ů
∪
Ū
,
а
Ũ
= Ø,
называется
ориентированным
графом
,
или
орграфом.
Граф
G = (X, U),
у
которого
U =
Ũ
∪
Ů
,
называется
неориен-
тированным,
или
неорграфом.
Рисунок 9.2 – Орграф с петлями Рисунок 9.3 – Неорграф с петлями
х
4
х
3
х
2
х
1
118
На
рисунке
9.2
показан
орграф
с
петлями
,
где
u = {<x
1
, x
2
>,
<x
2
, x
1
>, <x
2
, x
2
>, <x
1
, x
4
>, <x
1
, x
3
>, <x
4
, x
2
>, <x
3
, x
3
>}.
Каждая
ду
-
га
u
i
∈U
z
представляется
парой
соединяемых
вершин
,
причем
первой
в
кортеже
стоит
вершина
,
из
которой
дуга
выходит
,
а
вто
-
рой
–
вершина
,
в
которую
дуга
входит
.
На
рисунке
9.3
приведен
пример
неорграфа
с
петлями
.
В
дальнейшем
неорграфы
будем
называть
просто
графами
.
Граф
G = (X, U),
у
которого
существует
хотя
бы
одна
пара
вершин
,
соединяемых
m
ребрами
(m>1) u
i
∈U,
называется
муль-
тиграфом,
а
максимальное
значение
m
называется
мультигра-
фическим числом
графа
G.
Ребра
,
соединяющие
одну
и
ту
же
па
-
ру
вершин
,
называются
кратными
.
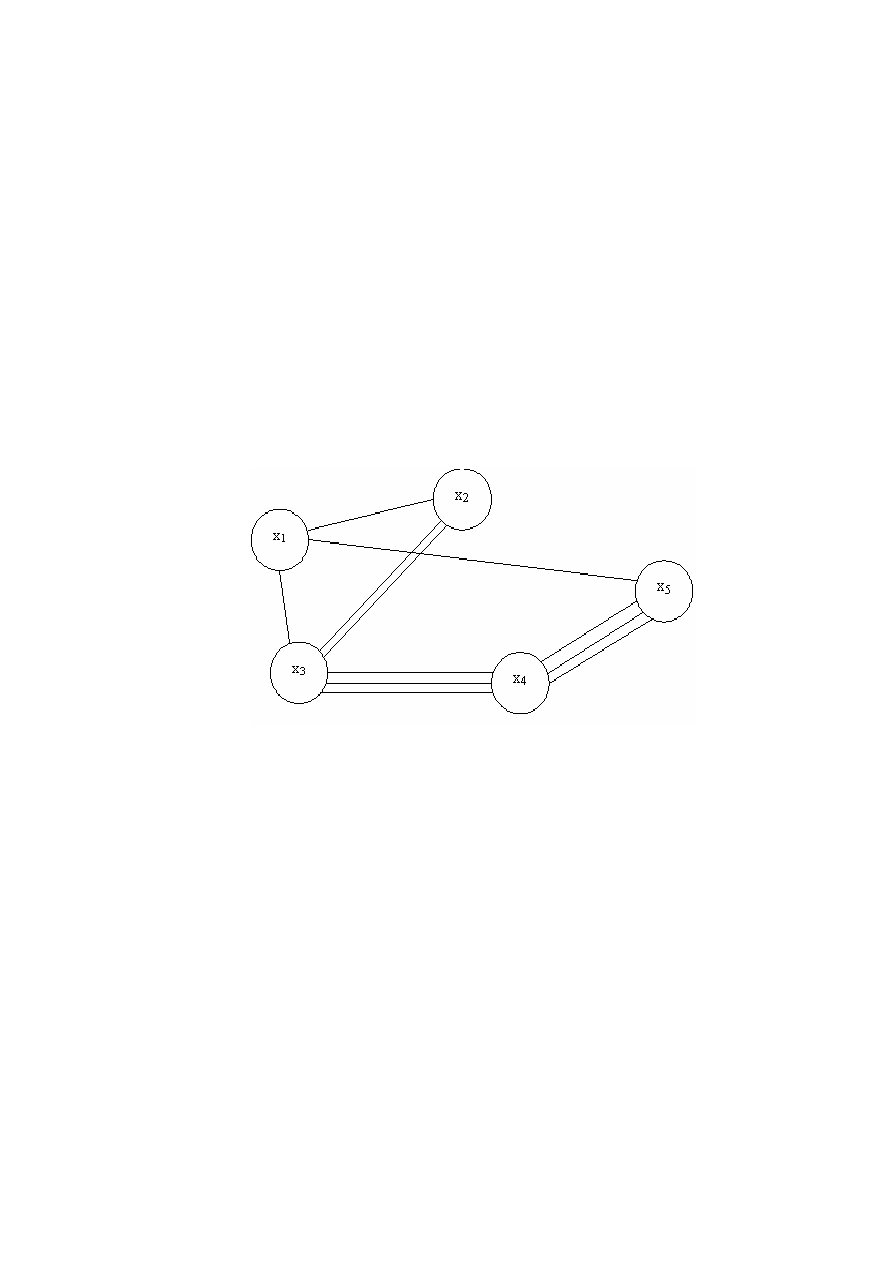
Пример
мультиграфа
приве
-
ден
на
рисунке
9.4.
Рисунок 9.4 – Мультиграф
Мультиграфическое
число
графа
,
приведенного
в
качестве
примера
,
равно
m = 3.
9.2
Задание
графов
Если
ребро
u
k
∈U
графа
G = (X, U)
соединяет
вершины
x
i
,
x
j
∈X,
т
.
е
. u
k
= (x
i
, x
j
),
то
говорят
,
что
ребро
u
k
инцидентно
вер
-
шинам
x
i
, x
j
.
Вершины
x
i
, x
j
называют
инцидентными
ребру
u
k
.
Любые
две
вершины
x
i
, x
j
∈X
графа
G = (X, U)
называют
смежными
,
если
существует
соединяющее
эти
вершины
ребро
u
k
∈U,
т
.
е
. u
k
= (x
i
, x
j
).
Если
два
ребра
инцидентны
одной
и
той
же
вершине
,
то
их
называют
смежными
.
119
Отношения
смежности
и
инцидентности
могут
иметь
место
как
на
множестве
Х
,
так
и
на
множестве
U.
Основными
способами
задания
графов
являются
геометри
-
ческий
,
аналитический
и
матричный
.
Граф
называется
помеченным,
если
его
вершины
отличают
-
ся
одна
от
другой
метками
.
Например
,
х
1
,
х
2
,
х
3
,…,
х
n
.
Говорят
,
что
задан граф,
если
заданы
множество
вершин
Х
,
множество
ребер
U
и
инцидентор
F,
определяющий
,
какую
пару
вершин
x
i
, x
j
∈X
соединяет
ребро
u
k
= (x
i
, x
j
).
Большинство
задач
автоматизации
конструирования
реша
-
ется
при
помощи
матричного
задания
графа
.
Квадратную
таблицу
R =
||r
ij
||
nyn
называют
матрицей
смеж
-
ности
,
если
ее
элементы
образуются
по
правилу
:
1,
если
вершина
x
i
смежна
с
x
j
;
r
ij
=
0,
в
противном
случае
.
Для
мультиграфа
запишется
:
m,
если
вершина
x
i
соединена
с
вершиной
x
j
m
ребрами
;
r
ij
=
0,
в
противном
случае
.
При
таком
задании
очевидно
,
что
матрица
будет
симмет
-
ричной
.
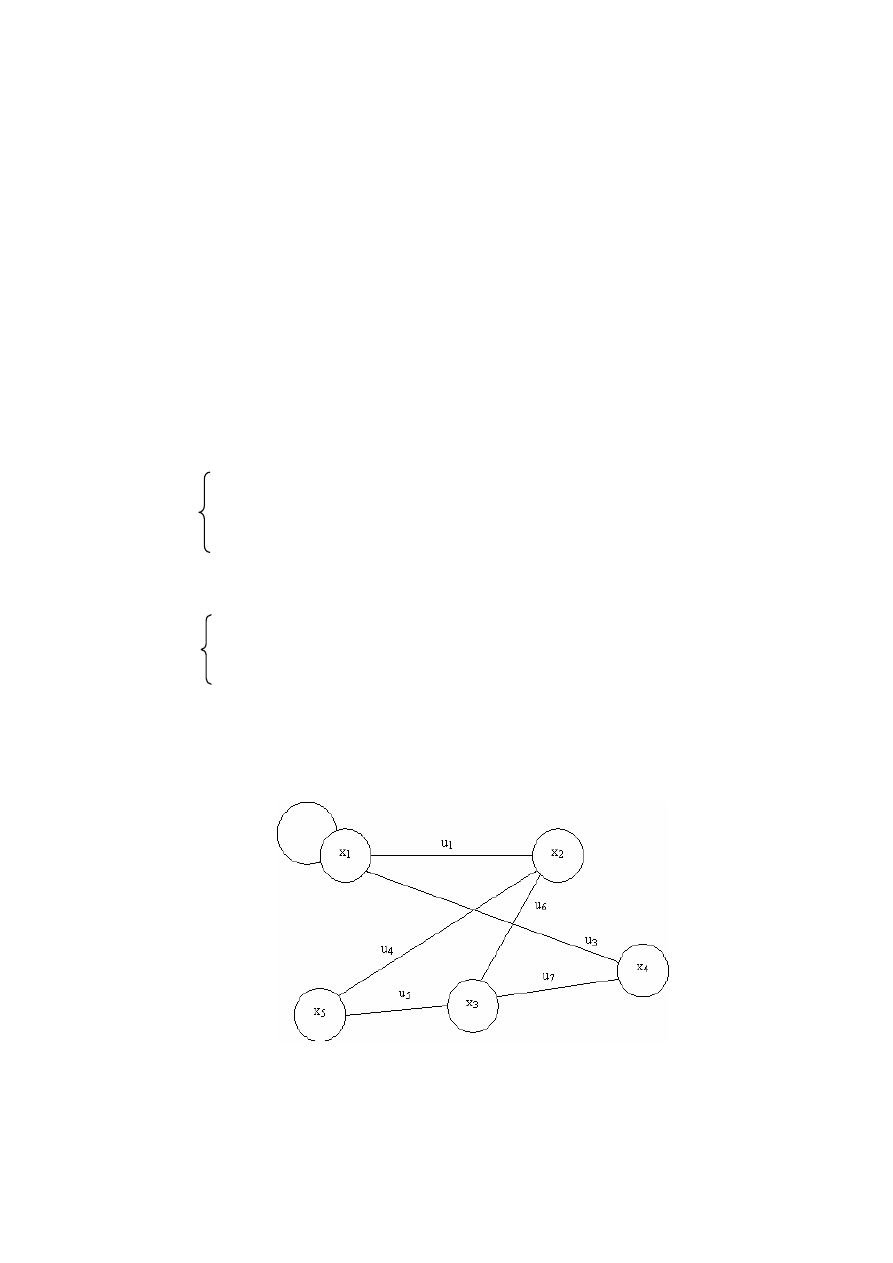
Рисунок 9.5 Пример графа

120
Матрица
смежности
R
будет
выглядеть
:
х
1
х
2
х
3
х
4
х
5
х
1
1 1 0 1 0
х
2
1 0 1 0 1
х
3
0 1 0 1 1
х
4
1 0 1 0 0
х
5
0 1 1 0 0
Недостаток
этого
представления
состоит
в
том
,
что
объем
занимаемой
памяти
составляет
n
2
.
Объем
памяти
можно
сокра
-
тить
,
если
хранить
треугольную
матрицу
:
х
1
х
2
х
3
х
4
х
5
х
1
1 1 0 1 0
х
2
0 1 0 1
х
3
0 1 1
х
4
0
0
х
5
0
в
том
случае
,
когда
в
графе
G = (X, U) |X| = n, |U| = m m<<n,
его
задают
с
помощью
списка
пар
,
соответствующих
его
ребрам
или
с
помощью
списков
смежности
.
Для
рисунка
7.5
список
пар
вы
-
глядит
: 1 1, 1 2, 1 4, 2 5, 2 3, 3 4, 3 5.
Объем
памяти
составит
2m.
При
таком
представлении
нетрудно
найти
все
ребра
,
ведущие
из
одной
вершины
.
При
представлении
графа
списком
смежности
для
каждой
вершины
x
i
∈X
составляется
список
вершин
x
j
,
таких
,
что
(x
i
, x
j
)
∈U.
Для
графа
,
приведенного
на
рисунке
7.5,
списки
смежности
выглядят
: