ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9332
Скачиваний: 24
126
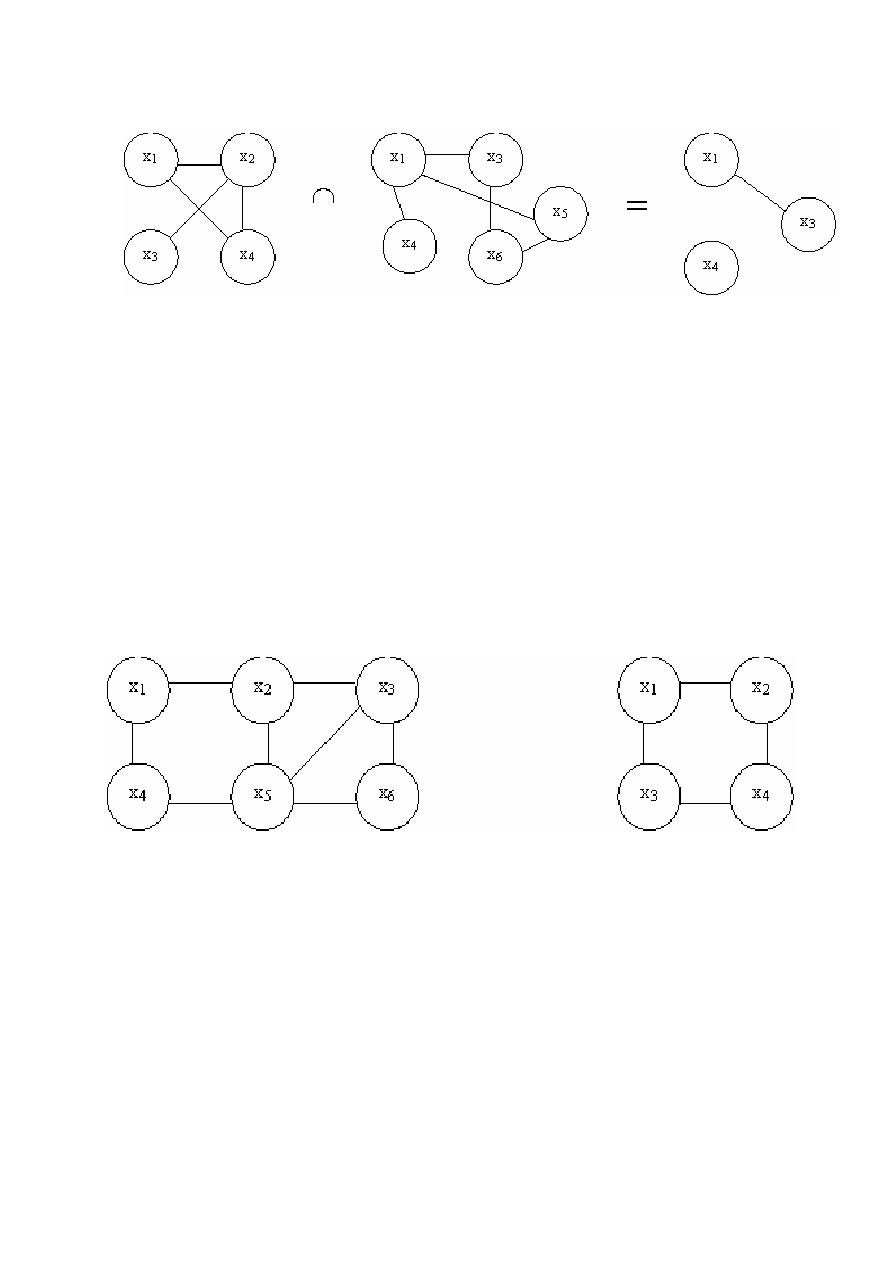
Рисунок 9.12
− Пример пересечения
9.3
Связность
графа
Маршрутом
в
графе
G=(X, U)
называют
некоторую
конеч
-
ную
последовательность
ребер
вида
s=(x
0
, x
1
)(x
1
, x
2
),…, (x
l–1
, x
l
),
где
х
0
,
х
2
–
начальная
и
конечная
вершины
,
соответственно
.
Чис
-
ло
ребер
в
маршруте
называется
его
длиной.
Маршрут
,
в
котором
нет
повторяющихся
ребер
,
называют
цепью.
Если
в
маршруте
различны
все
вершины
,
то
он
называет
-
ся
простой цепью.
Замкнутая
цепь
,
у
которой
начальная
и
ко
-
нечная
вершины
совпадают
х
0
=
х
l
,
называется
циклом.
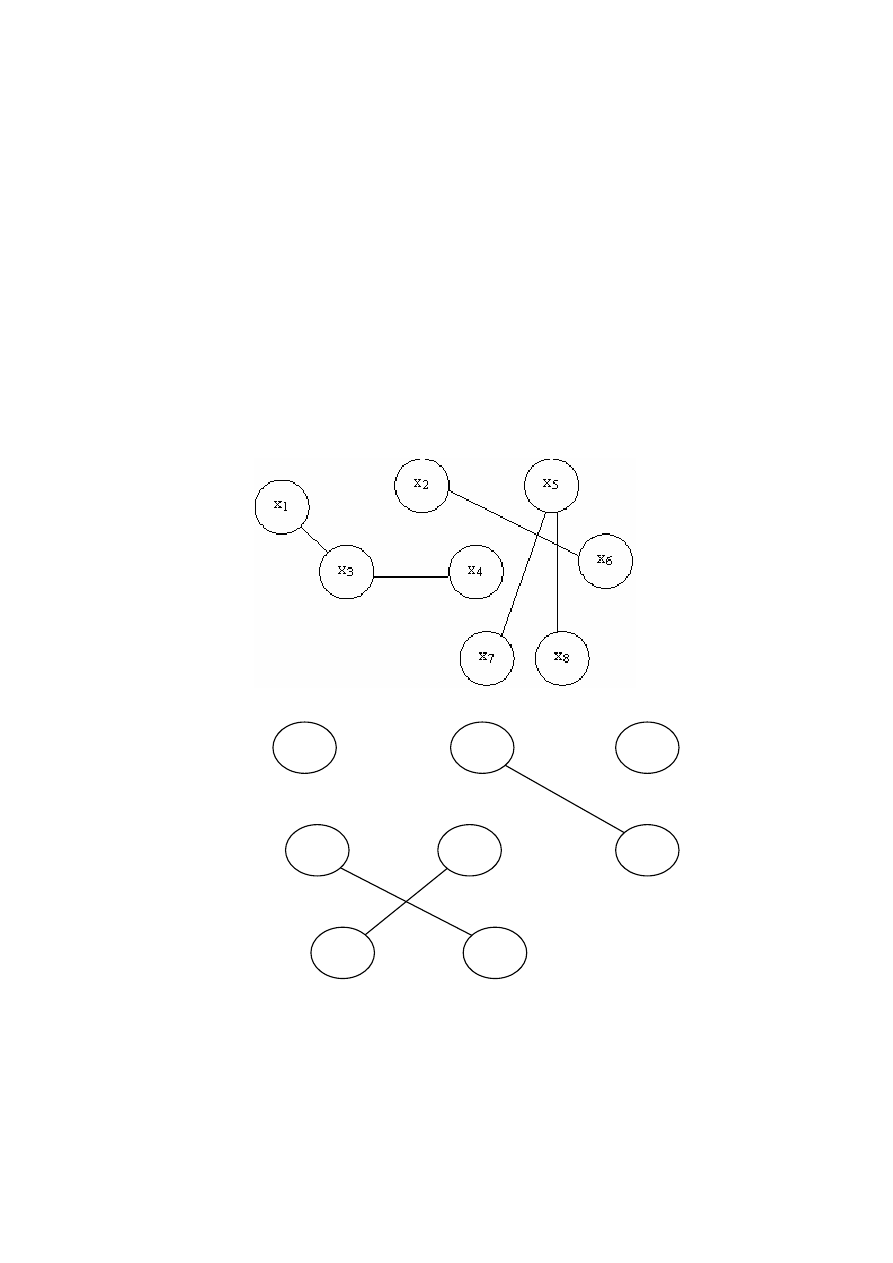
Рисунок 9.13
− Граф G Рисунок 9.14 − Граф
На
рисунке
9.13
в
графе
G
построим
маршрут
,
цепь
и
цикл
.
S
1
= (x
1
,x
2
)(x
2
,x
3
)(x
3
,x
5
)(x
5
,x
2
)(x
2
,x
1
)(x
1
,x
4
) –
маршрут
;
S
2
= (x
1
,x
2
)(x
2
,x
3
)(x
3
,x
5
)(x
5
,x
2
) –
цепь
;
S
3
= (x
5
,x
2
)(x
2
,x
3
)(x
3
,x
6
)(x
6
,x
5
) –
цикл
;
S
4
= (x
4
,x
5
)(x
5
, x
3
)(x
3
,x
6
) –
простая
цепь
.
Существует
простой
способ
определения
существования
маршрутов
длины
q
по
матрице
R
графа
G
путем
возведения
ее
в
q
степень
.

127
Пусть
задана
матрица
смежности
R
графа
,
изображенного
на
рисунке
9.14.
R=
R
2
=
Каждый
элемент
в
матрице
R
2
равен
числу
маршрутов
,
ве
-
дущих
из
вершины
х
i
в
вершину
х
j
.
Например
, r
3,2
= 2
указывает
,
что
существуют
два
маршрута
длины
2
из
вершины
x
3
в
вершину
x
2
. s
1
= (x
3
,x
1
)(x
1
, x
2
); s
2
= (x
3
, x
4
)(x
4
, x
2
). (
Возведение
матрицы
в
степень
производится
по
правилу
умножения
матриц
).
Для
опре
-
деления
числа
маршрутов
длины
З
необходимо
определить
мат
-
рицу
R
3
.
R
3
=
s
1
= (x
1
, x
2
)(x
2
, x
1
)(x
1
, x
2
);
s
2
= (x
1
, x
3
)(x
3
, x
1
)(x
4
, x
2
);
s
3
= (x
1
, x
2
)(x
2
, x
4
)(x
4
, x
2
); s
4
= (x
1
, x
3
)(x
3
, x
1
)(x
1
, x
2
).
Понятие
связности
графов
относится
к
одному
из
наиболее
важных
понятий
теории
графов
.
Две
произвольные
вершины
x
i
, x
j
∈X
графа
G=(X, U)
назы
-
ваются
связными,
если
существует
маршрут
5,
в
котором
вер
-
шины
x
i
, x
j
будут
концевыми
.
Граф
называется
связным,
если
любые
две
его
вершины
связны
,
т
.
е
. 2
вершины
объединены
про
-
стой
цепью
.
В
противном
случае
граф
не
связан
,
а
каждый
из
со
-
ставляющих
его
связных
подграфов
G
1
, G
2
,…, G
e
называется
компонентой связности.
Из
определения
связности
следует
:
o
в
связном
графе
вершина
x
i
связана
сама
с
собой
(
рефлек
-
сивность
);
1 2 3 4
1 0 1 1 0
2 1 0 0 1
3 1 0 0 1
4 0 1 1 0
1 2 3
4
1 2 0 0 2
2 0 2 2 0
3 0 2 2 0
4 2 0 0 2
1 2 3 4
1 0 4 4 0
2 4 0 0 4
3 4 0 0 4
4 0 4 4 0
r
1,2
=4,
показывает
,
что
суще
-
ствует
4
маршрута
длины
3,
веду
-
щие
из
вершины
х
1
в
х
2
.
128
o
если
вершина
x
i
связана
с
вершиной
x
j
,
то
x
j
связана
с
x
i
(
симметричность
);
o
если
x
i
связана
с
x
j
и
x
j
связана
с
х
k
,
то
x
i
связана
с
х
k
(x
i
,
x
j
,
х
k
∈X) (
транзитивность
),
из
чего
следует
,
что
отношение
связ
-
ности
является
отношением
эквивалентности
.
В
этом
случае
множество
вершин
графа
G=(X, U),
который
моделирует
схему
,
можно
разбить
на
непересекающиеся
классы
Х
i
,
причем
ребра
графа
будут
соединять
только
вершины
внутри
этих
классов
.
Число
компонент
,
из
которых
состоит
граф
,
назы
-
вается
степенью связности.
Связный
граф
состоит
из
одной
компоненты
связности
.
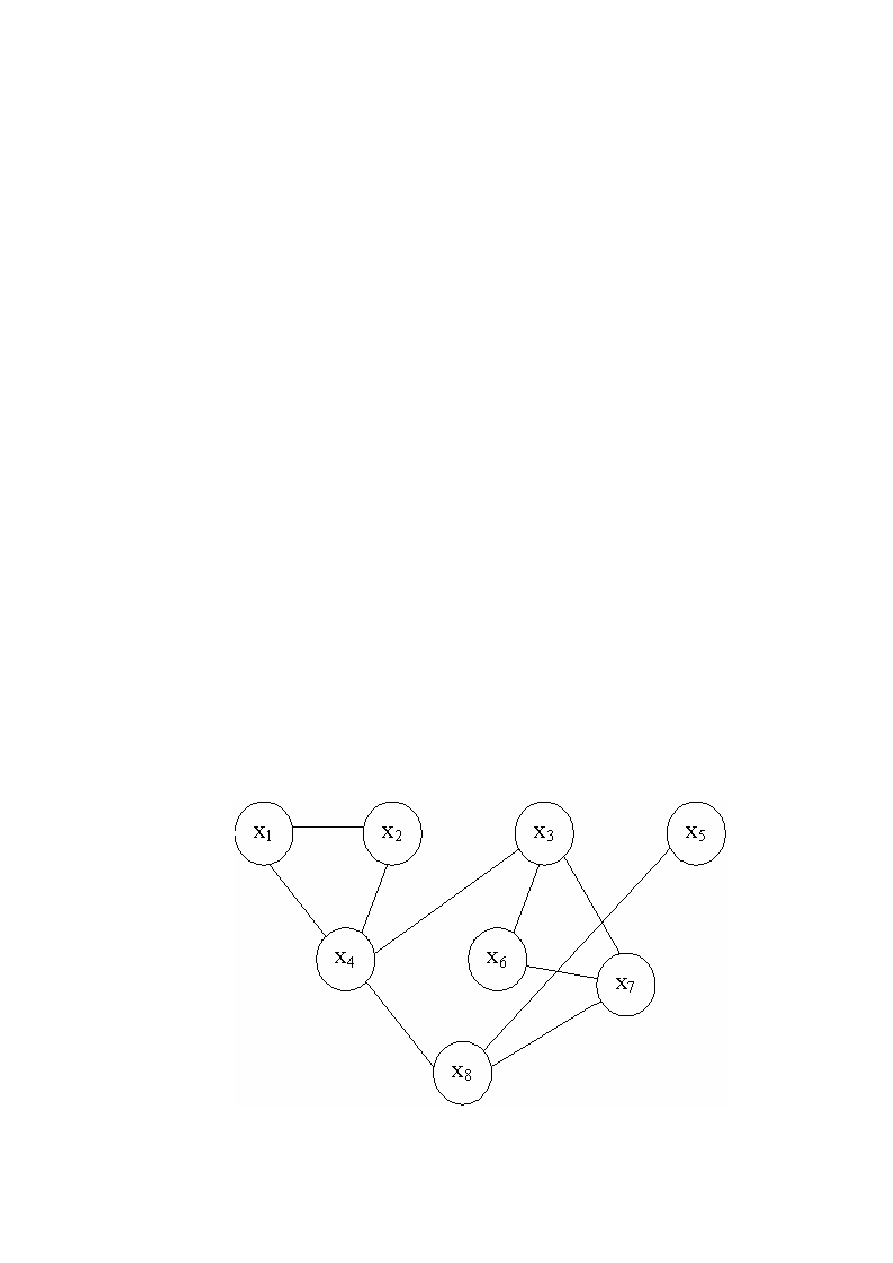
Примеры
графов
,
состоящих
из
несколь
-
ких
компонент
связности
,
приведены
на
рисунке
9.15.
а)
б)
Рисунок 9.15
− Граф, состоящий из трех компонент связности (а),
из пяти компонент связности (б)
х
1
х
2
х
4
х
5
х
7
х
8
х
6
х
3
129
Одной
из
характеристик
связных
графов
является
число
ре
-
бер
в
графе
с
n
вершинами
и
заданным
числом
k
компонент
связ
-
ности
.
Число
ребер
удовлетворяет
неравенству
:
n – k
≤ m ≤ (n – k)(n – k – 1)/2.
Граф
с
n
вершинами
,
содержащий
более
чем
(n–1)(n–2)/2
ребер
,
связан
.
Нахождение простых цепей
Необходимо
найти
все
простые
цепи
графа
G,
соединяющие
две
произвольные
вершины
.
Граф
может
быть
связан
,
а
может
быть
не
связан
.
Если
вершины
принадлежат
одной
компоненте
связности
,
то
решение
можно
найти
.
Если
вершины
принадлежат
разным
компонентам
связности
,
то
решения
нет
.
Алгоритм
нахождения
простых
цепей
из
вершины
i
в
вер
-
шину
j
состоит
из
следующих
шагов
:
1.
Выбрать
вершину
i.
2.
Для
выбранной
вершины
составить
список
смежных
вершин
таких
,
каких
не
было
в
цепи
.
3.
Проверить
есть
ли
среди
них
искомая
вершина
.
4.
Если
есть
искомая
вершина
–
записать
цепь
отдельно
.
5.
Для
остальных
вершин
(
для
каждой
из
вершин
)
перейти
к
п
.2.
Цикл
необходимо
выполнить
n–1
раз
для
связного
графа
.
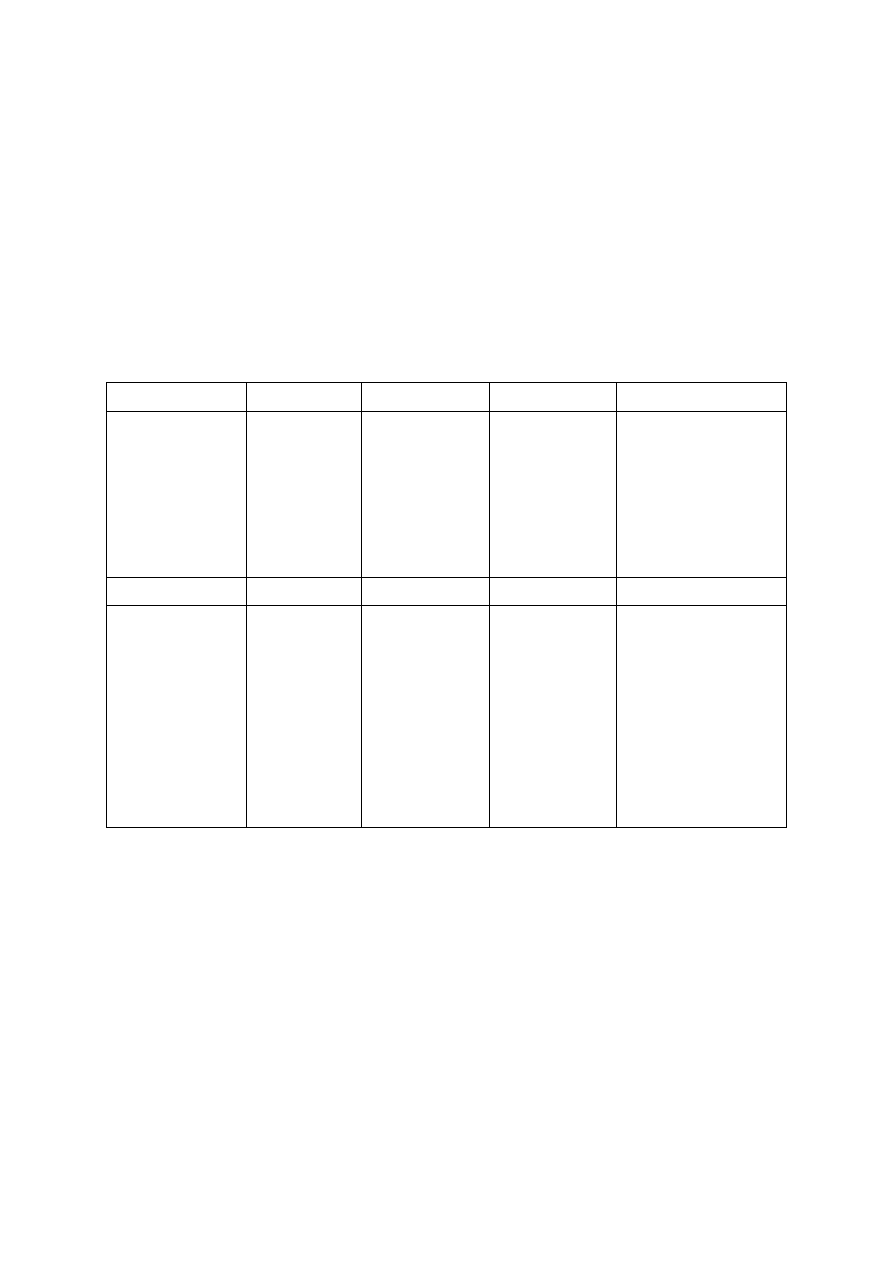
Рассмотрим
пример
нахождения
простых
цепей
для
графа
,
приведенного
на
рисунке
9.16.
Построим
все
простые
цепи
из
вершины
x
1
в
вершину
x
7
.
Рисунок 9.16
130
Для
поиска
в
ширину
на
первом
шаге
строим
простые
цепи
1-2
и
1-4.
На
втором
шаге
выбираем
вершину
2
в
качестве
исход
-
ной
и
рассматриваем
все
смежные
с
ней
вершины
.
С
ней
смежны
вершины
1
и
4,
но
вершина
1
уже
присутствует
в
цепи
,
поэтому
полученная
цепь
будет
1-2-4.
Для
вершины
4
получим
цепи
1-4-
2, 1-4-3, 1-4-8.
На
третьем
шаге
необходимо
обратить
внимание
на
то
,
что
цепь
1-4-2
тупиковая
,
поскольку
все
вершины
,
смеж
-
ные
с
вершиной
2,
а
это
вершины
2
и
4,
уже
присутствуют
в
цепи
.
Шаг
1
Шаг
2
Шаг
3
Шаг
4
Шаг
5
1-2
1-4
1-2-4
1-4-2
1-4-3
1-4-8
1-2-4-3
1-2-4-8
1-4-3-7
1-4-3-5
1-4-8-7
1-4-8-6
1-2-4-3-7
1-2-4-3-5
1-2-4-8-7
1-2-4-8-6
1-4-3-5-7
1-2-4-3-5-7
Либо
1-2
1-4
1-2-4
1-4-3
1-4-8
1-2-4-3
1-2-4-8
1-4-3-7
1-4-3-7
1-4-8-6
1-4-8-7
1-2-4-3-5
1-2-4-3-7
1-2-4-8-6
1-2-4-8-7
1-4-3-5
тупик
1-2-4-3-5-7
тупик
1-4-3-5-7
Пусть
задан
связный
граф
G=(X, U).
Подмножество
U’
⊆U
называется
разделяющим,
если
после
его
удаления
граф
стано
-
вится
несвязным
.
Разделяющее
подмножество
всегда
существу
-
ет
.
Если
разделяющее
множество
состоит
из
одного
ребра
u
i
∈U,
то
u
i
называется
перешейком
или
мостом.
Ребра
(x
3
,x
4
) (x
4
,x
7
)
графа
,
приведенного
на
рисунке
9.17,
являются
перешейком
.