Файл: Дискретная мат-ка_УП.pdf

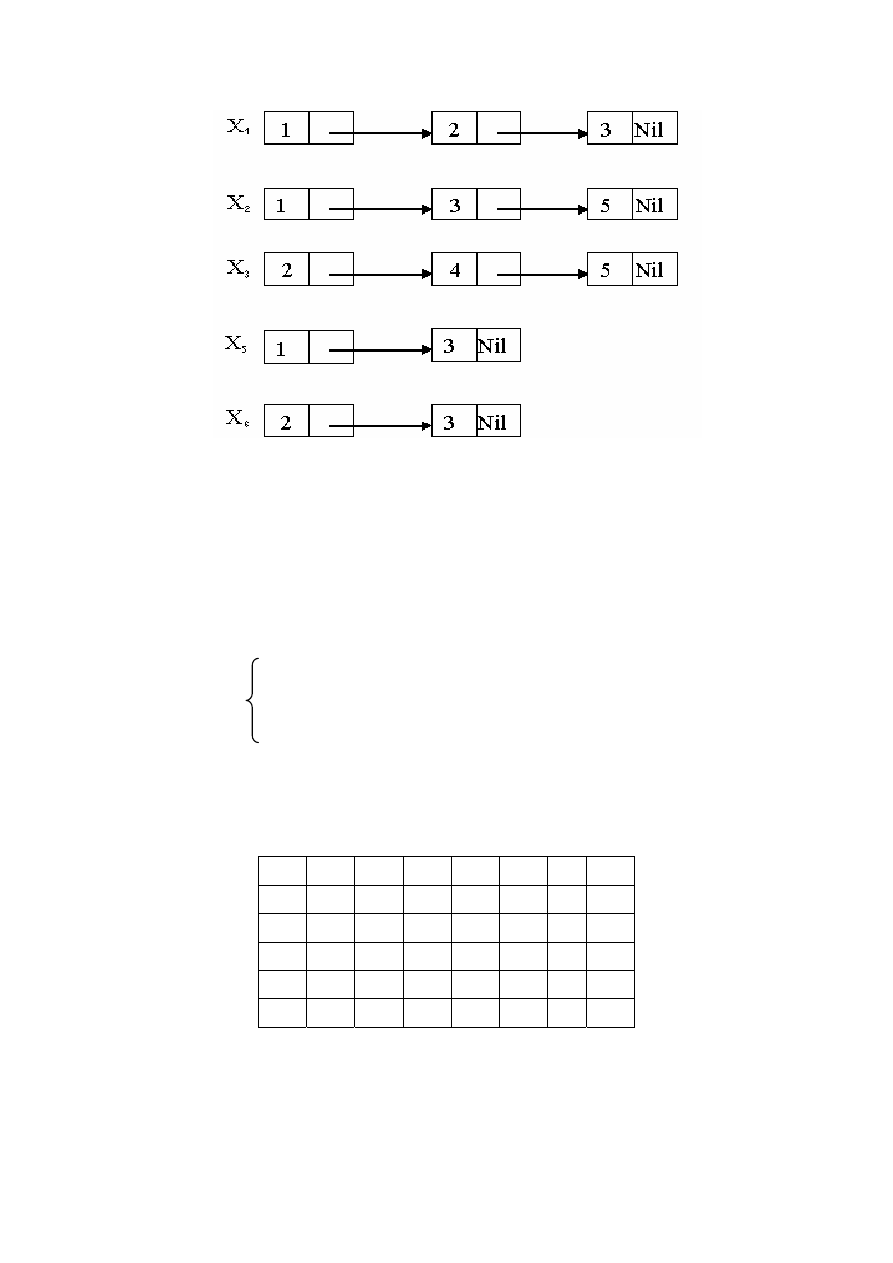
121

Рисунок 9.6 

− Задание графа списком смежности 

При

таком

представлении

каждое

ребро

в

списке

записано

дважды

. 

Прямоугольная

таблица

вида

 I = || 

i

k,ℓ

||

nym

называется

мат

-

рицей

инциденций

, 

если

ее

элементы

образуются

по

правилу

: 

1, 

если

вершина

х

k

инцидентна

ребру

 u

ℓ

; 

  i

k,ℓ    

=    

                  0, 

в

противном

случае

. 

Матрица

инциденций

I

для

графа

, 

изображенного

на

рисун

-

ке

 7.5, 

приведена

ниже

. 

u

1

u

2

u

3

u

4

u

5

u

6

  u

7

х

1

 1 1 1 0 0 0 0 

х

2

 1 0 0 1 0 1 0 

х

3

 0 0 0 0 1 1 1 

х

4

 0 0 1 0 0 0 1 

х

5

 0 0 0 1 1 0 0 

Строки

таблицы

соответствуют

вершинам

графа

, 

а

столбцы

 – 

ребрам

. 

В

каждом

столбце

не

более

двух

единиц

. 

Две

единицы

в

случае

, 

если

 u

i

ребро

, 

и

одна

 – 

если

петля

. 

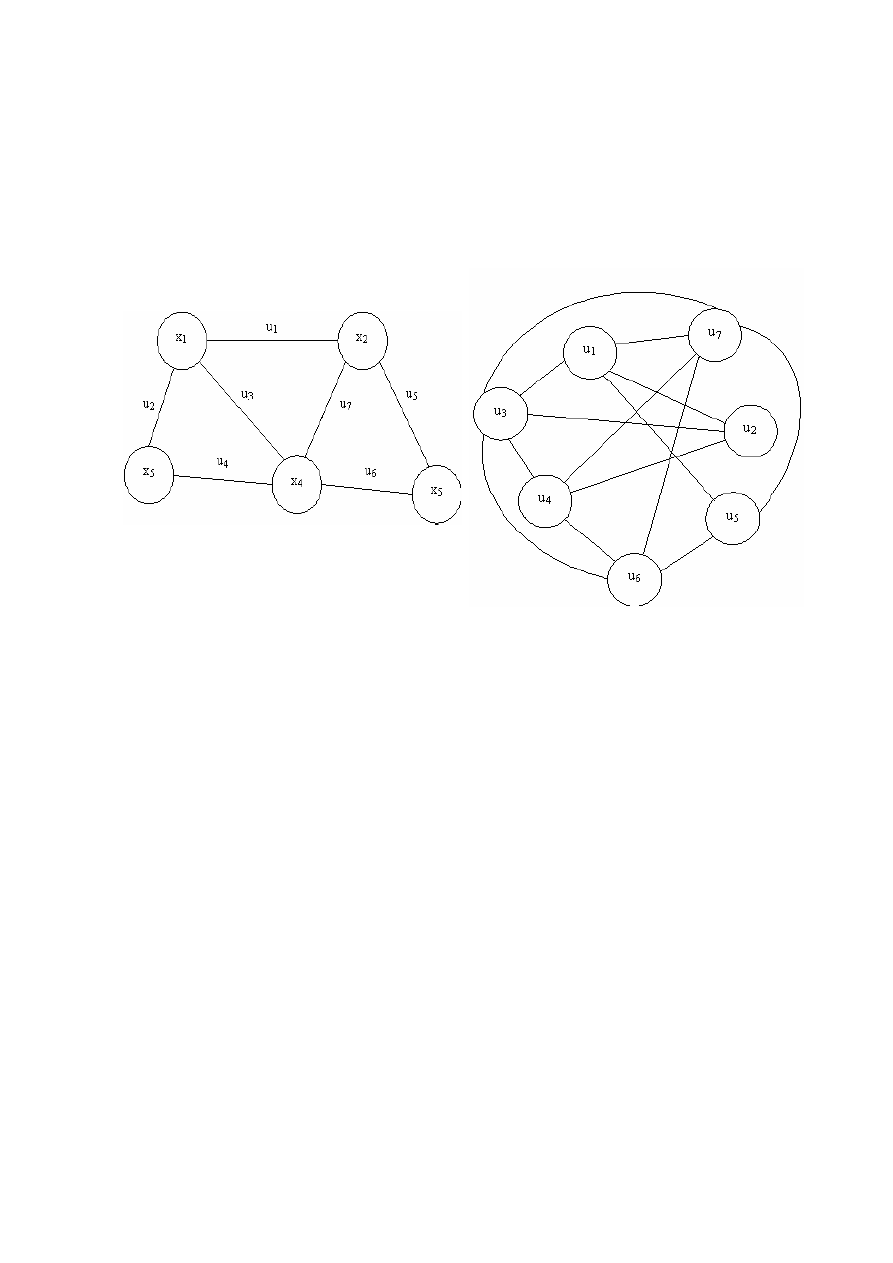
122

Матрицы

 R 

и

 I 

однозначно

задают

информацию

о

графе

. 

Можно

переходить

от

одной

матрицы

к

другой

. 

При

переходе

от

 I 

к

 R 

теряется

нумерация

ребер

. 

При

переходе

от

 R 

к

 I 

нумеруем

единичные

элементы

 r

i,j  

соответствующими

значениями

 u

k

∈U. 

Определим

граф

 G

s

 = (U, V), 

двойственный

графу

 G = (X, U). 

Рисунок 9.7  Граф G = (X, U) и двойственный ему граф G

s

 = (U, V)

Вершинами

графа

 G

s

являются

ребра

графа

 G, 

а

ребрами

 – 

па

-

ры

 (u

i

, u

j

), 

причем

ребро

 v

k

 = (u

i

, u

j

) c

оединяет

вершины

 u

i

, u

j

∈ G

s

, 

если

в

графе

 G = (X, U) 

ребра

 u

i

, u

j

∈ G

s

смежны

.  

Граф

 G 

называется

 конечным, 

если

конечны

множества

его

вершин

и

ребер

. 

Граф

, 

у

которого

множество

вершин

Х

≠ Ø 

и

множество

ре

-

бер

  U = Ø, 

называется

  нуль-графом, 

а

вершины

его

− изолиро-

ванными. 

Нуль

-

граф

обозначается

через

 G

0

. 

Граф

  G = (X, U)  | X | = n 

называется

 полным, 

если

между

любой

парой

вершин

  x

i

, x

j

∈ 

Х

имеется

ребро

 u

k

∈ U, i 

≠

 j. 

Пол

-

ный

граф

обозначается

  K

n

.  

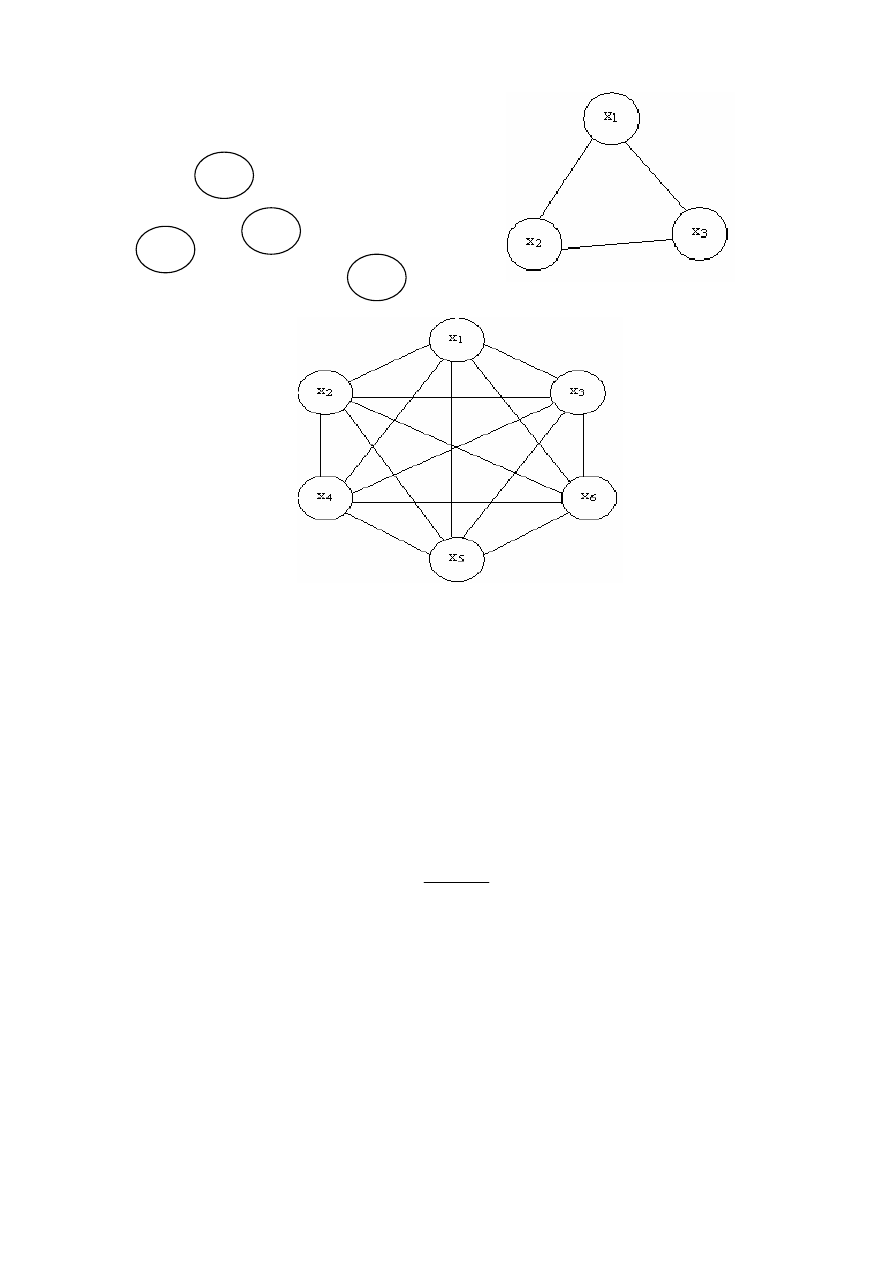
123

 
 
 
 
                              а)                       

                        б) 

в) 

Рисунок 9.8  

− Пример нуль-графа (а) и полных графов (б, в) 

Число

ребер

, 

инцидентных

вершине

  x

i

∈ 

Х

графа

, 

называет

-

ся

  локальной  степенью 

вершины

и

обозначается

ρ

(x

i

). 

Степень

изолированной

вершины

равна

нулю

. 

Вершина

называется

  вися-

чей, 

если

степень

ее

равна

единице

. 

Число

ребер

графа

 G = (X, U) 

без

петель

 | x | = n, | u | = m 

равно

Если

в

графе

имеются

петли

, 

то

каждую

из

них

нужно

счи

-

тать

дважды

. 

Вершина

называется

  четной, 

если

ее

степень

есть

четное

число

, 

и

 нечетной – 

если

ее

степень

нечетное

число

.  

Степень

любой

вершины

полного

графа

равна

 n–1, 

где

 n – 

количество

его

вершин

, 

поскольку

каждая

вершина

соединена

с

n–1 

остальными

вершинами

графа

. 

х

1

х

2

х

4

х

3

.

2

)

x

(

m

n

1

i

i

∑

−

=

ρ

124

Графы

, 

у

которых

все

вершины

имеют

одинаковую

локаль

-

ную

степень

, 

называются

  регулярными  (однородными). 

Очевид

-

но

, 

что

всякий

полный

граф

является

регулярным

. 

Число

ребер

регулярного

графа

с

локальной

степенью

 r 

равно

 m=n

·

r/2. 

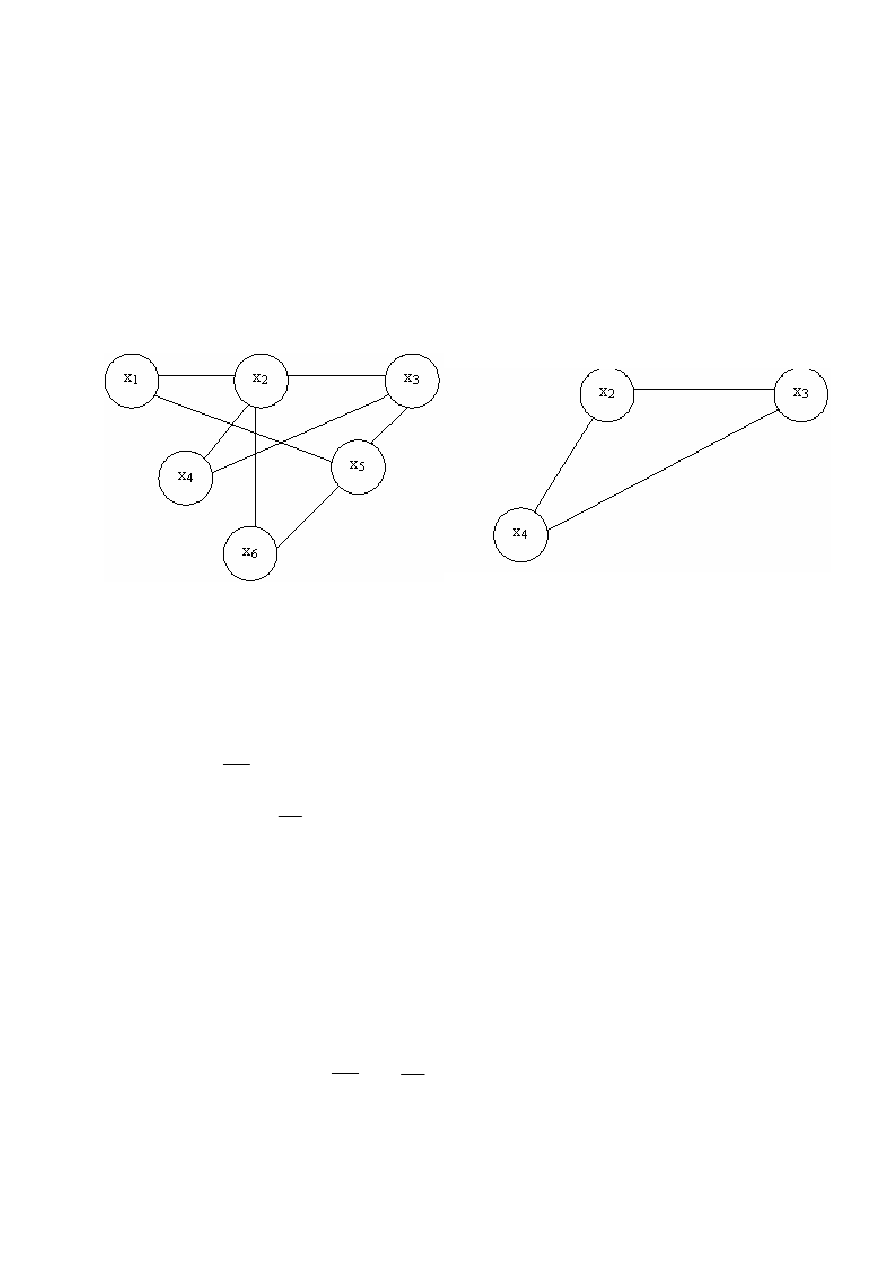
Подграфом 

графа

 G 

называется

граф

, 

у

которого

все

ребра

и

вершины

принадлежат

графу

 G, 

т

.

е

. G’’=(X’, U’)  

подграф

гра

-

фа

 G, 

если

  X’

⊆

Х

, U’

⊆U 

и

ребра

 U’ 

соединяют

только

вершины

X’. 

a) 

    б) 

Рисунок 9.9 

− Граф G=(X, U) (а) и его подграф (б) 

 
Суграфом G’=(X’, U’) 

графа

 G=(X, U) 

называют

граф

, 

у

ко

-

торого

 X’=X, U’

⊆U. 

Пример

приведен

на

ри

c

унке

 9.10. 

Граф

называется

дополнением

графа

 G 

до

полного

, 

если

множество

его

ребер

состоит

из

ребер

полного

графа

 K

n

, 

не

при

-

надлежащих

 G.      =(X, 

Ū

), 

Ū

=U

k

\U, K

n

=(X, U

k

) (

рис

. 9.10). 

Операции

над

графами

. 

Объединением

графов

 G

1

 = (X

1

, U

1

), G

2

 = (X

2

, U

2

) 

называют

граф

 G=G

1

∪G

2

=(X, U), 

где

Х

=

Х

1

∪

Х

2

и

 U=U

1

∪U

2

; 

если

Х

1

=

Х

2

и

U

1

⊂U

2

, 

то

 G=G

1

∪G

2

=G

2

; 

если

Х

1

=

Х

2

и

U

1

=U

2

, 

то

G=G

1

∪G

2

=G

1

=G

2

. 

Пример

объединения

приведен

на

рисунке

7.11. 

Пересечением

двух

графов

  G

1

и

  G

2

называется

граф

 G=(X, 

U), 

где

 X=X

1

∩X

2

и

 U=      

∩       . 

G

G

1

U

2

U

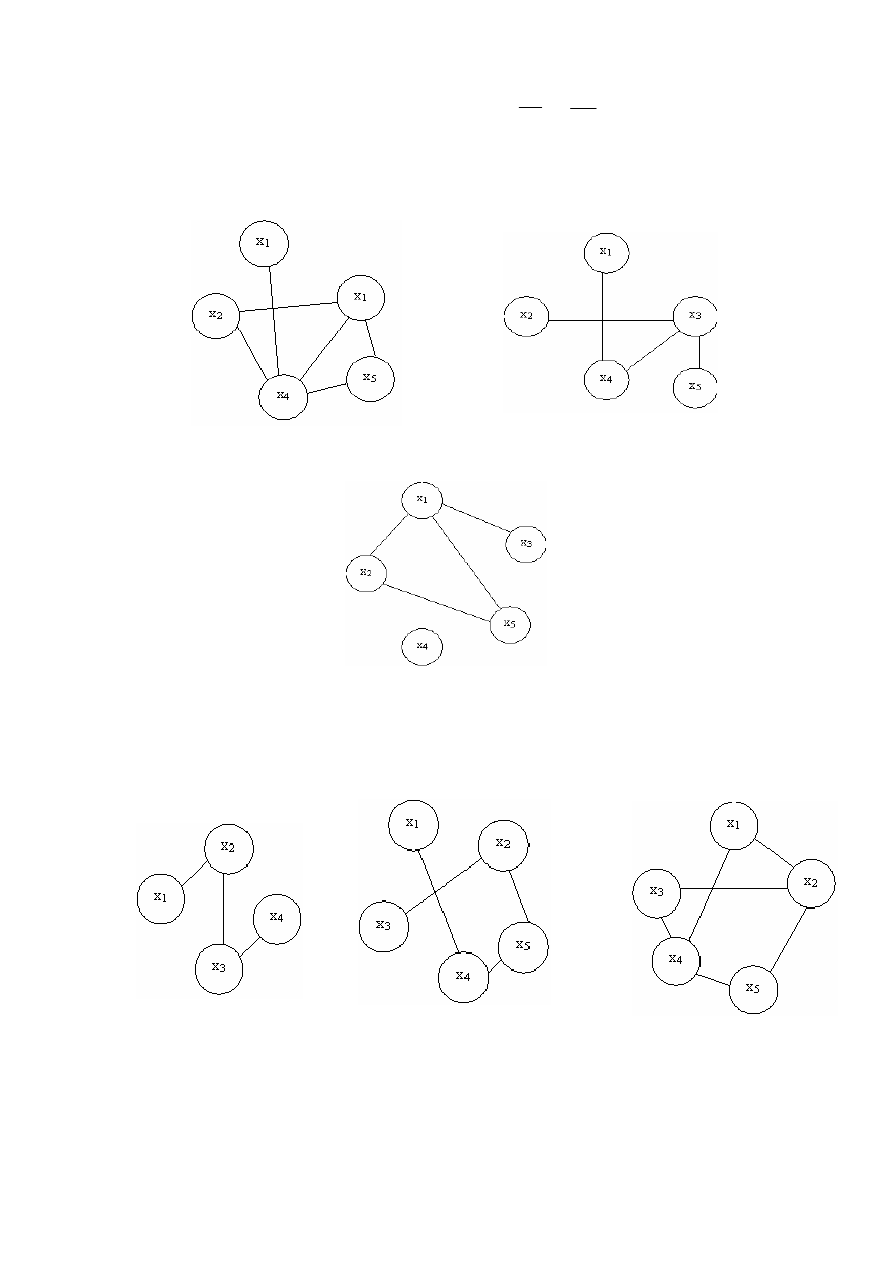
125

G=G

1

∩G

2

= 

∅, 

если

  X

1

∩X

2

 =

∅, 

а

∩       = ∅, 

то

 G=G

1

∩G

2

нуль

-

граф

. 

а)  

б) 

в) 

Рисунок 9.10  

− Граф G=(X, U) (а), его суграф (б), дополнение (в) 

Рисунок 9.11 

− Пример объединения 

U

=

1

U

2

U