Файл: Дискретная мат-ка_УП.pdf

11

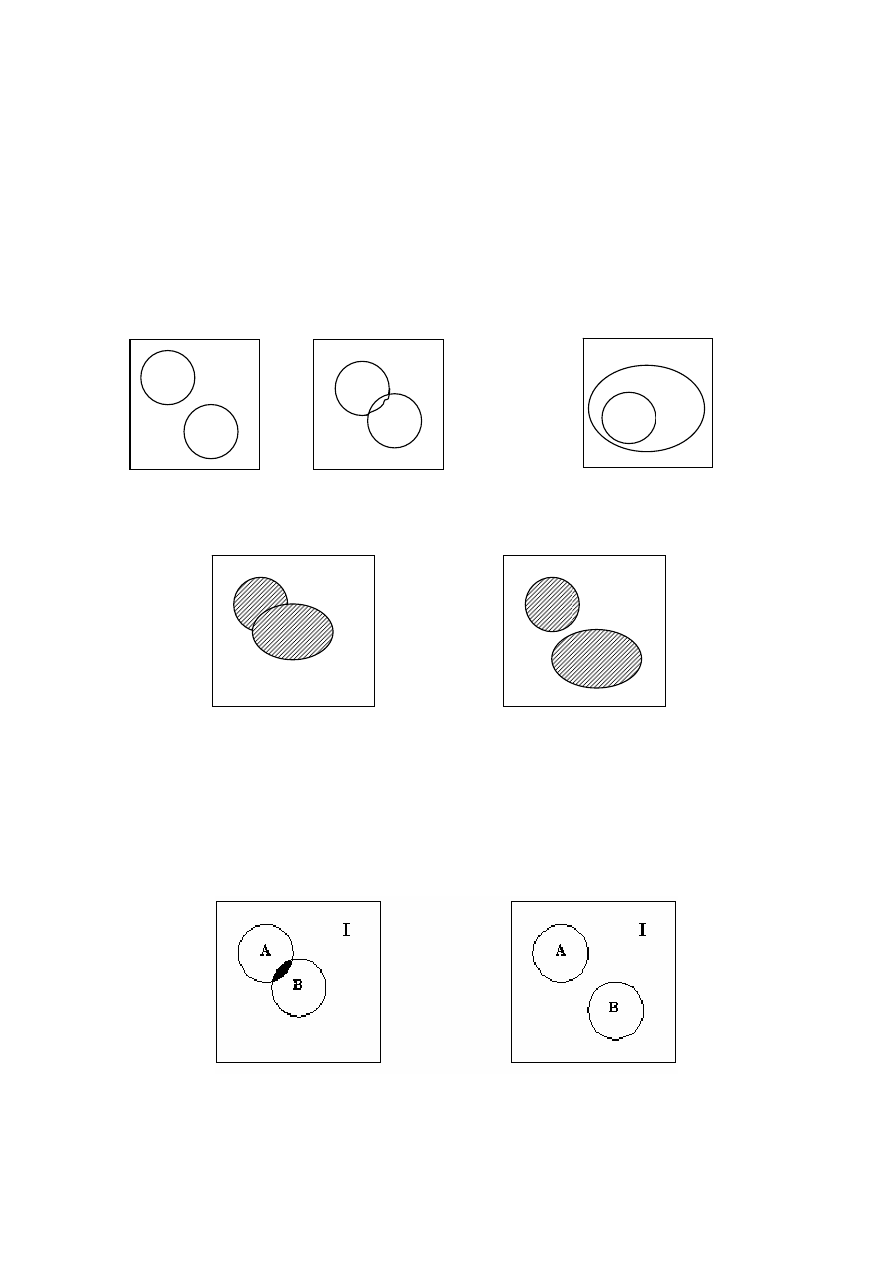
ми замкнутыми линиями. Например: на рисунке 1.1 изображены 
непересекающиеся (а) и пересекающиеся (б) множества А и В. На 
рисунке 1.2. показано отношение включения А 

⊂ В. 

Следующие  рисунки  демонстрируют  результаты  выполне-

ния операций над множествами (показаны заштрихованной обла-
стью).  Диаграммы,  приведенные  на  рисунке 1.3, демонстрируют 
объединение множеств А и В. 

 
 
 
 
 
             а)                                 б) 
         Рисунок 1.1 – Пример множеств                       Рисунок 1.2 А 

⊂ В 

Рисунок  1.3 – Объединение множеств  А 

∪В 

 
На рисунке 1.4  приведены примеры пересечения. На рисун-

ке 1.4, а приведены множества, имеющие одинаковые элементы, 
их пересечение  А ∩ В 

≠ ∅ и случай 1.4 б  множества не имеют 

общих элементов, и их пересечение А ∩ В = 

∅. 

а)                                                     б) 

Рисунок 1.4 

− Пересечение А ∩ В 

I 

A 

B 

A 

B 

I 

A 

B 

I 

I 

12

A 

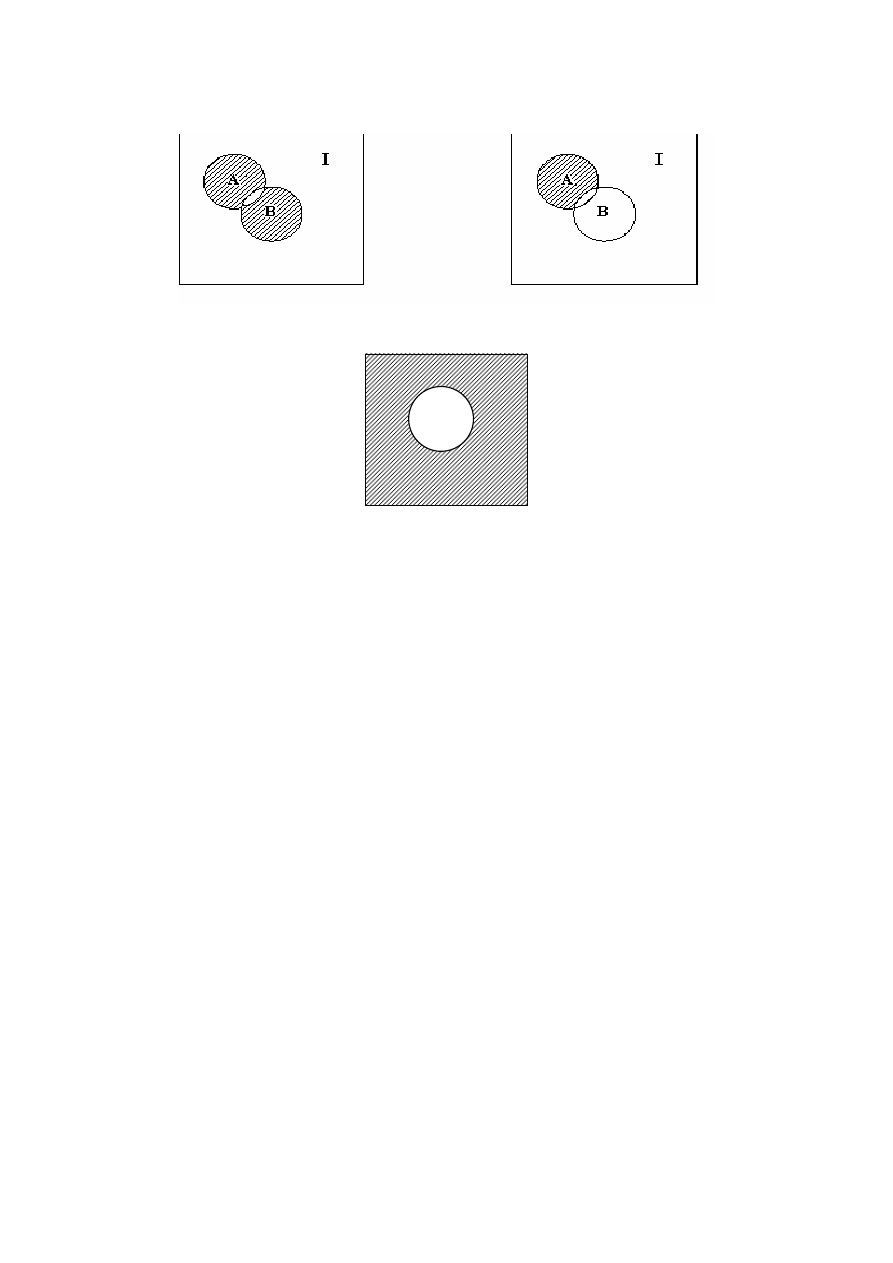
Рисунок 1.5 –  Cумма А 

⊕ В           Рисунок 1.6 –  Разность А \ В 

Рисунок 1.7 – Дополнение Ā 

1.3 

Понятие

алгебры

 
Алгеброй А называется совокупность множества М с задан-

ными в нем операциями: 

S = {f

1

, f

2

, …, f

m1

,

f

m2

, …, f

m

,

nm

 }, 

A = < M, S >, здесь множество М – носитель,  S – сигнатура ал-
гебры. Нижний индекс у идентификатора операции указывает ее 
местность. 

Алгебра вида <  M, f

2  

>  называется группоидом. 

Если f

2

 – операция типа умножения, то группоид называется 

мультипликативным, если f

2

 – операция  типа сложения, то ад-

дитивным. 

Пусть А = <M, f

2

> – группоид. Обозначим операцию f

2

  как 

•. Тогда элемент ℓ, ℓ∈ М называется правым нейтральным эле-

ментом, если m

∈ М, и m • ℓ = m. Если  ℓ • m = m – левым ней-

тральным элементом. Если выполнены оба соотношения, ℓ на-
зывается  двусторонним  нейтральным  элементом,  или  просто 
нейтральным элементом. 

Если группоид <М, •> мультипликативный, то нейтральный 

элемент называется единицей и обозначается 1. 

13

Если  группоид  <М, •> – аддитивный,  то  нейтральный  эле-

мент называется нулем и обозначается 0. 

Группоид А = <М, •> называется идемпотентным, если его 

сигнатура удовлетворяет закону идемпотентности: 

∀m ∈ M, m • m = m. 

Группоид А = <М,•>, сигнатура которого удовлетворяет за-

кону коммутативности: 

∀х,у ∈ М, х•у = у•х, 

называется коммутативным или абелевым. 

Группоид <М,•>, в котором выполняется закон ассоциатив-

ности: 

∀х,у,z ∈ М   х•(у•z)  = (x•у)•z, 

называется  ассоциативным или полугруппой. 

Полугруппа  <М,•>,  в  которой  выполнимы  обратные  опера-

ции, т.е. для любых а, b 

∈ М каждое из уравнений а•х = b, у•а = b 

обладает  единственным решением, называется группой. 

Алгебра <М, *, +>, которая по умножению является мульти-

пликативным  группоидом,  а  по    сложению – абелевой  группой, 
причем умножение связано со сложением законами дистрибутив-
ности 

а * (b+c) = a * b + a * c,  (b+c) * a = b * a + c * a, 

называется  кольцом.  Кольцо,  в  котором  все  отличные  от  нуля 
элементы составляют группу по умножению, называется телом. 
Тело, у которого мультипликативная группа абелева, называется 
полем. 

Рассмотрим алгебру множеств 
А

к

 = < B(1), 

∪, ∩, ⎯ > 

Носителем  является  булеан  универсального  множества 1, 

сигнатурой – операции 

∪, ∩, ⎯. Для операций алгебры множеств 

выполняются законы: 

1.

Коммутативности объединения и пересечения: 

А

∩В = В∩А;   А∪В = В ∪ А. 

2.

Закон ассоциативности: 

А

∪ (В∪С) = (А∪В) ∪ С; 

А 

∩(В∩С) = (А∩В) ∩С. 

3.

Закон дистрибутивности пересечения относительно объе-

динения и объединения относительно пересечения: 

14

А 

∩ (В∪С) = А∩ В∪А∩С; 

А

∪ (В∩С) = (А∪В) ∩ (А∪С). 

4.

Законы поглощения: 

А

∪А∩В = А;            А ∩ (А∪В) = А. 

5.

Законы склеивания: 

А

∩ В∪А ∩      = А;    (А∪В)  ∩ (А ∪     ) = А. 

6.

Законы Порецкого: 

А

∪Ā∩В = А∪В;   А ∩ (Ā ∪ В) = А ∩В. 

7.

Закон идемпотентности: 

А 

∪ А = А;       А ∩ А = А. 

8.

Закон действия с универсальным и пустым множествами: 

М 

∪ ∅ = М,      М ∩ ∅ = ∅,    М ∪1 = 1,  

М 

∩1 = М,    М ∪     =1,   М ∩       =∅; 

9.

Законы де Моргана 

 
 
10.

Закон двойного дополнения: 

 
 
Алгебра  множеств  является  абелевой  полугруппой,  но  не 

является группой. 

Докажем дистрибутивность А 

∪ (В ∩ С) = (А ∪ В) ∩ (А ∪ С). 

Доказательство проходит в два этапа. Обозначим левую часть как 
Z, правую – D. Требуется доказать, что если х

∈Z, то  x∈D и на-

оборот, если  x

∈D, то x∈Z. 

1.

Пусть  х

∈  А  ∪    (В  ∩  С),  это  значит,  что      х∈А    или      

х

∈(В∩С). 

Пусть   х

∈А,   тогда   х∈А ∪ В   и   х∈А ∪ С, из чего следу-

ет  х

∈(А∪ В) ∩ (А∪ С). 

Если  х

∈(В∩С), тогда х∈В  и  х∈С; из чего следует х∈А∪ В 

и х

∈А∪ С, то есть х∈(А∪ В) ∩ (А∪ С). 

Первая часть утверждения доказана. 
2.

Если х

∈(А∪ В) ∩ (А∪ С), тогда х∈А∪ В и  х∈А∪ С, 

Если х

∈А, то х∈А∪ (В∩С); 

Если х 

∉ А, то х∈  В и х∈ С, тогда х∈ В ∩ С, из чего следует 

х

∈ А ∪ (В ∩ С). 

B

B

M

M

;

B

A

B

A

,

B

A

B

A

∩

=

∪

∪

=

∩

.

A

A

=

15

1.4 

Упражнения

 
1.1. Опишите способы задания множеств. 
1.2. В чем отличие между  понятиями  принадлежности мно-

жеству и включения в множество? 

1.3.  Справедливо  ли,  что {1, 2, 3}

∈{{1, 2, 3}, {1}, {2}, {3}, 

{1, 2}}? 

1.4. Верно ли, что {1, 2, 3} 

⊂{{1, 2, 3}, 1, 2, 3, {1}}? 

1.5. Привести пример множеств А, В, С, D, таких что  A

⊂B 

и B

⊂C и C⊄D и B⊂D. 

1.6. Доказать, что (А \ В) 

∪ В = А, (А ∩ В) ∩ С = А ∩ (В ∩ С). 

1.7.  Доказать,  что  А  ∩  (В \ А) = 

∅ (Доказательство от про-

тивного). 

1.8. Укажите номера верных записей, если  А ={2, 4, 6, 8, 9}. 
а) 1

∈А; б) {2} ∈ А; в) {6, 8, 9} ∈ А; г) Ø ∈ А ? 

1.9.  Пусть  В = {a, b, {c}}. Верно  ли,  что  а

∈B, c∉B, {c}∈B, 

{a, b}

⊂B; {b}⊂B; {c}⊂ B; {{c}}⊂ B? 

1.10. Пусть C = {+, –, {+, –}}.  
Укажите верные записи: Ø 

∈C; +∈C; {+, –} ⊂ C; {{+, –}} ⊂ C; 

{+, –}

∈C. 

1.11. Заданы множества A = {1, 2, 9}, B = {2, 4, 8, 9}, C = {2, 

7, 8, 1} и универсальное множество I = {1, 2, 3, 4, 5, 6, 7, 8, 9}. 

Найти:  

.

C

B

A

)

г

;

A

B

)

в

;

B

C

)

б

;

A

B

)

a

∪

∪

∪

∪

∪

1.12.

Заданы множества А = {i, k, l}, B = {k, d, f, c}. Найти  

A 

∪ B, B ∩ A,  A \ B, B \ A, A ⊕ B, а также все подмножества А. 

1.13.

Заданы  множества A = {7, 6, 9, 4}, B = {3, 6, 7, 5, 8}.  

Найти A 

∪ B, B ∩ A, A \ B, B \ A, A ⊕ B, а также все несобствен-

ные подмножества множества А. 

1.14. Задано D = { Ø, { Ø }}. Верно ли, что { Ø }

⊂ D, Ø∈D,  

{ Ø }

∈D, Ø ⊂ D? 

1.15. Заданы множества  A = {a, b, c}, B = {b, l, f, k}, C = {a, 

c, b, k, l, m, p}. Универсальное  множество I – множество  строч-
ных букв латинского алфавита. 

Найти 

.

B

C

A

,

B

\

C

,

B

A

∪

∩

∩

1.16. 

Задано

множество

А

 = {l,  f, p}. 

Найти

его

булеан

.