ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9317
Скачиваний: 24
16
1.17.
Дано
множество
S = {a, b, c, 1, 2, 3, 4}.
Сколько
суще
-
ствует
подмножеств
этого
множества
не
содержащих
букв
?
Сколько
существует
подмножеств
,
не
содержащих
цифр
?
Сколь
-
ко
существует
подмножеств
,
не
содержащих
ни
букв
,
ни
цифр
?
1.18.
Какие
из
утверждений
верны
для
любых
А
,
В
и
С
?
а
)
если
А
∈
В
и
В
∈
С
,
то
А
∈
С
;
б
)
если
А
∩
В
⊆
С
и
А
∪
В
⊆
С
,
то
А
∩
С
=
∅;
в
)
если
А
≠
В
и
В
≠
С
,
то
А
≠
С
;
г
)
если
∅
=
∪
⊆
∪
⊆
B
то
,
C
A
B
и
C
B
A
1.19.
Нарисовать
диаграммы
Эйлера
-
Венна
:
а
) (
А
∪
В
)
∩ (
В
∪
С
)
∪ (
В
∩
Ā
),
б
)
А
∩ (
В
∪ I) ∩ (
С
∩ I )∩ (A∪C),
в
) (A
∪ B) ∩ (
C
∩ B) ∩ (A ∩ B) ∪ (C ∩
Ā
).
1.20.
Нарисовать
диаграммы
Эйлера
-
Венна
:
а
) (A
∪ B) ∩
)
C
A
(
∩
∩ (A ∪ B ),
б
) I
∩ (A ∪ C) ∩
)
C
B
(
∩
∪ (A ∩ (B ∪ C)),
в
) (A
∩ B) ∪
)
C
A
(
∩
∪ (B ∩ C).
1.21.
Нарисовать
диаграммы
Эйлера
-
Венна
:
а
) (A
⊕ B) ∩ (A ⊕ C),
б
) A
⊕
Ā
∩
B
⊕
Ā
∩ B,
с
) A
⊕ B ⊕ A ∩ B.
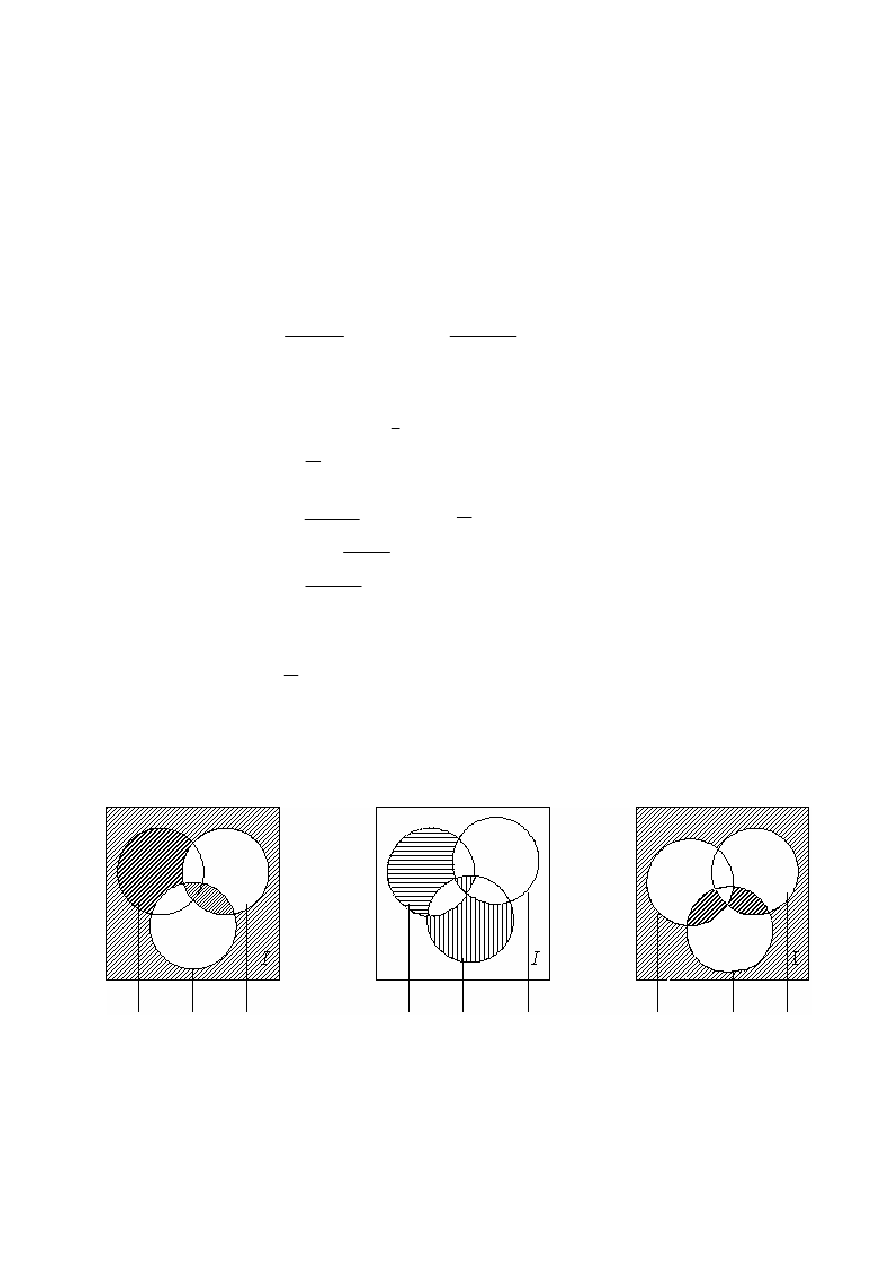
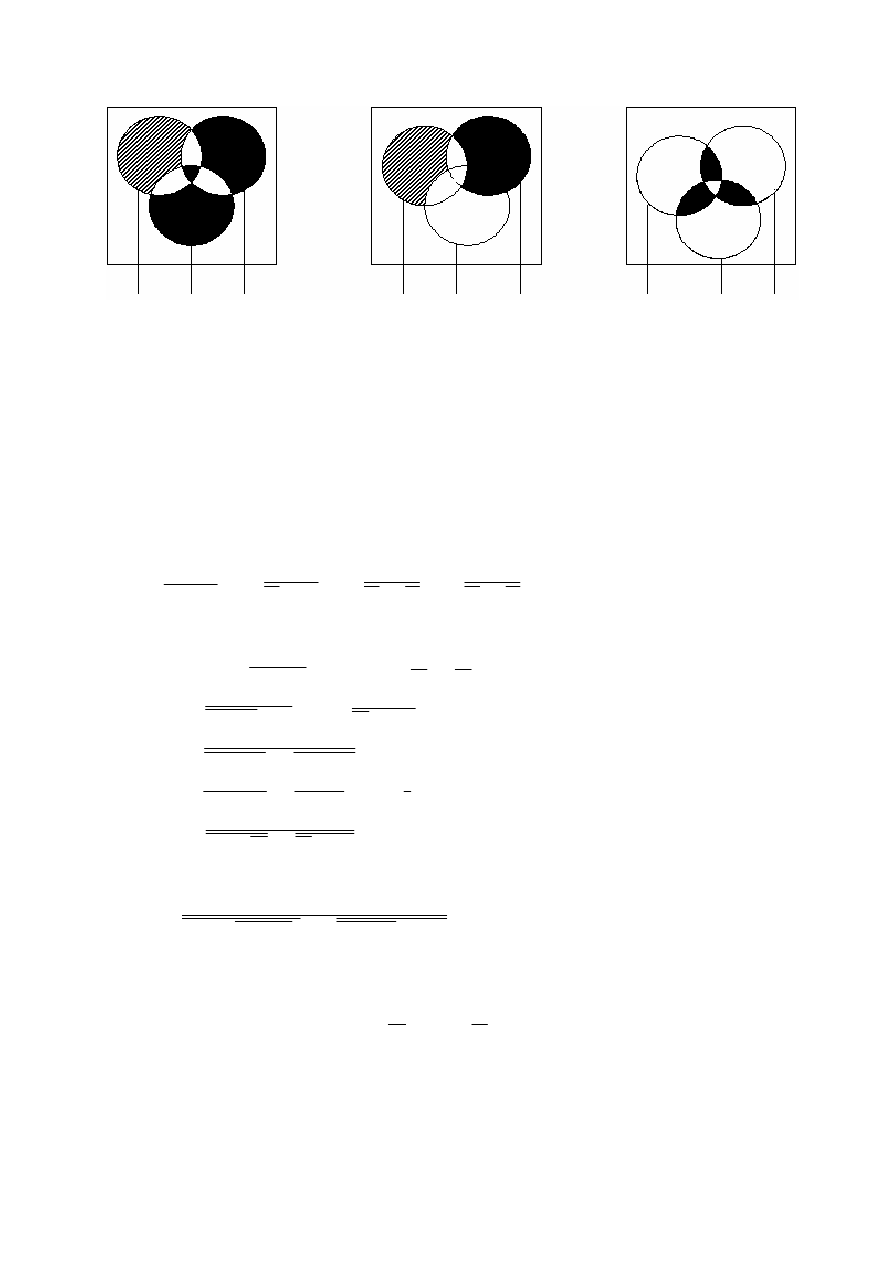
1.22.
Записать
формулу
по
диаграммам
Эйлера
-
Венна
.
A C B A C B A C B
Рис.
1.8
Рис. 1.9
Рис. 1.10
17
A C B A C B A C B
Рис. 1.11
Рис. 1.12
Рис. 1.13
1.23.
Доказать
,
что
А
∩ (
В
\
А
) =
∅.
1.24.
Укажите
пустые
множества
:
а
)
А
∪ ∅;
∅ ∪ ∅ ∩
А
;
б
)
А
∩
В
∩ ∅;
I
∪ ∅ ∩ A;
с
) (A
∪ B) ∩ I∩ ∅; I ∩ ∅ ∪ ∅.
1.25.
Упростить
выражения
,
если
В
⊃
А
.
1.26.
Равны
ли
следующие
выражения
:
1. 27.
Упростить
выражения
:
б
) (
С
∩ (
А
∪
В
∪
С
)) \
В
;
в
)
А
⊕
А
⊕
А
⊕
А
;
1.28.
Указать
верные
выражения
:
а
)
А
∩ (
В
⊕
С
) =
А
∩
В
⊕
А
∩
С
;
б
)
А
⊕
В
⊕
А
∩
В
=
А
∪
В
;
.
B
A
)
г
;
B
A
)
в
;
B
A
)
б
;
B
A
)
a
∩
∪
∪
∪
.
I
и
B
B
A
A
)
д
;
I
и
I
B
A
)
г
;
A
и
A
A
A
A
)
в
;
A
и
I
I
A
)
б
;
С
В
А
и
C
B
A
)
a
∩
∩
∩
∩
∪
∅
∩
∪
∪
∪
∅
∪
∪
∪
∪
∪
∩
∪
;
C
)
B
A
(
)
C
B
(
A
)
а
∩
∪
∪
∪
∩
.
D
C
B
A
D
С
А
С
В
А
)
г
∩
∩
∩
∪
∩
∩
∪
∩
∩
18
в) (A
⊕ I) ∩ A = ∅;
г) (A
⊕ I ⊕ I) ∩A = ∅.
1.29. Упростить выражения:
1.30. Найти элементы множеств, если
А = {1, 2, 4, 5}; B = {1, 3, 6, 7}; C = {3, 2, 6, 7}.
а) A
∩ B ∩ C ∪ B ∩ C ∪ B ∩
C
;
б) (A
⊕ В) ∩ С;
1.31. Упростить выражения, если B = I, A =
∅ :
(А
∪В) ∩ (С∪D);
(A
∩C) ∪ ( B ∩C) ∪ (A∩B);
A
∩ D ∩C∪B∩C∩D;
A
∩ (B∪C∪D) ∩B∩C;
A
∩ (∪B∪C) ∩ (C ∪ D ∪ B);
(A
∪ B ∪ C) ∩ (
B
∪D).
1.32. Доказать, что два множества равны тогда и только то-
гда, когда результаты их объединения и пересечения совпадают.
1.33. Известно, что из 100 студентов живописью увлекаются
28, спортом
− 42, музыкой − 30, живописью и спортом − 10, жи-
вописью и музыкой
− 8, спортом и музыкой − 5, живописью,
спортом и музыкой
− 3.
Определить количество студентов:
а) увлекающихся только спортом;
б) ничем не увлекающихся.
.
D
C
B
A
C
A
D
C
A
C
B
A
)
ж
);
C
B
(
B
)
B
A
(
)
е
);
D
B
A
(
)
B
A
(
)
д
);
B
B
B
A
(
B
)
г
;
D
C
A
C
B
A
C
A
)
в
;
C
D
C
B
A
)
б
;
B
A
C
B
A
)
а
∩
∩
∩
∪
∩
∪
∩
∩
∪
∩
∩
∪
∩
∩
∪
∪
∪
∩
∪
∩
∪
∩
∩
∩
∩
∪
∩
∩
∪
∩
∪
∩
∩
∩
∩
∪
∩
∩
.
B
)
C
B
A
(
)
C
B
A
(
)
д
);
C
B
A
(
)
C
B
(
)
B
A
(
)
г
);
C
B
A
(
)
C
B
A
(
)
в
∩
∪
∪
∩
∪
∪
∩
∩
∩
∩
∩
∪
∪
∩
∩
∪
∩

19
1.34. Экзамен по математике сдавали 250 абитуриентов,
оценку ниже пяти баллов получили 180 человек, а выдержали
этот экзамен 210 абитуриентов. Сколько человек получили оцен-
ки 3 и 4?
1.35. В школе 1400 учеников. Из них 1250 умеют кататься на
лыжах,952 – на коньках. Ни на лыжах, ни на коньках не умеют
кататься 60 учащихся. Сколько учащихся умеют кататься и на
лыжах, и на коньках?
1.36. В группе из 100 туристов 70 человек знают английский
язык, 45 знают французский язык и 23 человека знают оба языка.
Сколько туристов в группе не знают ни английского, ни француз-
ского языка?
1.37. В олимпиаде по математике принимало участие 40
учащихся. Им было предложено решить одну задачу по матема-
тике, одну по геометрии и одну по тригонометрии. Результаты
проверки:
Решены задачи
Кол-во решивших
По алгебре 20
По тригонометрии 18
По геометрии 18
По алгебре и геометрии 7
По алгебре и тригонометрии 8
По геометрии и тригонометрии 9
Известно также, что ни одной задачи не решили трое.
Сколько учащихся решили все три задачи? Сколько учащихся
решили две задачи?
1.38. Пусть А – подмножество множества натуральных чи-
сел, каждый элемент множества А есть число, кратное или 2, или
3, или 5. Найти число элементов в множестве А, если среди них
имеется: 70 чисел, кратных 2; 60 чисел, кратных 3; 80 чисел,
кратных 5; 32 числа, кратных 6; 35 чисел, кратных 10; 38 чисел,
кратных 15, и 20 чисел, кратных 30.
1.39. В штучном отделе магазина посетители обычно поку-
пают либо один торт, либо одну коробку конфет, либо один торт
и одну коробку конфет. В один из дней было продано 57 тортов и

20
36 коробок конфет. Сколько было покупателей, если 12 человек
купили и торт и коробку конфет?
1.40. В спортивном лагере 65% ребят умеют играть в фут-
бол, 70% – в волейбол и 75% – в баскетбол. Каково наименьшее
число ребят, умеющих играть и в футбол, и в волейбол, и в бас-
кетбол?
1.41. Каждый из учеников класса в зимние каникулы ровно
два раза был в театре, при этом спектакли А, В и С видели соот-
ветственно 25, 12 и 23 ученика. Сколько учеников в классе?
Сколько из них видели спектакли А и В, А и С, В и С?
1.42. В течение недели в кинотеатре демонстрировались
фильмы А, В и С. Из 40 школьников, каждый из которых про-
смотрел либо все три фильма, либо один из трех, фильм А видели
13, фильм В – 16, фильм С – 19 школьников. Сколько учеников
просмотрели все три фильма.
1.43. В отряде из 40 ребят 30 умеют плавать, 27 умеют иг-
рать в шахматы и только пятеро не умеют ни того ни другого.
Сколько ребят умеют плавать и играть в шахматы?
1.44. На уроке литературы учитель решил узнать, кто из 40
учеников класса читал книги А, В и С. Результаты опроса оказа-
лись таковы: книгу А читали 25 учащихся, книгу В – 22, книгу С
– также 22. Книги А или В читали 33 ученика, А или С – 32, В
или С – 31; все три книги прочли 10 учащихся. Сколько учени-
ков прочли только по одной книге? Сколько учащихся не читали
ни одной из этих трех книг?
1.45. Среди абитуриентов, выдержавших приемные экзаме-
ны в вуз, оценку «отлично» получили: по математике – 48 абиту-
риентов, по физике – 37, по русскому языку – 42, по математике
или физике – 75, по математике или русскому языку – 76, по фи-
зике или русскому языку – 66, по всем трем предметам – 4.
Сколько абитуриентов получили хотя бы одну пятерку? Сколько
среди них получивших только одну пятерку?