ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9320
Скачиваний: 24
21
2
ОТНОШЕНИЯ
Понятие отношения используют для обозначения связи ме-
жду объектами или понятиями.
Декартовым произведением
множеств
А х В
называют
третье множество
С,
элементами которого служат пары всех
элементов множеств
А
и
В
, при этом первый элемент берется из
множества
А
, второй – из множества
В
.
Пример:
А = {a
1
, a
2
, a
3
}; B = {b
1
, b
2
, b
3
}.
A x B = {<a
1
, b
1
>, <a
2
, b
1
>, <a
3
, b
1
>, <a
2
, b
1
>, <a
2
, b
2
>, <a
2
, b
3
>,
<a
3
, b
1
>, <a
3
, b
2
>, <a
3
, b
3
>}.
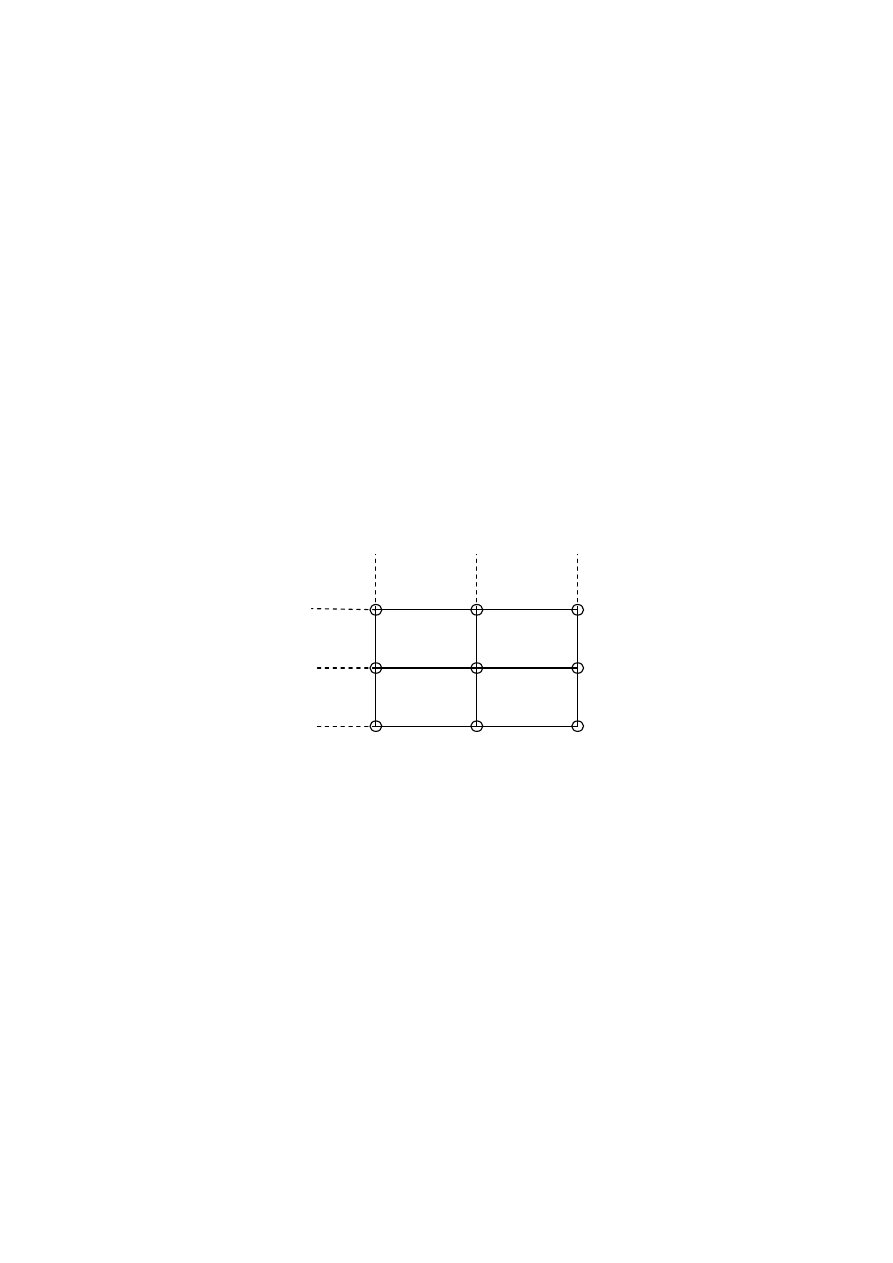
Сопоставим с декартовым произведением двух множеств
прямоугольную решетку, узлы которой взаимно однозначно со-
ответствуют элементам декартова произведения.
Рисунок 2.1
− Решетка декартова произведения
Декартовым произведением n множеств
А
1
, А
2
,…, А
n
на-
зывают множество
С= А
1
х А
2
х…х А
n
.
Каждый элемент
С
рассматривается как упорядоченное
множество
с
i
=<a
i
1
, a
i
2
,…,a
i
n
>,
называемое
кортежем
.
Кортеж состоит из компонент, для которых задается место-
положение. Кортеж может иметь одинаковые компоненты. Число
компонент кортежа называют его
длиной
. Два кортежа считаются
равными,
если их длина одинакова и соответствующие компо-
ненты равны между собой. Компонентами кортежа могут быть
любые объекты, в том числе множества и кортежи.
b
1
b
2
b
3
a
1
a
2
a
3
22
Примеры.
1.
Пусть Y = {1, 2, 3}, X = {3, 4};
Y x X = {<1, 3>, <1,4>, <2,3>, <2,4>, <3,3>, <3,4>};
X x Y = {<3,1>, <3,2>, <3,3>, <4,1>, <4,2>, <4,3>}.
Необходимо отметить, что Y x X ≠ X x Y.
2.
Пусть заданы кортежи:
α = <1,2,3,2>, β = <1,3,2,2>, γ = <1,2,3,2>, δ = <2,1,3,2>.
Здесь α ≠ β, α = γ, α ≠
δ.
Степенью
S
множества
A
называется его прямое произведе-
ние самого на себя S раз.
Любое подмножество
R
⊆
X x Y
декартова произведения
множеств называется
бинарным отношением
из
X
в
Y.
Если
R
есть некоторое отношение, и пара
<x,y
> принадле-
жит этому отношению, то наряду с записью
<x,y>
∈
R
, употреб-
ляется запись
xRy.
Областью определения
бинарного отношения R называет-
ся множество
A
R
={x| существует такое y, что xRy}.
Областью значений
бинарного отношения
R
называется
множество
B
R
= {y| существует такое x, что xRy}.
Пример.
Пусть даны множества: A = {1,2,3,4,5,6,7}, B = {1,2,3}. По-
строим отношение R
⊂АxB, y∈B есть делитель x∈A(xRy).
R = {<1,1>, <2,1>, <3,1>, <4,1>, <5,1>, <6,1>, <7,1>, <2,2>,
<4,2>, <6,2>, <3,3>, <6,3>}.
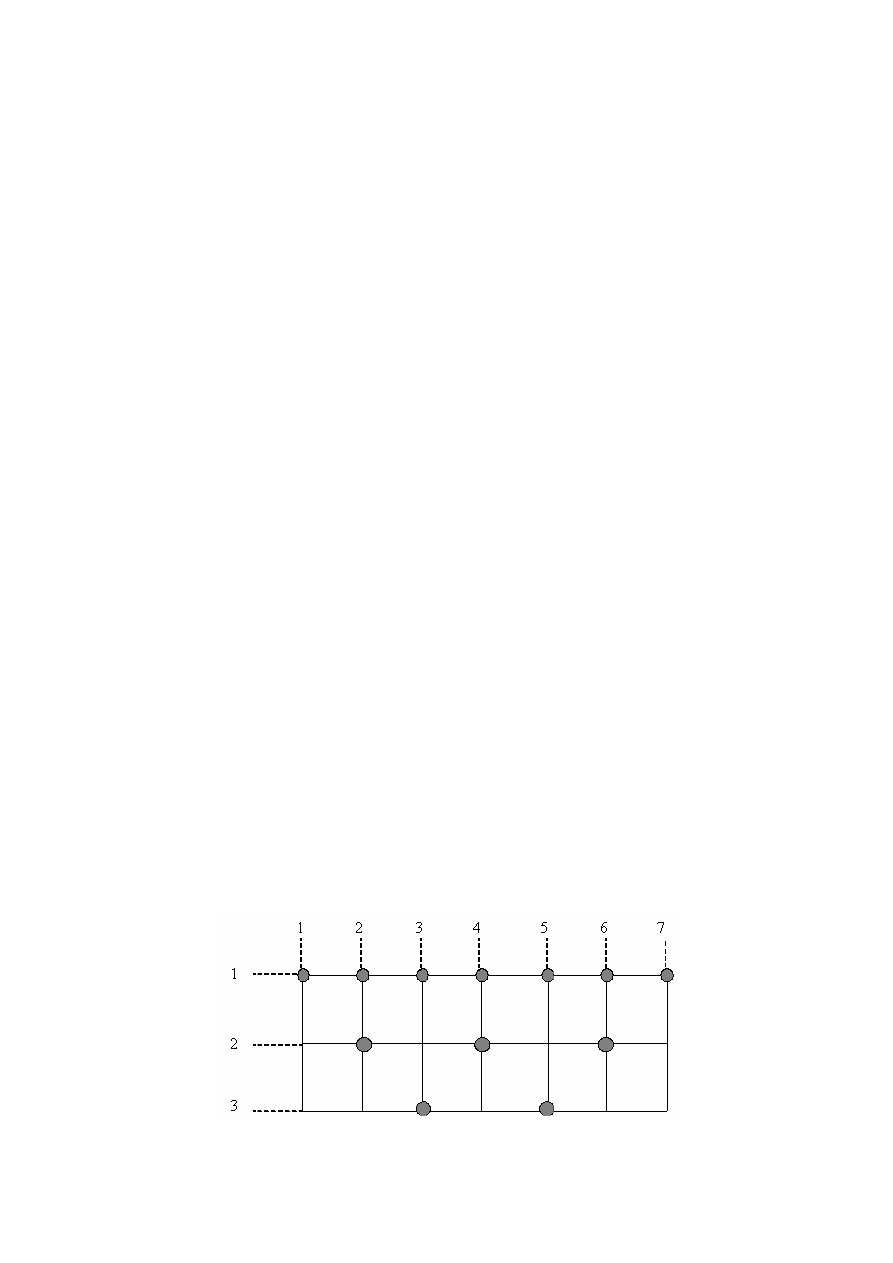
Используя решетку, отношение можно изобразить следую-
щим образом.
Рисунок 2.2 – Отношение «есть делитель»
s
s
A
...
A
A
A
×
×
×
=
23
Подмножество R обозначено зачернением соответствующих
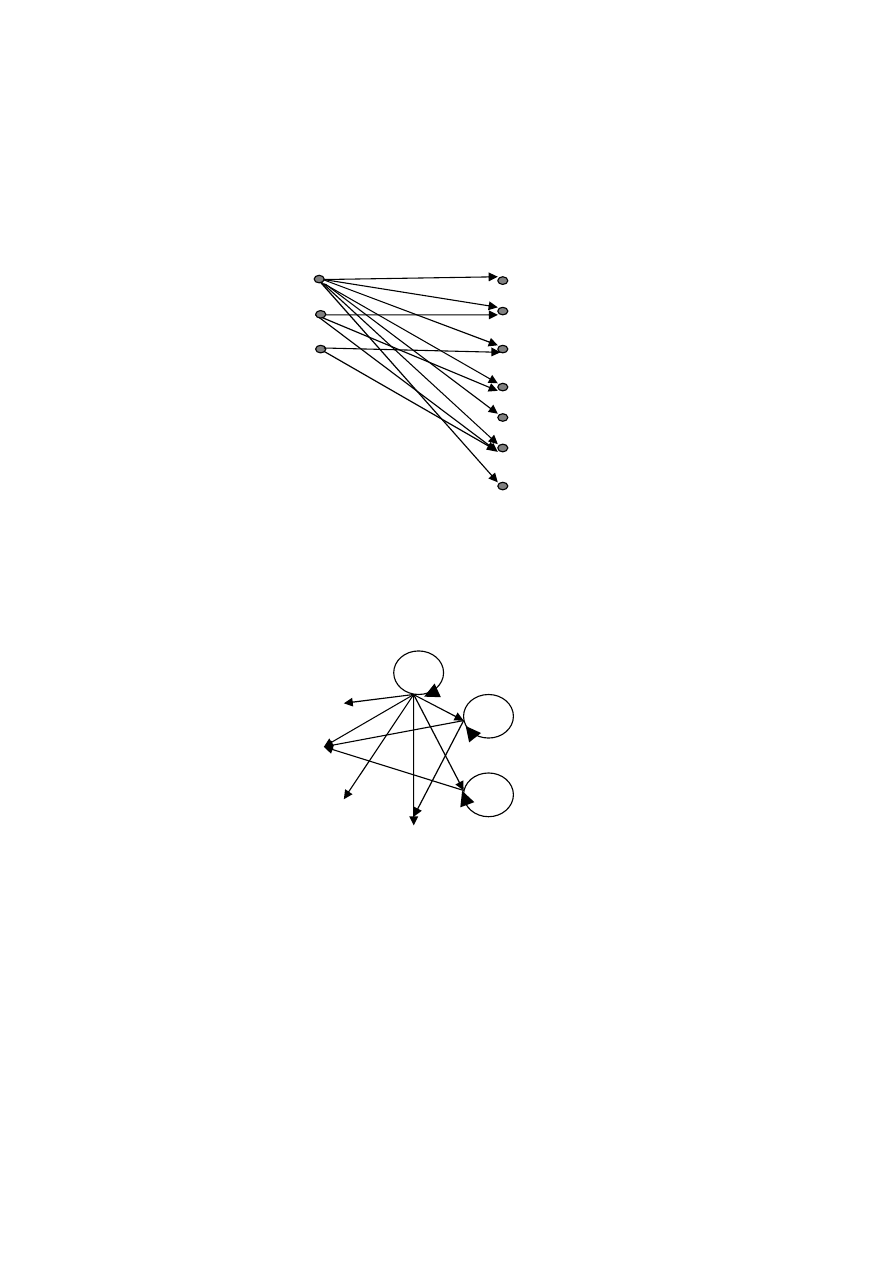
узлов решетки. Графическое представление данного отношения
или представление графом (отношения представлены стрелками)
показано на рисунке 2.3.
В
А
1
1
2
2
3
3
4
5
6
7
Рисунок 2.3
− Графическое изображение отношения
Так как элементы множества В
⊂ А, то можно показать от-
ношение R способом, представленным на рисунке 2.4.
Рисунок 2.4
− Графическое изображение отношения
Квадратом множества
Х
называется декартово произве-
дение двух равных между собой множеств:
Х х Х = Х
2
.
Бинар-
ным отношением Т
в множестве
Х
называется подмножество
его квадрата
Т
⊂
Х
2
. Совокупность множества
Х
с заданным в
нем бинарным отношением
Т
⊂
Х
2
называется
графом G.
G = (X, T),
где
Х
– множество вершин (носитель графа);
Т
– множество дуг (сигнатура графа).
1
2
3
7
6
5
4

24
Пусть задано декартово произведение А х В. И пусть с
∈ А х В,
с = <x, y>, x
∈A, y∈B.
Проекцией
элемента
с
на множество
А
назовем элемент
х.
Сечением R
⊂
A x B
по элементу
х
∈А
называется множест-
во элементов
у
∈В
таких, что
<x,y>
∈ R, R ⊂ А x B.
Вместо термина сечение часто употребляется термин
окре-
стность единичного радиуса
.
Множество всех сечений, взятых для всех элементов множе-
ства
А
при задании на нем отношения
R
⊂
А x B
, называется
фактормножеством
.
Фактормножество полностью определяет отношение R.
Рассмотрим предыдущий пример. Пусть Х
⊂ А, и Х = {2,7}.
Тогда сечение R(X) = R(2)
∪ R(7) = {1,2} ∪ {7} = {1,2}. Фак-
тормножество определяется как множество всех сечений R по
всем элементам из А. Зададим фактормножество в виде двух
строк, в первой из которых поместим элементы множества А, а во
второй под каждым элементом запишем сечение по этому эле-
менту.
⎥
⎦
⎤
⎢
⎣
⎡
}
1
{
}
3
,
2
,
1
{
}
1
{
}
2
,
1
{
}
3
,
1
{
}
2
,
1
{
}
1
{
7
6
5
4
3
2
1
Вторая строка задает фактормножество. Сечение и фак-
тормножество наглядно представлены решеткой на рисунке 2.2.
2.1
Операции
над
отношениями
Для бинарных отношений обычным образом определены тео-
ретико-множественные операции объединения, пересечения и др.
Пусть R
1
⊂ А х С отношение из А в С, а R
2
⊂ С х В – отно-
шение из С в В.
Композицией
двух отношений
R
1
и
R
2
называется отно-
шение
R
⊂
А х В
из
А
в
В
, определяемое следующим образом:
R = R
1
○R
2
= {<a,b>| cуществует С такое, что <a,c>
∈
R
1
и
<c,b>
∈
R
2
}
Обратным
отношением для
R
называется отношение
R
1
= {<a,b>| <b,a>
∈
R}.
25
Для любых бинарных отношений выполняются свойства:
Свойство
1:
(R
–1
)
–1
= R
Cвойство
2: Пусть S, R – отношения, тогда
(S, R)
–1
= R
–1
○ S
–1
Свойство
3: Если R
⊂ S и T ⊂ Y, то
T R
⊂ Y S
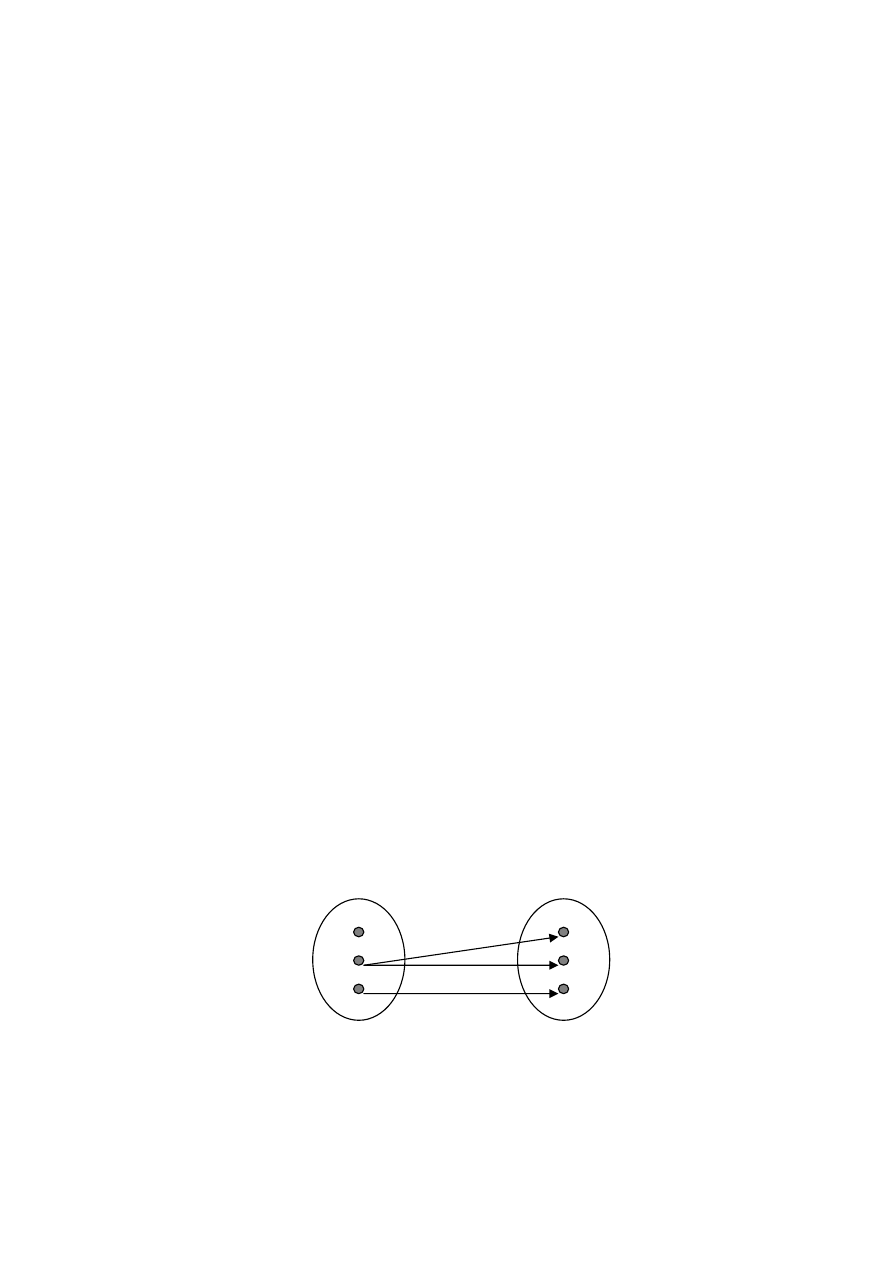
Функция f : A→B
может быть определена как отношение,
определенное на множестве
А х В
, обладающее свойством:
Если
(a,b)
∈
f
и
(a,c)
∈
f
, то
b = c.
Область определения
функции обозначается как
D
f
, а
об-
ласть ее значений
как
R
f
.
Если D
f
=А и R
f
⊆В, то говорят, что функция f задана на
множестве А со значениями во множестве В и осуществляет ото-
бражение множества А во множество В. Вместо <a,b>
∈ f, пишут b
= f(a), здесь b – значение функции, соответствующее аргументу а.
Пусть
f : A→B
. Функция называется
инъективной
, если для
любых
а
1
, а
2
, b
из
b=f(a
1
)
и
b=f(a
2
) следует, что
a
1
=a
2
(рисунок
2.6).
Функция
f
называется
сюръективной
, если для любого
элемента
b
∈
B
существует элемент
а
∈
А
такой, что
b=f(а
) (рису-
нок 2.7).
Функция f называется
биективной
, если
f
одновременно
сюръективна и инъективна (рисунок 2.8).
Если существует биективная функция
f : А →В
, то говорят,
что f осуществляет взаимнооднозначное соответствие между
множествами
А
и
В
.
Рисунок 2.5 – Отношение, но не функция
А
В