ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 9321
Скачиваний: 24
26
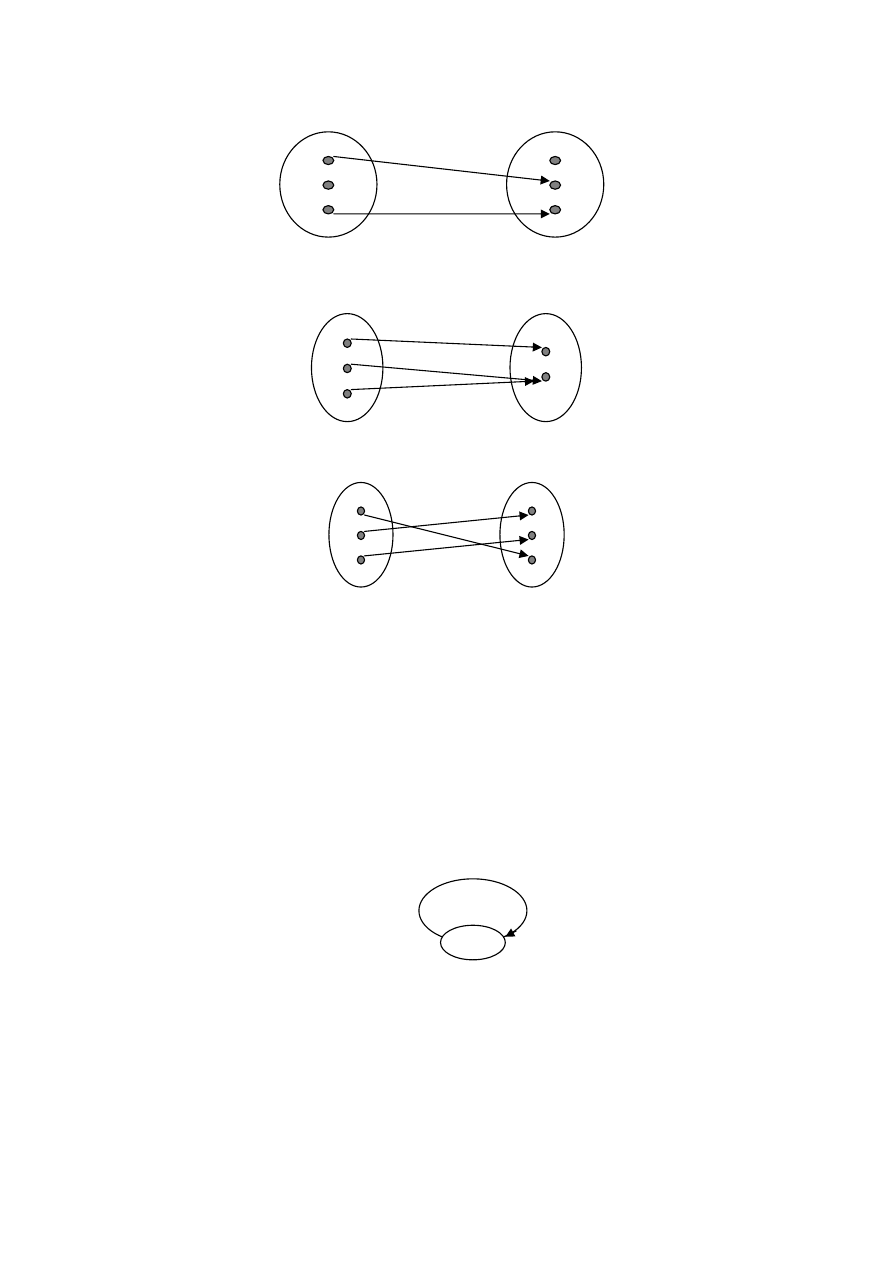
Рисунок 2.6 – Инъективная функция
Рисунок 2.7 – Сюръективная функция
Рисунок 2.8 – Биективная функция
2.2
Свойства
бинарных
отношений
Рассмотрим наиболее важные свойства бинарных отноше-
ний. Пусть задано множество А, А х А=А
2
и отношение R на нем.
Отношение R в множестве А называется
рефлексивным
, ес-
ли для каждого элемента
а
∈
А
справедливо утверждение
a R a.
Если изображать рефлексивность графически, то элемент имеет
петлю.
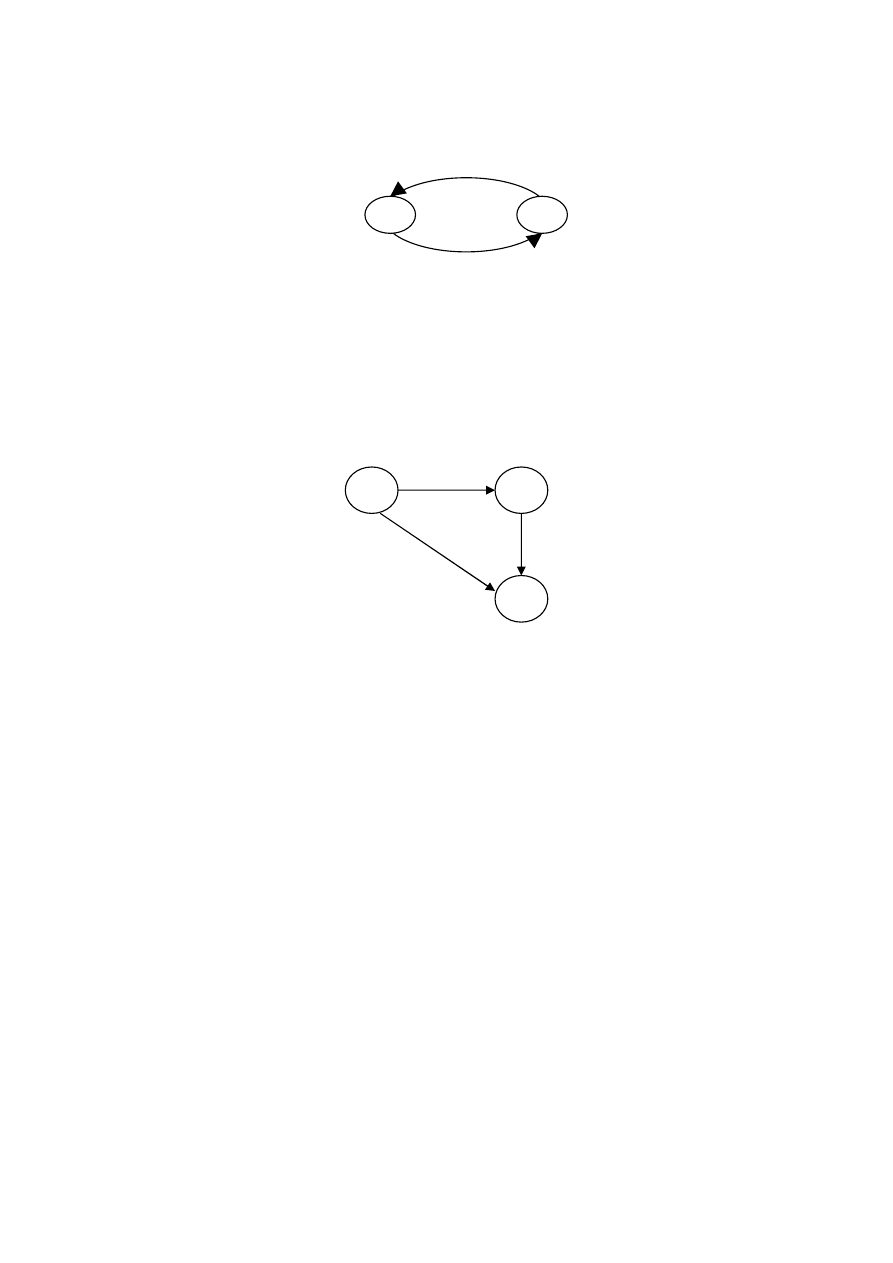
Рисунок 2.9 – Рефлексивное отношение
Отношение
R
в множестве
А
называется
симметричным
,
если для любых
а,b
∈
A
выполнено:
aRb
следует
bRa
; или
(a,b)
∈
R
⇒ (b,a)
∈
R a
≠
b.
А
В
А
В
А
В
а
27
Графически симметричность можно изобразить следующим
образом:
Рисунок 2.10 – Симметричное отношение
Отношение
R
называется
транзитивным
, если для любых
a,b,c
∈
А
, выполняется:
a R b
и
b R c
⇒ a R c
, при этом
a
≠
b, b
≠
c,
a
≠
с
. Граф, представляющий транзитивное отношение R, выгля-
дит следующим образом:
Рисунок 2.11 – Транзитивное отношение
При этом дуга
(а,с)
называется
транзитивно замыкающей
дугой.
Бинарное отношение
R
в множестве
А
, обладающее свойст-
вами:
рефлексивности: для каждого
a
∈
A, (a,а)
∈
R
;
транзитивности: для любых
a,b,с
∈
A
следует
(a,b)
∈
R,
(b,с)
∈
R
⇒ (a,с)
∈
R,
называется отношением
упорядоченности
и обозначается
≤
.
Если любые два элемента
а, b
упорядоченного множества
находятся в отношении упорядоченности
a
≤
b
или
b
≤
a
, то это
множество называется
линейноупорядоченным
, в противном
случае –
частично упорядоченным
.
Например, отношение a
≤ b на множестве действительных
чисел является отношением упорядоченности. Во множестве
подмножеств некоторого универсального множества U отноше-
ние А
⊆В также есть отношение упорядоченности. Схема органи-
а
b
c
а
b
28
зации подчинения в учреждении есть отношение частичного по-
рядка на множестве должностей.
Бинарное отношение в множестве А, обладающее свойства-
ми антирефлексивности, антисимметричности и транзитивности,
называется
отношением строгой упорядоченности
и обознача-
ется
<
.
Рассмотрим отношение включения
⊂. Это отношение рефлек-
сивно: A
i
⊂ A
i
(множество A
i
включает само себя). Если A
i
⊂ A
j
и
A
j
⊂ A
i
, то A
i
= A
j
, следовательно отношение антисимметрично,
если A
i
⊂ A
j
и A
j
⊂A
k
, то A
i
⊂ A
k
, то есть отношение
⊂ транзитив-
но и является отношением упорядоченности
≤. Множество А с
заданным на нем отношением упорядоченности
≤ называется
упорядоченным этим отношением. Отношение включение явля-
ется частично упорядоченным множеством.
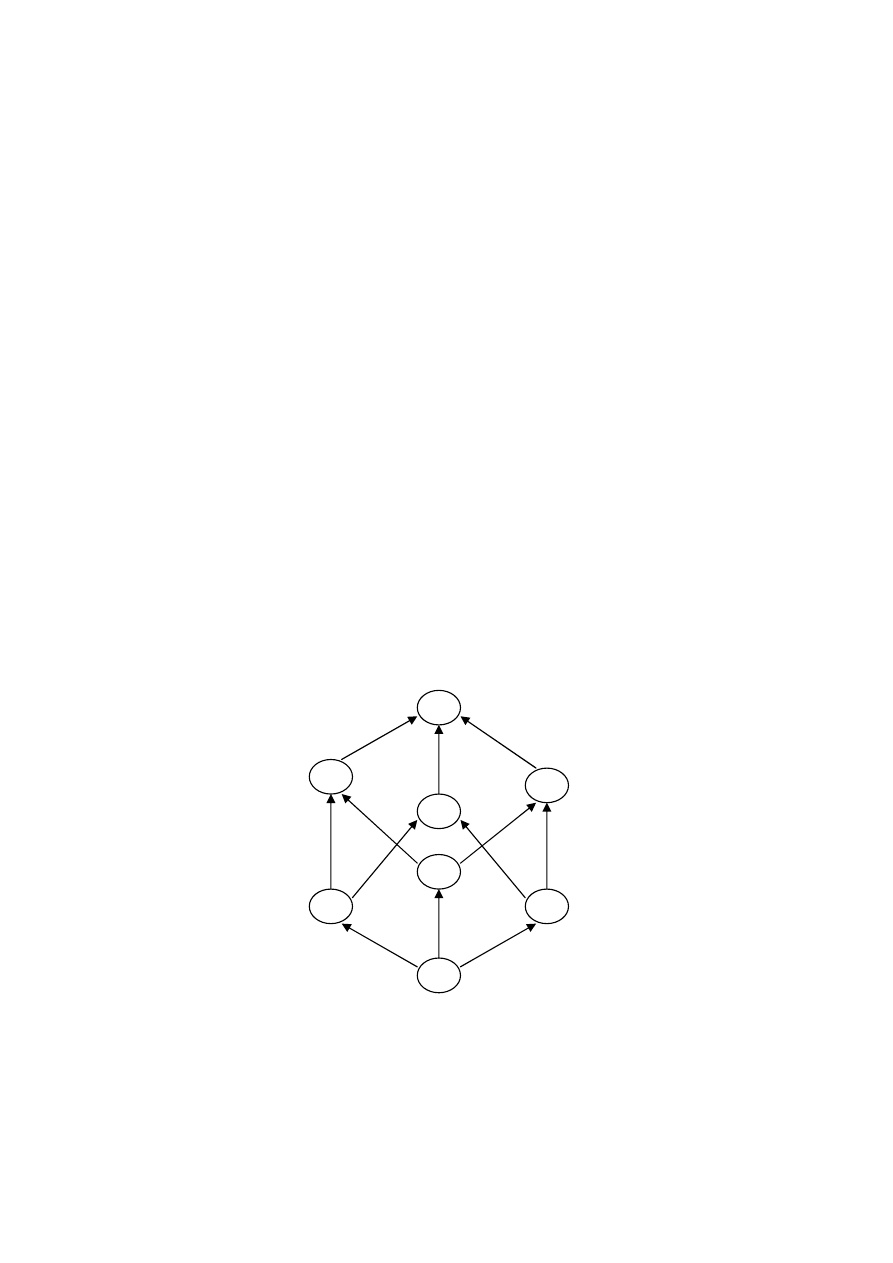
Частично упорядоченное множество изображают в виде
графов G = (X, U). Например, пусть А = {1, 2, 3}. Рассмотрим от-
ношение быть подмножеством. Получаем следующую диаграмму
(удалены петли и транзитивно замыкающие дуги), называемую
диаграммой Хассе Н.
Рисунок 2.12 – Пример диаграммы Хассе
∅
{1}
{2}
{3}
{1,2}
{2,3}
{1,3
{1,2,3}

29
Понятие непосредственного старшего легко задается в час-
тично упорядоченном множестве следующим определением: a
i
покрывает a
j
. Это означает, что a
j
< a
i
и не найдется такого эле-
мента а
k
, что a
j
< a
k
< a
i
. Если рассмотрим подмножество A’
⊂ A и
найдем такой элемент a
L
∈A, что a
i
< a
L
для любого элемента
a
i
∈A’, то этот элемент называется
мажорантой
подмножества
A’. Аналогично, если найдется элемент a
β
∈A, такой, что a
β
< a
j
для любого элемента a
j
∈ A’, то элемент a
β
называется
миноран-
той
подмножества A’.
Если отношение
R
, определенное на множестве
А
, является
рефлексивным, симметричным и транзитивным, то его называют
отношением эквивалентности
.
Классом эквивалентности
, порожденным элементом
х
, на-
зывается подмножество множества
Х,
состоящее из тех элемен-
тов
у
∈
Х
, для которых
х R y
. Класс эквивалентности, порожден-
ный через
х
, обозначается
[x].
Например, дано множество A = {0, 1, 2, 3}. Определим от-
ношение R, отвечающее общепринятому понятию «равно». E =
={<0, 0>, <1,1>, <2,2>, <3,3>}. Для заданного отношения эквива-
лентности Е существуют четыре класса эквивалентности [0] =
={0}, [1] = {1}, [2] = {2}, [3] = {3}.
Отношение принадлежности к одной студенческой группе
на множестве студентов института – это отношение эквивалент-
ности, и классом эквивалентности является множество студентов
одной группы.
Необходимо заметить, что класс эквивалентности порожда-
ется любым своим элементом. Классы эквивалентности, соответ-
ствующие отношению эквивалентности R, определенному на
множестве А, разбивают множество А на конечное число непус-
тых непересекающихся множеств.
Например
, определим отношение R на множестве нату-
ральных чисел следующим образом:
а R b справедливо, если и только если |a – b| делится на 5 без
остатка. В этом случае множество N разбивается на пять беско-
нечных классов эквивалентности:
{{1,6,11,…}, {2,7,12,…}, {3,8,13,…}, {4,9,14,…}, {5,10,15}}.
30
Если
R
– произвольное отношение, определенное на множе-
стве
А
, то его
рефлексивным замыканием
называется наимень-
шее рефлексивное отношение, определенное на множестве А, для
которого отношение R является подмножеством.
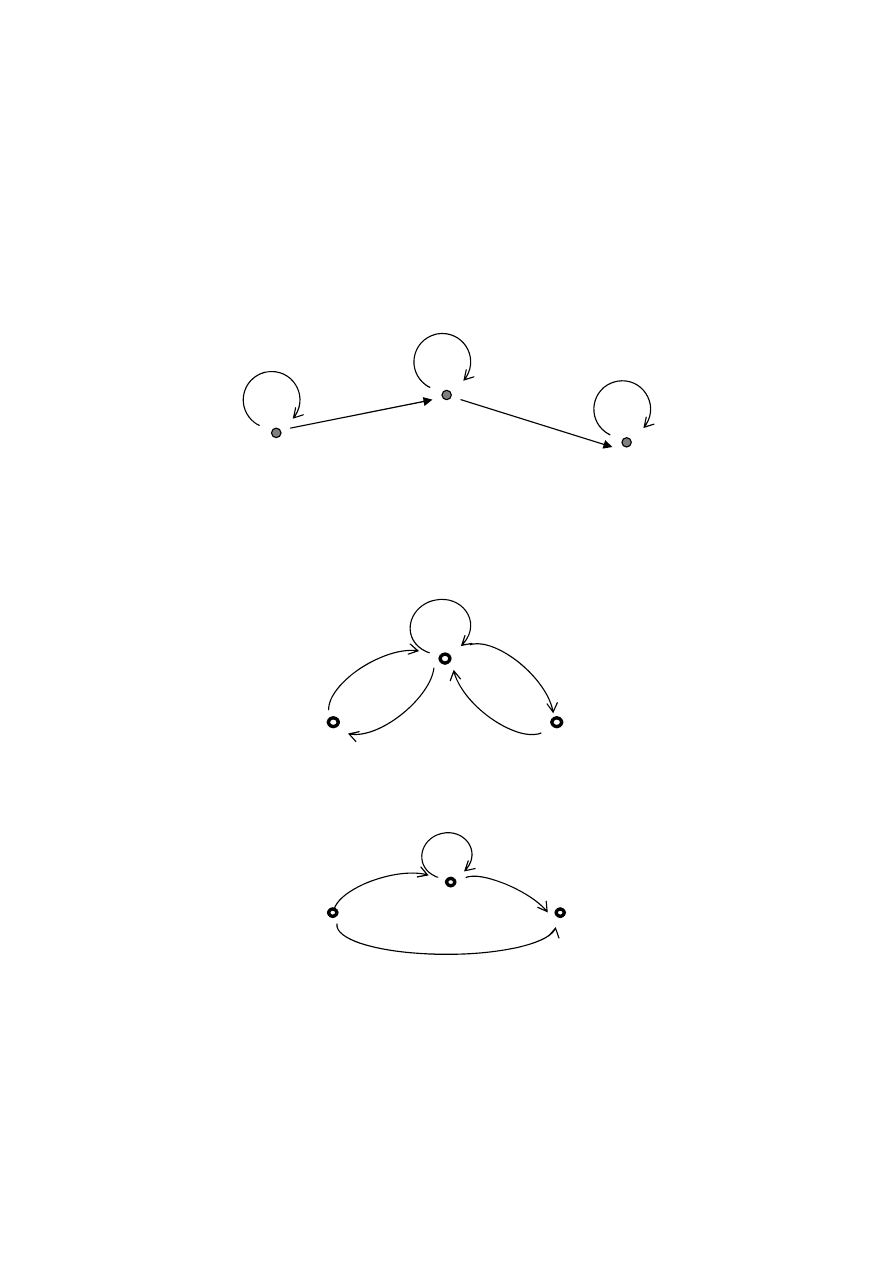
Например, если R = {<0,1>, <1,1>, <1,2>} – отношение, оп-
ределенное на множестве A = {0,1,2}, то его рефлексивным за-
мыканием является множество {<0,0>, <0,1>, <1,1>, <1,2>,
<2,2>}.
Рисунок 2.13 – Рефлексивное замыкание
Симметричным замыканием является множество {<0,1>,
<1,0>, <1,1>, <1,2>, <2,1>}.
Рисунок 2.14 – Транзитивное замыкание {<0,1>, <0,2>, <1,1>, <1,2>}
Рисунок 2.15 – Симметричное замыкание
Заметим, что рефлексивным замыканием отношения <, оп-
ределенного на множестве целых чисел, является отношение
≤,
его симметричным замыканием является отношение
≠, а транзи-
тивным замыканием является само отношение <.
0
1
2
1
2
0
1
2
0