ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6756
Скачиваний: 28
61
2.
«Три дома и три колодца». Три поссорившихся соседа имеют три
общих колодца. Можно ли провести непересекающиеся дорожки
от каждого дома к каждому колодцу?
3.
Найдите число частичных графов конечного графа с m ребрами.
4.
Каково число ребер в полном неориентированном графе с n вер-
шинами?
5.
Пусть U – множество положительных целых чисел, на котором
задано отношение «a есть делитель b». Постройте граф этого от-
ношения для множества целых чисел от 1 до 20.
На рис.2.47 задан граф
отношения «быть сестрой» на
множестве
студентов-
родственников нашего фа-
культета.
Постройте
по
рис.2.47 граф отношения
«быть братом».
6.
Постройте графы отноше-
ний для задач №№ 11 – 17
главы 1.
7.
Постройте матрицы смежности и инциденций для правильных
многогранников: тетраэдра, куба, октаэдра. Найдите для каждого
из них число внутренней устойчивости, число внешней устойчи-
вости, центр, периферийные вершины, радиус, диаметр.
8.
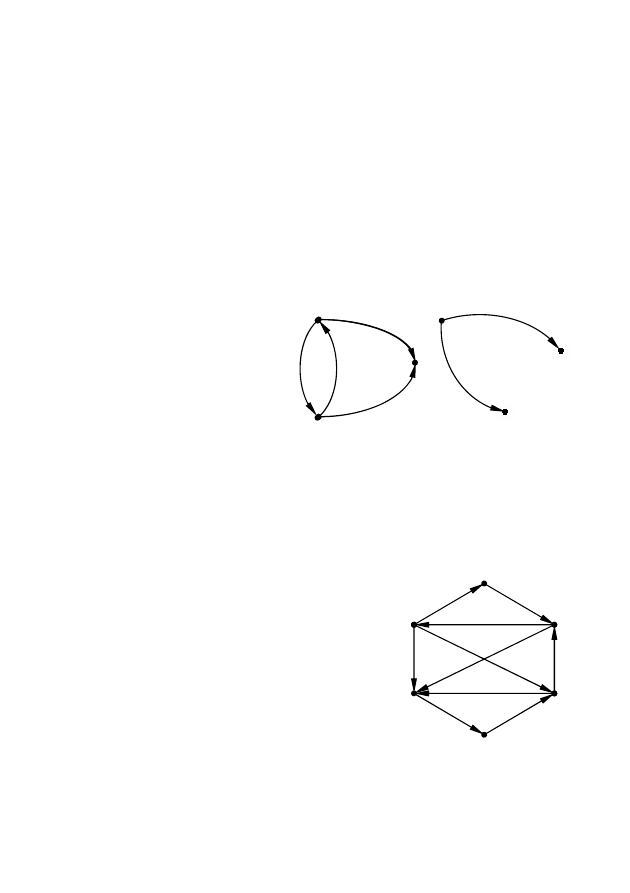
Для графа, изображенного на рис.2.48 найдите:
а) матрицу смежности (вершин);
б) матрицу инциденций;
в) наибольшее внутренне устойчивое
множество;
г) наименьшее внешне устойчивое мно-
жество;
д) матрицу отклонений;
е) вектор отклоненностей;
ж) центр и радиус графа.
10.
Постройте графы, для которых радиус r
равен 2, 3, и такие графы, для которых
диаметр d равен 2, 3.
11.
Определите, какие из графов трех пра-
А
Д
Г
Б
В
Е
Рис. 2.47 – К задаче 6
Рис. 2.48 – К задаче 9
x
6
x
1
x
2
x
3
x
4
x
5
g
10
g
1
g
2
g
8
g
4
g
9
g
3
g
5
g
7
g
6

62
вильных многогранников (тетраэдр, куб, откаэдр) имеют эйлеро-
вы циклы. В тех случаях, когда эйлерова цикла нет, определите,
сколько требуется цепей, чтобы покрыть все ребра.
12.
Какие из графов правильных многогранников имеют гамильто-
новы цепи и циклы?
3.
ОСНОВЫ
МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
3.1
Алгебра
высказываний
Изучение математической логики мы начнём с изучения алгеб-
ры высказываний, на которой базируются другие логические исчис-
ления (логика предикатов, вероятностная логика и т. д.). Алгебра
высказываний представляет и самостоятельный интерес, как основа
для построения моделей, описывающих некоторые дискретные уст-
ройства.
Под высказыванием понимается повествовательное предло-
жение, о котором имеет смысл говорить, что оно истинно или лож-
но, но не то и другое вместе.
Примеры. 1. Волга впадает в Каспийское море.
2. Два больше трёх.
3. Я лгу.
Примеры 1, 2 являются высказываниями (1 – истинно, 2 –
ложно). 3 – не высказывание (если предположить, что оно истинно,
то в силу его смысла оно одновременно ложно и, наоборот, из лож-
ности этого предложения вытекает его истинность).
В алгебре высказываний не рассматривают внутреннюю струк-
туру высказываний, а ограничиваются рассмотрением их свойства
представлять истину или ложь. Поэтому на высказывание можно
смотреть, как на величину, которая может принимать только одно из
двух значений «истина» или «ложь».
Высказывания будем обозначать буквами A, B, C,..., а их зна-
чения, то есть истину или ложь, соответственно цифрами 1 или 0.
В обычной речи сложные предложения образуются из простых
с помощью связок: «и», «или», «если…, то» и др.
Примеры. 1.
Светит солнце, и идёт дождь.
2. Шесть делится на два или шесть делится на
три.
3. Если контакт замкнут, то лампа горит.

63
Связки можно рассматривать как операции над высказывания-
ми. В обычной речи не всегда удаётся однозначно определить ис-
тинность или ложность сложного высказывания по истинности или
ложности его составных частей. В алгебре высказываний вводят
операции, аналогичные связкам обычной речи, причём истинность
или ложность сложного высказывания полностью определяется
истинностью или ложностью его составляющих.
Пусть даны два произвольных высказывания А и В.
1.
Выражение А ٨ В (читается: «А и В») означает высказыва-
ние, истинное только в том случае, когда А и В истинны. Такое вы-
сказывание называют конъюнкцией высказываний А и В. Симво-
лом ٨ обозначают операцию конъюнкции. Эта операция соответст-
вует союзу «и» в обычной речи. Однако в повседневной речи не
принято соединять союзом «и» два высказывания, далекие по со-
держанию. В алгебре же высказываний операция конъюнкции мо-
жет быть применена к любым двум высказываниям. Так, например,
для высказываний «пять больше трех» и «трава зеленая» их конъ-
юнкция «пять больше трех и трава зеленая» является истинным вы-
сказыванием.
2.
Выражение А ٧ В (читается: «А или В») означает высказы-
вание, истинное, если хотя бы одно из высказываний А или В явля-
ется истинным. Такое высказывание называют дизъюнкцией вы-
сказываний А и В. Символ ٧ обозначает операцию дизъюнкции.
Эта операция соответствует союзу или обычной речи, применяе-
мому в неисключающем смысле.
Дело в том, что в повседневной речи союз «или» может иметь
два смысловых значения: неисключающее и исключающее. В пер-
вом случае подразумевается, что из двух высказываний, по крайней
мере, одно истинно, а может быть и оба истинны. Примером являет-
ся высказывание «В жаркую погоды пьют воду или едят мороже-
ное». Во втором случае полагают, что из двух высказываний истин-
ным является только одно («Сегодня мы поедем на экскурсию или
пойдем на пляж»). Конъюнкция высказываний соответствует перво-
му случаю.
3.
Выражение А
→ В (читается: «если А, то В» или «А влечет
В») означает высказывание, которое ложно тогда и только тогда,
когда А истинно, а В ложно. Такое высказывание называют импли-
кацией высказываний А и В. Высказывание А называется услови-

64
ем или посылкой, высказывание В – заключением или следствием
импликации. Символ
→ обозначает операцию импликации. В
обычной речи операции импликации соответствует связка если ...,
то. Отличие состоит в том, что связка предполагает смысловую за-
висимость соединяемых высказываний, а для операции
→ смысло-
вая связь несущественна. Так, например, высказывания «если
2
∗2 = 5, то трава синяя» и «если два больше трех, то восемь делится
на четыре» являются истинными, так как у первого из них ложная
посылка, а у второго – истинное следствие. Импликация «если
2
∗2 = 4, то 5<2» ложна, поскольку ее условие истинно, а заключение
ложно.
4.
Выражение А
∼ В (читается: «А эквивалентно В», «для то-
го, чтобы А, необходимо и достаточно, чтобы В», «А тогда и только
тогда, когда В», «А равносильно В») означает высказывание, кото-
рое истинно тогда и только тогда А и В оба истинны или оба ложны.
Такое высказывание называют эквивалентностью высказываний
А и В. Символ
∼ означает операцию эквивалентности. В обычной
речи этой операции соответствует связка тогда и только тогда,
когда. Примером эквивалентности может служить высказывание
«Треугольник АВС равнобедренный тогда и только тогда, когда
угол при вершине В равен углу при вершине С».
5.
Выражение
⎯А (читается: «не А») означает высказывание,
которое истинно, когда А ложно и ложно, когда А истинно. Такое
высказывание
называют
отрицанием
высказывания
А.
Символ
⎯ над буквой обозначает операцию отрицания. В обычной
речи этой операции соответствует частица не. Например, для истин-
ного высказывания «восемь делится на четыре» отрицанием являет-
ся ложное высказывание «неверно, что восемь делится на четыре»
или «восемь не делится на четыре».
Если А, В, С – произвольные высказывания, которые рассмат-
риваются как величины, принимающие одно из двух значений 1 или
0, то, применяя к ним операции конъюнкции, дизъюнкции, импли-
кации, эквивалентности и отрицания, можно получить новые слож-
ные высказывания, например:
((А ٧ В) ٨
⎯С) → A →
B.
(3)
В обычной речи не всегда удается однозначно определить ис-
тинность или ложность сложного высказывания по истинности или
ложности его составных частей. В алгебре высказываний значение
65
сложного высказывания полностью определяется значениями его
составляющих. Предположим, что А – ложное высказывание, В –
истинное, С – ложное. Тогда высказывание (3) является ложным в
силу определения логических операций.
Наряду с высказываниями, принимающими определенные и
постоянные значения 1, 0 и называемыми определенными выска-
зываниями, в алгебре высказываний рассматривают переменные
высказывания, которые не имеют определённого значения. Если
X, Y, Z – переменные высказывания, то, применяя к ним операции
конъюнкции, дизъюнкции, импликации, эквивалентности и отрица-
ния, можно получить формулы алгебры высказываний. При задании
значений переменных высказываний формула принимает опреде-
ленное значение. Таким образом, каждая формула определяет неко-
торую функцию, переменными которой являются переменные вы-
сказывания. Переменные и функции принимают только два значе-
ния: истина или ложь, поэтому функции можно описать конечной
таблицей, которую называют истинностной таблицей или табли-
цей истинности данной формулы.
Приведём истинностную таблицу формул X ٨ Y, X ٧ Y,
X
→ Y,
X
∼ Y,⎯X (табл.3.1).
Таблица 3.1 – Истинностная таблица для операций над высказыва-
ниями
X Y X ٨ Y X
٧ Y X
→ Y
X
∼ Y
⎯X
0
0 0 0 1 1 1
0
1 0 1 1 0 1
1
0 0 1 0 0 0
1
1 1 1 1 1 0
Возможен случай, когда две формулы имеют одну и ту же ис-
тинностную таблицу. Такие формулы называют равносильными.
При этом количество и состав переменных в формулах не обяза-
тельно должны совпадать. Так, например, равносильными являются
формулы
⎯Y ٧Z и
((X ٧ Y) ٨
⎯Z) → (X → Y) (табл. 3.2).