ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6753
Скачиваний: 28
66
Запись формул можно упростить, опуская некоторые скобки и
считая, что если их нет, то выполнять операции нужно в следующем
порядке:
1)
отрицание;
2)
конъюнкция;
3)
дизъюнкция;
4)
импликация;
5)
эквивалентность.
Например, формулу X ٨ Y ٧ Z следует понимать как
(X ٨ Y) ٧ Z.
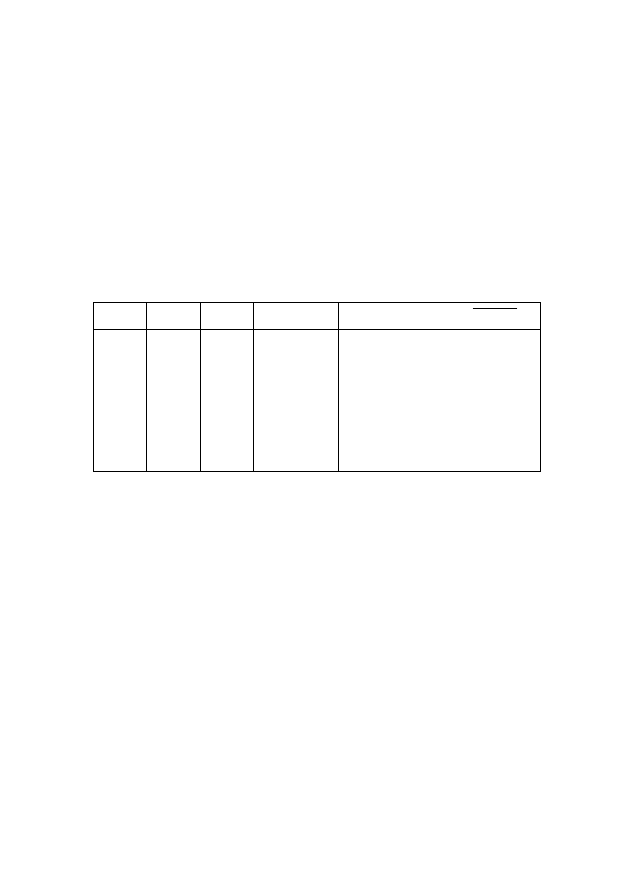
Таблица 3.2 – Истинностная таблица для равносильных формул
X Y Z
⎯Y ٧ Z
((X ٧ Y) ٨
⎯Z) → (X → Y)
0 0 0
1
1
0 0 1
1
1
0 1 0
0
0
0 1 1
1
1
1 0 0
1
1
1 0 1
1
1
1 1 0
0
0
1 1 1
1
1
Если все значения формулы в истинностной таблице равны 1,
то формула называется тождественно истинной или тавтологией.
Тавтологии называют также законами логики. В обычном языке
рассуждение имеет импликативную форму «если то-то и то-то, то
то-то и то-то». При этом заботятся не об истинности или ложности
посылок и заключений, а о правильности рассуждений. Рассуждения
должны быть правильными, то есть соответствующие им имплика-
ции должны быть тождественно истинными. С этой точки зрения
задачей логики можно считать исследование тавтологий. Тавтоло-
гичность формулы можно всегда обнаружить с помощью таблиц
истинности.
3.2
Булевы
функции
Функция f (x
1
, x
2
,..., x
n
), принимающая два значения: 0 и 1 и за-
висящая от переменных, каждая из которых может принимать зна-
чения 0 и 1, называется булевой или переключательной. Из опре-

67
деления следует, что область определения булевой функции – сово-
купность всевозможных n-мерных наборов из нулей и единиц, а для
её задания достаточно указать, какие значения функции соответст-
вуют каждому из наборов (табл. 3.3).
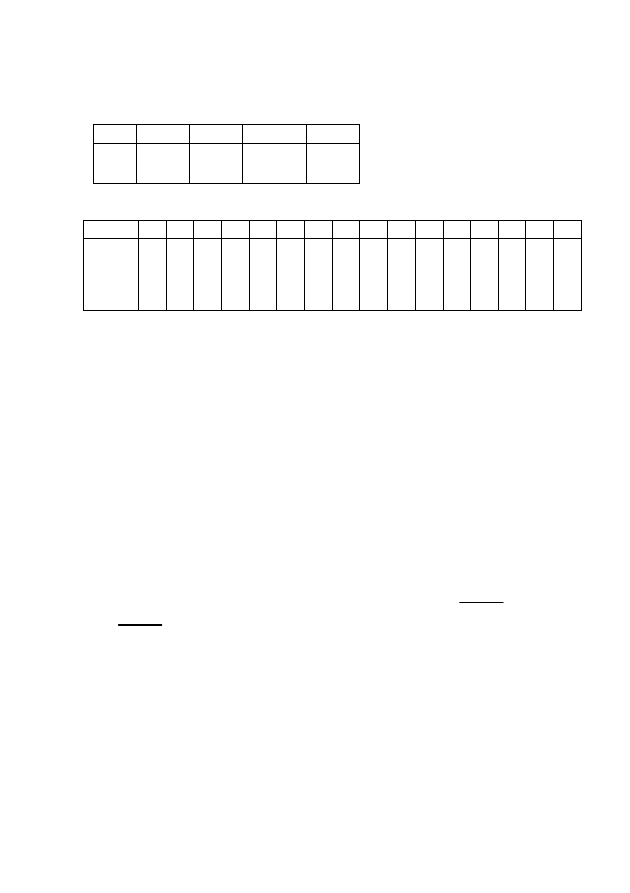
Таблица 3.3 – Задание булевой функции
x
1
x
2
... x
n-1
x
n
f
(x
1
, x
2
,...,x
n-1
, x
n
)
0
0
...
0
0
f (0, 0,...,0, 0)
0
0
...
0
1
f (0, 0,...,0, 1)
... ... ... ... ... .................………
1
1
...
1
0
f (1, 1,...,1, 0)
1
1
...
1
1
f (1, 1,...1, 1)
Порядок расположения наборов, принятый в таблице, называ-
ется стандартным или естественным. При таком порядке каждому
набору
α = (α
1
,...,
α
n
), где
α
i
есть 0 или 1, ставится в соответствие число
N =
α
1
2
n-1
+ ... +
α
n-1
2 +
α
n
.
Наборам (0, 0,...,0, 0), (0, 0,...,0, 1),..., (1, 1,...,1, 1) соответствуют
числа 0, 1,..., 2
n
-1. Естественным порядком будет расположение на-
боров в порядке возрастания соответствующих им чисел. Десятич-
ное число, соответствующее входному набору, является его номе-
ром. Поэтому очевидно, что количество k входных наборов для бу-
левой функции n переменных равно k=2
n
. Количество же различных
функций n переменных можно определить из следующих соображе-
ний. Каждая функция задается набором своих k значений (для k
входных наборов), которому также можно поставить в соответствие
k-разрядное двоичное число. Располагая теперь в таблице функции в
порядке возрастания соответствующих им чисел, мы получим все
возможные различные функции. Количество таких функций будет
равно
n
k
2
2
2
=
.
Рассмотрим другие способы задания булевых функций. Снача-
ла познакомимся с функциями одной и двух переменных, которые
часто употребляются в математической логике и кибернетике, их
можно считать «элементарными» функциями (табл. 3.4, 3.5).
68
Таблица 3.4 – Булевы функции одной переменной
x g
1
(x) g
2
(x) g
3
(x) g
4
(x) g
1
(x), g
4
(x) – константы 0 и 1,
0 0 0 1 1
g
2
(x) = x,
1 0 1 0 1
g
3
(x) =
⎯x (отрицание x).
Таблица 3.5 – Булевы функции двух переменных
x
1
x
2
f
1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
f
9
f
10
f
11
f
12
f
13
f
14
f
15
f
16
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
Следует отметить, что к функциям двух переменных относятся
и такие, которые в действительности зависят от одной переменной
или не зависят ни от одной.
Функции f
1
, f
16
– константы 0 и 1. Они не зависят существенно
ни от одной переменной.
Функции f
4
= х
1
, f
11
=
⎯х
2
, f
6
= х
2
, f
13
=
⎯х
1
зависят существенно
только от одной переменной.
f
2
= х
1
٨ х
2
– конъюнкция или логическое умножение (знак
«٨» можно заменять на «·», либо опускать).
f
8
= х
1
٧ х
2
– дизъюнкция или логическое сложение.
f
10
– эквивалентность, х
1
∼ х
2
.
f
7
= х
1
⊕
х
2
или х
1
+ х
2
(mod 2) – сложение по модулю два.
f
12
, f
14
– импликация, х
2
→ х
1
и х
1
→
х
2.
f
15
– штрих Шеффера, х
1
| х
2.
f
9
– стрелка Пирса, х
1
↓ х
2
(другое название – функция Вебба).
f
3
, f
5
– функции запрета х
1
и х
2
соответственно. f
3
= х
1
→ х
2
,
f
5
= х
2
→ х
1
.
Исходя из элементарных функций можно строить формулы, т.е.
рассматривать функции от функций например, (x
1
⊕ x
2
)
⎯х
2
)
→ х
3
.
Некоторые свойства элементарных функций
1.
Функции конъюнкция, дизъюнкция, сумма по модулю 2 обла-
дают свойством ассоциативности, что позволяет опускать скоб-
ки и использовать следующие обозначения:

69
n
n
٨ x
i
= x
1
x
2
... x
n
,
٧ x
i
= x
1
٧ x
2
٧...٧ x
n
,
i=1
i=1
2.
х
1
х
2
=
⎯х
1
٧
⎯х
2
, х
1
٧ х
2
=
⎯х
1
⎯х
2
– закон де Моргана,
x
x
=
– закон двойного отрицания.
3.
х х = х, х ٧ х = х, х
⎯х = 0, х ٧⎯х = 1,
х 0 = 0, х 1 = х, х ٧ 0 = х, х ٧ 1 = 1.
Свойства можно проверить по таблице булевых функций
(табл. 3.5).
3.3
Совершенные
дизъюнктивная
и
конъюнктивная
нормальные
формы
Рассмотрим возможность представления произвольной булевой
функции в виде формулы из элементарных функций. Так, теоремы 1
и 2 доказывают возможность такого представления в виде формулы,
содержащей только функции дизъюнкции, конъюнкции и отрицания.
Теорема 1. Произвольную булеву функцию f (x
1
,x
2
...,x
n
) можно
представить в виде
σ=(1,...,1)
f (x
1
,x
2
...,x
n
) =
٧
f (
σ
1
,
σ
2
...,
σ
n
) х
1
σ
1
х
2
σ
2
... х
n
σ
n
,
(4)
σ=(0,...,0)
где
σ
i
∈ {0, 1}, x
i
0
=
⎯x
i
, x
i
1
= х
i
,
σ = (σ
1
,...,
σ
n
) и дизъюнкция берётся
по всем n-мерным наборам из нулей и единиц.
Доказательство. Покажем, что левая и правая части соотно-
шения (4) совпадают. Произвольный набор
α = (α
1
,
α
2
,...,
α
n
), где
каждое
α
i
∈ {0,1}, подставим в соотношение (4). В левой части по-
лучим f (
α
1
,
α
2
,..,
α
n
), а в правой части
σ=(1,...,1)
٧
f(
σ
1
,
σ
2
,...,
σ
n
)
α
1
σ
1
α
2
σ
2
...
α
n
σ
n
= f(
α
1
,
α
2
,...,
α
n
)
α
1
α
1
α
2
α
2
...
α
n
α
n
=
σ=(0,...,0)
= f (
α
1
,
α
2
,...,
α
n
) .
Равенства в правой части вытекают из свойств конъюнкции, дизъ-
юнкции и из того, что х
σ
= 1
⇔ x = σ. ■

70
Если f (x
1
, x
2
,...,x
n
)
≢ 0, то соотношение (4) можно переписать
в форме
f (x
1
, x
2
...,x
n
) =
٧
х
1
σ
1
х
2
σ
2
⋅⋅⋅х
n
σ
n
(5)
по всем
σ
f (
σ)=1
Эта форма называется совершенной дизъюнктивной нормальной
формой (совершенной ДНФ) функции f (x
1
,x
2
,...,x
n
).
Построение совершенной ДНФ из табличного задания функ-
ции производится следующим образом. Для каждого набора
σ = (σ
1
,...,
σ
n
) такого, что f (
σ
1
,...,
σ
n
) = 1, составляется выражение
х
1
σ
1
⋅⋅⋅х
n
σ
n
и затем все такие конъюнкции соединяются знаком дизъ-
юнкции. Например, для функции сложения по модулю два совер-
шенная ДНФ имеет вид
х
1
⊕ х
2
=
⎯х
1
х
2
٧ х
1
⎯x
2
.
Теорема 2. Произвольную булеву функцию f (x
1
,x
2
,...,x
n
) можно
представить в виде
σ=(1,...,1)
f (x
1
,x
2
,...,x
n
) =
٨
(f (
σ
1
,
σ
2
...,
σ
n
) ٧ х
1
⎯
σ
1
٧ х
2
⎯
σ
1
٧...٧ х
n
⎯
σ
n
)
, (6)
σ=(0,...,0)
где
σ
i
= {0,1}, x
i
0
=
⎯x
i
, x
i
1
= х
i
,
σ = (σ
1
,...,
σ
n
) и конъюнкция берётся
по всем n-мерным наборам из нулей и единиц.
Доказательство. Из свойства булевой функции (закон двойно-
го отрицания) имеем f (x
1
,...,x
n
) =
f
(x
1
,...,x
n
).
Для функции
⎯f (x
1
,...,x
n
) по теореме 1 существует представле-
ние в виде
σ=(1,...,1)
⎯f (x
1
,x
2
,...,x
n
) =
٧
⎯f (σ
1
,
σ
2
,...,
σ
n
) х
1
σ
1
х
2
σ
2
...х
n
σ
n
, тогда
σ=(0,...,0)
σ= (1,...,1)
f (x
1
,x
2
,...,x
n
) =
٧
⎯f (σ
1
,
σ
2
,...,
σ
n
) х
1
σ
1
х
2
σ
2
...х
n
σ
n
=
σ=(0,...,0)
σ=(1,...,1)
=
٨
(f (
σ
1
,
σ
2
,...,
σ
n
) ٧ x
1
σ
1
٧ x
2
σ
2
٧...٧ x
n
σ
n
), что следует из
σ=(0,...,0)