ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6757
Скачиваний: 28

56
P
1
= P(x
i
, x
j
)
∪ P′ ∪ P(x
j
, x
i
),
который возвращается в x
i
и содержит больше ребер, чем P. Если P
1
не является эйлеровым циклом, то построение повторяется. По
окончании построения получим эйлеров цикл. ■
Процесс построения эйлерова цикла иллюстрирует рис. 2. 44, б.
Объединяя, например, циклы {x
1
, x
2
, x
3
, x
4
, x
5
, x
6
, x
1
} и {x
3
, x
7
, x
8
, x
3
,
x
5
, x
1
, x
3
}, получим эйлеров цикл { x
1
, x
2
, x
3
, x
7
, x
8
, x
3
, x
5
, x
1
, x
3
, x
4
, x
5
,
x
6
, x
1
}.
Как граф с эйлеровым циклом можно рассмотреть схему обхо-
да выставки по различным коридорам, которую посетители должны
пройти согласно указателям так, чтобы увидеть каждый экспонат по
одному разу.
Эйлеровой цепью называется цепь, включающая все ребра
данного конечного неориентированного графа G(X), но имеющая
различные начало х
i
и конец х
j
. Чтобы в графе существовала эйлеро-
ва цепь, он должен быть связным и все вершины, кроме х
i
и х
j
долж-
ны иметь четные степени. Степени вершин х
i
и х
j
должны быть не-
четными, что естественно, так как из х
i
мы лишний раз выходим, а в
х
j
мы лишний раз входим. Эти условия являются достаточными
для существования эйлеровой цепи.
Важен также следующий вопрос: каково наименьшее количе-
ство не пересекающихся по ребрам цепей, покрывающих конеч-
ный связный граф G(X) (покрыть – значит включить все ребра графа
в цепь)? На этот вопрос отвечает теорема 2.
Теорема 2. В конечном связном неориентированном графе
G(X) с k вершинами нечетной степени минимальное число непере-
секающихся по ребрам цепей, покрывающих G(X) равно k/2.
Доказательство. Пусть G(X) не является эйлеровым графом и
k – число его вершин нечетной степени. Ранее было доказано, что k
четно. Каждая вершина нечетной степени должна быть концом хотя
бы одной из покрывающих граф цепей. Следовательно, число таких
цепей не меньше, чем k/2. Но можно показать, что и не больше. Со-
единим попарно вершины нечетной степени k/2 ребрами. Тогда сте-
пень каждой вершины увеличиться на единицу и станет четной. По-
лучится эйлеров граф, в котором существует эйлеров цикл. Теперь
будем постепенно выбрасывать присоединенные ребра. При выбра-
сывании первого ребра эйлеров цикл превратится в эйлерову цепь, а
при выбрасывании каждого последующего ребра одна из возникших
57
к этому моменту цепей разобьется на две части. Таким образом, об-
щее число этих цепей равно k/2. ■
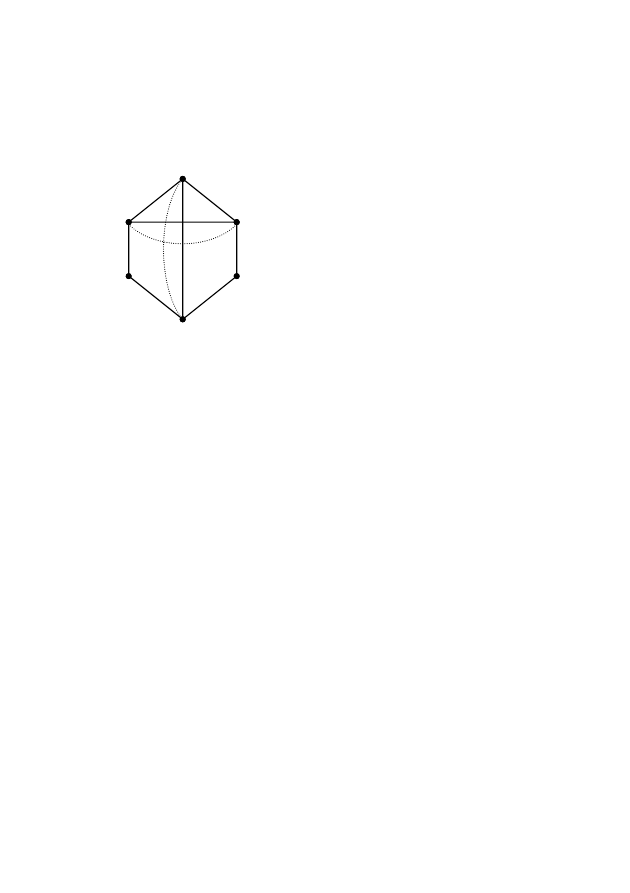
В качестве примера рассмот-
рим граф на рис.2.45. В нем x
1
, x
2
,
x
3
, x
5
– вершины нечетной степени.
Добавим два ребра: (x
2
, x
5
), (x
1
, x
3
)
(штриховые линии). Получим эй-
леров граф с эйлеровым циклом
{x
1
, x
2
, x
3
, x
4
, x
5
, x
2
, x
5
, x
6
, x
1
, x
3
, x
1
}.
Убрав (x
3
, x
1
), получим эйлерову
цепь. Убрав (x
2
, x
5
), получим 2 по-
крывающих цепи: {x
1
, x
2
, x
3
, x
4
, x
5
,
x
2
} и {x
5
, x
6
, x
1
, x
3
}.
Из теоремы 2 следует, что ес-
ли в связном неориентированном
мультиграфе имеются две вершины
нечетной степени х
i
и х
j
, то сущест-
вует эйлерова цепь, начинающаяся в х
i
и кончающаяся в х
j
.
Если связный мультиграф G(X) имеет четыре вершины нечет-
ной степени, то его можно нарисовать двумя росчерками. Если ко-
личество нечетных степеней равно k, то граф можно нарисовать k/2
росчерками.
Рассмотрим теперь случай конечного ориентированного гра-
фа. Чтобы в конечном ориентированном графе существовал эйлеров
цикл (контур), необходимо и достаточно, чтобы полустепени исхо-
да и захода вершин этого графа по входящим и исходящим дугам
были равны:
m
′(x
i
) = m
′′(x
i
),
∀ x
i
∈ X.
Доказательство то же, что и для неориентированного графа.
Так как любому неориентированному графу соответствует ори-
ентированный, в котором каждое ребро заменено двумя дугами, ин-
цидентными тем же вершинам и идущими в противоположном на-
правлении, то отсюда следует, что в конечном связном графе все-
гда можно построить ориентированный цикл, проходящий че-
рез каждое ребро по одному разу в каждом из двух направлений.
Такой цикл называется способом обхода всех ребер графа. Он ис-
пользуется во многих прикладных задачах, связанных с графами.
x
2
x
3
x
4
x
5
x
6
x
1
Рис. 2.45 – Пример построе-
ния покрывающих цепей

58
2.8.2
Гамильтоновы
цепи
,
циклы
,
пути
,
контуры
Гамильтоновой цепью в неориентированном графе называет-
ся цепь, проходящая через каждую его вершину один и только один
раз.
Гамильтоновым циклом в неориентированном графе назы-
вается цикл, проходящий через каждую вершину один и только
один раз за исключением начальной вершины, которая совпадает с
конечной.
Гамильтоновым путем в ориентированном графе называется
путь S(x
1
, …, x
n
), проходящий через все вершины графа, притом
только по одному разу.
Гамильтоновым контуром называется контур М(х
0
, x
1
,…, x
n
,
x
0
) в ориентированном графе G(X), если он проходит через все вер-
шины графа, притом только по одному разу.
Существует следующая распространенная интерпретация зада-
чи о гамильтоновых циклах. Обед накрыт на круглом столе. Среди
гостей некоторые являются друзьями. При каких условиях можно
рассадить всех так, чтобы по обе стороны от каждого из присутст-
вующих сидели его друзья?
В применении графов к играм вершины соответствуют различ-
ным позициям. Существование гамильтонова цикла равносильно
существованию циклической последовательности ходов, содержа-
щей каждую позицию по одному разу. Примером является известная
задача о шахматном коне: можно ли, начиная с произвольного поля
на доске, ходить конем в такой последовательности, чтобы пройти
каждое из шестидесяти четырех полей и вернуться в исходное?
К гамильтоновым циклам относится также известная задача о
бродячем торговце (задача о коммивояжере). Район, который дол-
жен посетить коммивояжер, содержит определенное количество
городов. Расстояния между ними известны, и нужно найти кратчай-
шую дорогу, проходящую через все пункты и возвращающуюся в
исходный. Эта задача имеет ряд приложений в экономике и иссле-
довании операций.
Сформулирован целый ряд достаточных условий существова-
ния гамильтоновых цепей, циклов, путей и контуров. Приведем не-
которые из них без доказательства.

59
1. Теорема Кёнига. В полном конечном графе всегда существу-
ет гамильтонов путь.
2. Если в графе G(X) с n вершинами для любой пары вершин х
i
и х
j
справедливо неравенство
m(x
i
) + m(x
j
)
≥ n – 1,
где m(x
i
), m(x
j
) – степени вершин х
i
и х
j
, то граф G(X) имеет гамиль-
тонову цепь.
Несмотря на сходство в определении эйлерова и гамильтоново-
го циклов, соответствующие теории для этих понятий имеют мало
общего. Критерий существования для эйлеровых циклов был уста-
новлен просто, для гамильтоновых циклов никакого общего правила
неизвестно. Более того, иногда даже для конкретных графов бывает
трудно решить, можно ли найти такой цикл. В принципе, поскольку
речь идет о конечном числе вершин, задачу можно решить перебо-
ром, однако эффективного алгоритма неизвестно. Имеются некото-
рые частные схемы для отдельных случаев. Один довольно большой
пример определения кратчайшей воздушной линии, соединяющей
все столицы штатов в США, просчитали Данциг, Джонсон, и Фал-
керсон.
2.9
Характеристики
графов
Решение многих технических задач методами теории графов
сводится к определению тех или иных характеристик графов, поэто-
му полезно знакомство со следующими характеристиками.
Цикломатическое число. Пусть G(X) – неориентированный
граф, имеющий n вершин, m ребер и r компонент связности. Цикло-
матическим числом графа G называется число
ν(G) = m – n + r.
Это число имеет интересный физический смысл: оно равно
наибольшему числу независимых циклов в графе. При расчете элек-
трических цепей цикломатическим числом можно пользоваться для
определения числа независимых контуров.
Хроматическое число. Пусть p – натуральное число. Граф
G(X) называется р-хроматическим, если его вершины можно рас-
красить различными цветами так, чтобы никакие две смежные вер-
шины не были раскрашены одинаково. Наименьшее число р, при
котором граф является р-хроматическим, называется хроматическим
числом графа и обозначается
γ(G). Если γ(G) = 2, то граф называется
60
бихроматическим. Необходимым и достаточным условием того,
чтобы граф был бихроматическим, является отсутствие в нем циклов
нечетной длины.
Хроматическое число играет важную роль при решении задачи
наиболее экономичного использования ячеек памяти при програм-
мировании. Однако его определение, за исключением
γ(G) = 2, пред-
ставляет собой довольно трудную задачу, требующую применения
ЭВМ.
Множество внутренней устойчивости. Множество S
⊆ X
графа G(X) называется внутренне устойчивым, если никакие две
вершины из S не являются смежными, то есть для любого х
∈ S
имеет место
G(x)
∩ S = ∅.
Множество внутренней устойчивости, содержащее наибольшее
число элементов, называется наибольшим внутренне устойчивым
множеством, а число элементов этого множества называется чис-
лом внутренней устойчивости графа G. Наибольшее внутренне
устойчивое множество играет важную роль в теории связи.
Множество внешней устойчивости. Множество T
⊂ X графа
G(X) называется внешне устойчивым, если любая вершина, не при-
надлежащая T, соединена дугами с вершинами из T, то есть для лю-
бого x
∉ T имеет место G(x) ∩ T ≠ ∅.
Множество внешней устойчивости, содержащее наименьшее
число элементов, называется наименьшим внешне устойчивым
множеством, а число элементов этого множества называется чис-
лом внешней устойчивости графа G(X).
2.10
Задачи
и
упражнения
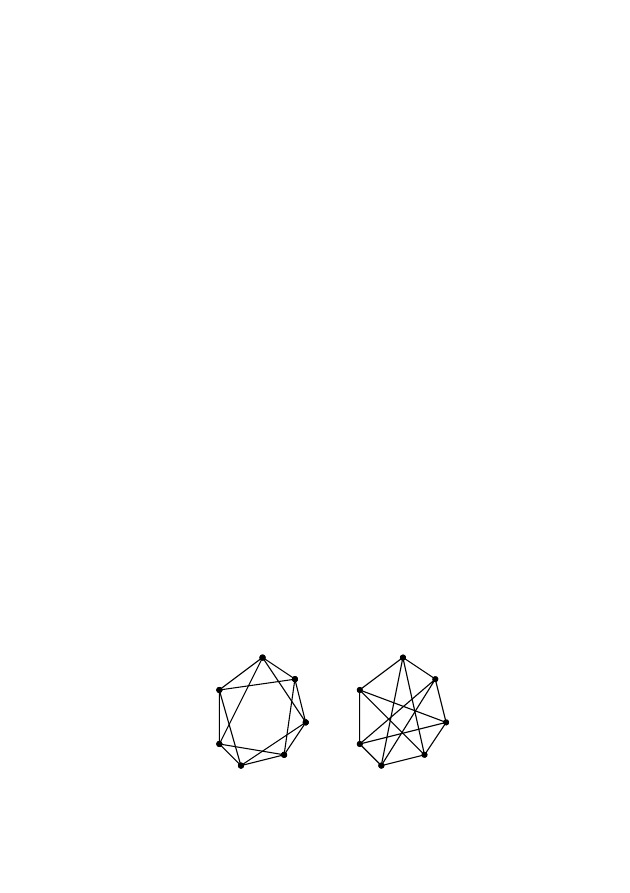
1.
Покажите, что два графа на рис.2.46 изоморфны.
Рис. 2.46 – К задаче 1