ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6749
Скачиваний: 28

81
x
2
x
3
x
4
→⎯x
2
⎯x
4
٧
x
1
x
2
/≡
1, не удовлетворяет следствию.
Импликант
⎯x
1
x
3
x
4
, для которого
⎯x
1
x
3
x
4
→⎯x
2
⎯x
4
٧
x
1
x
2
/≡
1, не удовлетворяет следствию.
Импликант
⎯x
1
⎯x
2
x
3
, для которого
⎯x
1
⎯x
2
x
3
→ ⎯x
2
⎯x
4
٧
x
1
x
2
/≡
1, не удовлетворяет следствию.
Таким образом, последовательность действий при выполнении
второго этапа состоит в следующем:
1)
для каждого простого импликанта сокращённой ДНФ про-
верить, входит он в ядро или нет. Отметить неядерные импликанты;
2)
проверить для отмеченных импликантов выполнение
следствия из теоремы 8. Простые импликанты, для которых выпол-
нено следствие, удалить из сокращённой ДНФ;
3)
проверить возможность удаления оставшихся отмеченных
конъюнкций. Из полученных тупиковых ДНФ выбрать минималь-
ную ДНФ.
Рассмотрим эту последовательность действий на примере 2:
1) нашли ядро функции f (x
1
, x
2
, x
3
, x
4
), состоящее из простых
импликантов
⎯x
2
⎯x
4
и x
1
x
2.
Отметим курсивом в сокращённой ДНФ
неядерные импликанты:
⎯x
2
⎯x
4
٧
x
1
⎯
x
4
٧
x
1
x
2
٧
x
2
x
3
x
4
٧
⎯x
1
x
3
x
4
٧
⎯x
1
⎯
x
2
x
3
;
2) среди помеченных импликантов нашли удовлетворяющий
следствию из теоремы 8. Это импликант x
1
⎯x
4
. Удалим его из со-
кращённой ДНФ:
⎯x
2
⎯x
4
٧
x
1
x
2
٧
x
2
x
3
x
4
٧
⎯x
1
x
3
x
4
٧
⎯x
1
⎯
x
2
x
3
;
3) для получения тупиковых ДНФ удаляем подмножества от-
меченных импликантов. Можно удалить следующие подмножества:
{ x
2
x
3
x
4
,
⎯x
1
x
3
x
4
,
⎯x
1
⎯x
2
x
3
}
I
, { x
2
x
3
x
4
,
⎯x
1
x
3
x
4
}
II
, { x
2
x
3
x
4
,
⎯x
1
⎯x
2
x
3
}
III
,
{
⎯x
1
x
3
x
4
,
⎯x
1
⎯x
2
x
3
}
IV
, { x
2
x
3
x
4
}
V
, {
⎯x
1
x
3
x
4
}
VI
, {
⎯x
1
⎯x
2
x
3
}
VII
.
При каждом удалении нужно проверять, представляет ли оставшаяся
ДНФ функцию f (x
1
, x
2
, x
3
, x
4
).
Если удалить подмножество I, то получим ДНФ, не представ-
ляющую функцию f (x
1
, x
2
, x
3
, x
4
), так как на наборе {0,1,1,1} функ-
ция
f (x
1
, x
2
, x
3
, x
4
), = 1, а
⎯x
2
⎯x
4
٧
x
1
x
2
=0.
Если удалить подмножество II, то получим ДНФ, не представ-
ляющую функцию f (x
1
, x
2
, x
3
, x
4
), так как на наборе {0,1,1,1} функ-
ция

82
f (x
1
, x
2
, x
3
, x
4
), = 1, а
⎯x
2
⎯x
4
٧
x
1
x
2
٧
⎯x
1
⎯x
2
x
3
= 0.
Если удалить подмножество III, получим минимальную ДНФ
функции f (x
1
, x
2
, x
3
, x
4
):
⎯x
2
⎯x
4
٧
x
1
x
2
٧
⎯x
1
x
3
x
4
- минимальная ДНФ.
3.5.3
Минимизация
ДНФ
методом
Квайна
Существуют и другие методы, позволяющие независимо от ис-
ходной формы представления функции найти все ее тупиковые
формы и выбрать из них минимальную. Одним из них является ме-
тод Квайна. В соответствии с этим методом отыскание минимальной
ДНФ проводится в несколько этапов.
Первый этап. Функция, заданная в виде логической формулы
произвольной формы, представляется в совершенной ДНФ. При
этом:
1) последовательным применением эквивалентных преобразо-
ваний логическая функция приводится к ДНФ, то есть к форме, не
содержащей знаков отрицания над функциями, более сложными,
чем один из аргументов;
2) каждый член ДНФ, представляющий собой конъюнкцию ме-
нее n членов (n - количество аргументов функции), развертывается в
дизъюнкцию нескольких элементарных конъюнкций умножением
на выражение вида (x
1
٧
⎯x
1
)(x
2
٧
⎯x
2
)..., тождественно равное едини-
це;
3) приводятся, если возможно, подобные члены.
Второй этап. Отыскиваются все простые импликанты данной
функции. Для этого выписываются все элементарные конъюнкции,
входящие в СДНФ. Каждая из пар этих конъюнкций исследуется на
возможность склеивания. Члены, участвовавшие хотя бы в одном
склеивании, отмечаются, но не исключаются из дальнейших сравне-
ний.
В результате выявляются группы конъюнкций, содержа-
щие по (n - 1) члену. С этой группой конъюнкций проводится та же
процедура, после которой получим группы конъюнкций, содержа-
щие по (n - 2) членов и так далее, пока не останется ни одного члена,
допускающего склеивания с каким либо другим членом.
Добавление к исходной ДНФ любого количества «склеенных»
членов не изменяет вида функции. Последующее исключение всех
членов, отмеченных в процессе склеивания, тоже не изменяет функ-

83
цию, так как они поглощаются склеенными членами. Все неотме-
ченные в процессе преобразований члены представляют собой про-
стые импликанты, а их дизъюнкция эквивалентна исходной функ-
ции.
Третий этап. Дизъюнкция всех простых импликантов может
оказаться избыточной формой представления функции. Поэтому
исследуется возможность удаления некоторых из них. Для этого
составляется импликантная таблица, строки которой обозначают-
ся выявленными на втором этапе простыми импликантами, а столб-
цы – элементарными конъюнкциями, входящими в совершенную
ДНФ.
Любая клетка этой таблицы отмечается, если простой импли-
кант, записанный в соответствующей строке, является составной
частью элементарной конъюнкции, записанной в соответствующем
столбце. Иначе говоря, данный простой импликант покрывает нашу
функцию на наборе, соответствующем элементарной конъюнкции,
записанной в столбце.
В каждом столбце при этом может оказаться несколько отме-
ченных клеток. Задача упрощения ДНФ сводится к вычеркиванию
из таблицы максимального количества строк таким образом, чтобы
заданная функция на всех наборах, обращающих ее в единицу, ока-
залась покрытой хотя бы одним простым импликантом.
Эту задачу можно выполнить в следующей последовательно-
сти:
1) выявляются столбцы, содержащие только одну помеченную
клетку. Простые импликанты, соответствующие этим клеткам, запи-
сываются в окончательное выражение для ДНФ как обязательные
члены. После этого в таблице вычеркиваются строки, соответст-
вующие обязательным простым ипликантам и столбцы, содержащие
отмеченные клетки в вычеркнутых строках. Вычеркивание столбцов
возможно потому, что соответствующие им элементарные конъ-
юнкции уже покрыты обязательными простыми импликантами и
поэтому их можно исключить из дальнейшего рассмотрения;
2) если после этого в таблице окажутся такие пары столбцов,
что всем отмеченным клеткам второго столбца соответствуют в тех
же строках отмеченные клетки первого столбца, а возможно, и неко-
торые другие отмеченные клетки, то первый столбец вычеркивается.
Это возможно потому, что какую бы совокупность простых импли-

84
кантов, покрывающую элементарную конъюнкцию, которая соот-
ветствует второму столбцу мы ни подобрали, этой совокупностью
автоматически будет покрываться и конъюнкция, соответствующая
первому столбцу;
3) строки, не содержащие после выполнения п.п. 1) и 2) ни од-
ной отмеченной клетки, также вычеркиваются. Это возможно пото-
му, что все конъюнкции, которые могут быть покрыты данным про-
стым импликантом, уже покрыты другими простыми импликантами,
которые должны войти в окончательное выражение для ДНФ;
4) в сокращенной таблице выявляется пара строк, содержащая
хотя бы по одной отмеченной клетке в каждом столбце. Простые
импликанты, соответствующие этим строкам, добавляются к ДНФ;
5). Если оказывается несколько вариантов выполнения п. 4) , то
все они сравниваются и выбирается простейший вариант.
Пример. Минимизировать функцию f (x
1
, x
2
, x
3
, x
4
) = x
1
x
2
x
4
٧
x
2
x
3
x
4
٧
⎯
x
1
⎯
x
2
x
3
٧
⎯
x
1
⎯
x
2
⎯
x
4
.
В результате развертывания элементар-
ных конъюнкций получим:
x
1
x
2
x
3
x
4,
x
1
x
2
⎯
x
3
x
4,
x
1
x
2
x
3
x
4,
⎯x
1
x
2
x
3
x
4,
⎯
x
1
⎯
x
2
x
3
x
4,
⎯
x
1
⎯
x
2
x
3
⎯
x
4,
⎯
x
1
⎯
x
2
x
3
⎯
x
4,
⎯
x
1
⎯
x
2
⎯
x
3
⎯
x
4.
После
приведения
подобных
слагаемых:
1) x
1
x
2
x
3
x
4,
2) x
1
x
2
⎯
x
3
x
4,
3)
⎯
x
1
x
2
x
3
x
4,
4)
⎯
x
1
⎯
x
2
x
3
x
4,
5)
⎯
x
1
⎯
x
2
x
3
⎯
x
4,
6)
⎯
x
1
⎯
x
2
⎯
x
3
⎯
x
4.
После
склеивания
получим:
1) x
1
x
2
x
4
(1,2),
2) x
2
x
3
x
4
(1,3),
3)
⎯x
1
x
З
x
4
(3,4),
4)
⎯x
1
⎯
x
2
x
3
(4,5),
5)
⎯x
1
⎯
x
2
⎯
x
4
(5,6).
Импликантная таблица представлена в таблице 3.7.
Таблица 3.7 - Импликантная таблица
x
1
x
2
x
3
x
4
x
1
x
2
⎯
x
3
x
4
⎯
x
1
x
2
x
3
x
4
⎯
x
1
⎯
x
2
x
3
x
4
⎯
x
1
⎯
x
2
x
3
⎯
x
4
⎯
x
1
⎯
x
2
⎯
x
3
⎯
x
4
x
1
x
2
x
4
X X
x
2
x
3
x
4
X
X
⎯
x
1
x
З
x
4
X X
⎯
x
1
⎯
x
2
x
3
X X
⎯
x
1
⎯
x
2
⎯
x
4
X X
85
Вычеркивая строки и столбцы, соответствующие обязательным
импликантам x
1
x
2
x
4
и
⎯
x
1
⎯
x
2
⎯
x
4
, получим упрощенную импликантную
таблицу (табл. 3.8).
Таблица 3.8 - Упрощенная импликантная таблица
⎯
x
1
x
2
x3x
4
⎯
x
1
⎯
x
2
x
3
x
4
x
2
x
3
x
4
X
⎯
x
1
x
З
x
4
X
X
⎯
x
1
⎯
x
2
x
3
X
Из упрощенной таблицы видно, что простой импликант x
1
x
З
x
4
покрывает обе оставшиеся конъюнкции. Теперь можно окончатель-
но записать минимальную ДНФ для функции f (x
1
, x
2
, x
3
, x
4
):
f (x
1
, x
2
, x
3
, x
4
) = x
1
x
2
x
4
٧
⎯
x
1
⎯
x
2
⎯
x
4
٧
⎯
x
1
x
З
x
4
.
Для уменьшения количества проверок на возможность склеи-
вания целесообразно все элементарные конъюнкции, содержащие
одинаковое число букв, сгруппировать по признаку одинакового
количества инвертированных (или не инвертированных) букв. Тогда
проверять можно только элементы двух соседних групп. Метод
Квайна с таким усовершенствованием называется методом Квайна-
Мак-Класки.
3.6
Автоматные
описания
При разработке системы управления некоторым объектом не-
обходимым этапом является формализация функционирования бу-
дущего устройства. Рассмотрим три вида описаний, относящихся к
типу автоматных.
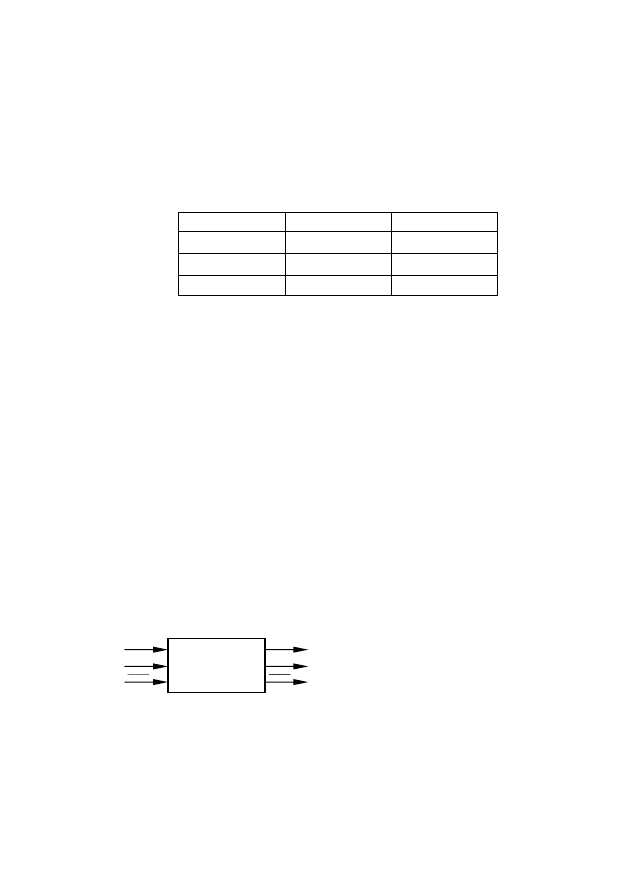
Будем представлять бу-
дущее устройство в виде
«черного ящика» (рис. 3.1), у
которого есть входы x
1
,
x
2
,...,x
q
и выходы y
1
, y
2
, ...,y
p
и «что-то внутри». Внутрен-
нее содержание «черного ящика» нам не известно, но его функцио-
нирование мы можем описывать с помощью внутренних состоя-
x
2
x
q
y
p
y
2
y
1
x
1
Рис. 3.1 – Модель черного ящика