Файл: Дискретная математика - учебное пособие.pdf

66 

1 – 2 – 3 – 6  1 – 3 – 2 – 4  1 – 3 – 5 – 6  1 – 4 – 5 – 2 

1 – 2 – 5 – 3  1 – 3 – 2 – 5  1 – 4 – 2 – 3  1 – 4 – 5 – 3 

1 – 2 – 5 – 4  1 – 3 – 4 – 2  1 – 4 – 2 – 5  1 – 4 – 5 – 6 

1 – 2 – 5 – 6  1 – 3 – 4 – 5  1 – 4 – 3 – 2 

Найдено  еще  пять  простых  цепей  (все  они  подчеркнуты).  Остальные 

18 цепей имеют продолжения: 

1 – 2 – 3 – 4 – 5 

1 – 3 – 2 – 4 – 5 

1 – 4 – 2 – 3 – 6 

1 – 2 – 3 – 5 – 4 

1 – 3 – 2 – 5 – 4 

1 – 4 – 2 – 5 – 3 

1 – 2 – 3 – 5 – 6 

1 – 3 – 2 – 5 – 6 

1 – 4 – 2 – 5 – 6 

1 – 2 – 5 – 3 – 4 

1 – 3 – 4 – 2 – 5 

1 – 4 – 3 – 2 – 5 

1 – 2 – 5 – 3 – 6 

1 – 3 – 4 – 5 – 2 

1 – 4 – 3 – 5 – 2 

1 – 2 – 5 – 4 – 3 

1 – 3 – 4 – 5 – 6 

1 – 4 – 3 – 5 – 6 

1 – 2 – 4 – 3 – 5 

1 – 3 – 5 – 2 – 4 

1 – 4 – 5 – 2 – 3 

1 – 2 – 4 – 3 – 6 

1 – 3 – 5 – 4 – 2 

1 – 4 – 5 – 3 – 2 

1 – 2 – 4 – 5 – 3 

1 – 4 – 2 – 3 – 5 

1 – 4 – 5 – 3 – 6 

1 – 2 – 4 – 5 – 6 

На  четвертом  этапе  получили  десять  простых  цепей.  На  пятом  (послед-

нем) получаем еще десять цепей. Они проходят через все вершины графа: 

1 – 2 – 3 – 4 – 5 – 6 

1 – 3 – 4 – 2 – 5 – 6 

1 – 2 – 5 – 4 – 3 – 6 

1 – 4 – 2 – 3 – 5 – 6 

1 – 2 – 4 – 3 – 5 – 6 

1 – 4 – 2 – 5 – 3 – 6 

1 – 2 – 4 – 5 – 3 – 6 

1 – 4 – 3 – 2 – 5 – 6 

1 – 3 – 2 – 4 – 5 – 6 

1 – 4 – 5 – 2 – 3 – 6 

Таким образом, всего в графе (рис. 3.9) имеется 26 простых цепей, соеди-

няющих вершины 1 и 6. Из них одна цепь содержит два ребра, 5 цепей содер-
жат по три ребра, 10 цепей – по четыре ребра и 10 цепей – по пять ребер. 

 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·   

Упражнения 

1.

  Сколько  простых  цепей,  соединяющих  вершины 1  и  6  и 

проходящих  через  вершину 2,  содержит  граф,  приведенный  на 
рисунке 3.9?  

2.

  На  основе  графа  (рис. 3.9)  построили  подграф,  удалив 

вершину 2.  Сколько  ребер  удалено?  Сколько  ребер  в  подграфе? 
Сколько простых цепей соединяют вершины 1 и 6 подграфа?  

3.

 Простой граф задан следующим образом: 

67 

G = {{1,2}, {1,4}, {1,5}, {2,3}, {2,4}, {3,4}, {3,5}, {4,5}}.  

а. Сколько в этом графе простых цепей, соединяющих вер-

шины 1 и 5?  

б. Сколько среди них простых цепей длины 1? 2? 3? 4?  

4.

 На какие вопросы Вы ответите «да»? 

а. Во всяком ли простом связном графе самая длинная про-

стая цепь проходит через все вершины графа? 

б. Дан связный граф. Всякий ли его надграф является связ-

ным? 

в. Верно ли, что в любом полном графе любые две его вер-

шины соединяет одинаковое число простых цепей? 

г.  Существует  ли  простой  связный  граф,  в  котором  каждые 

две вершины соединены точно двумя простыми цепями? 

д.  Всякий  ли  непустой  подграф  полного  графа  является 

полным? 

е. Всякий ли частичный граф полного графа является связ-

ным?  
 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·   

3.7 Двудольные графы 

Пусть  множество  V  вершин  простого  графа  G  состоит  из  двух  непу-

стых множеств V

1

 и V

2

, и пусть при этом выполняются условия: 

V = V

1 

∪

 V

2

;    V

1

∩

 V

2

 = 

∅

. 

Если рёбра графа G соединяют вершины разных множеств, и при этом 

нет ни одного ребра, соединяющего вершины одного и того же множества, то 
такой  граф  называется  двудольным.  Иными  словами:  граф  называется  дву-
дольным, если каждое ребро графа G соединяет некоторую вершину множе-
ства V

1

  c  какой-либо  вершиной  множества V

2

.  Пример  двудольного  графа 

приведен на рисунке 3.10. В этом графе  

V = {1, 2, 3, 4, 5, 6, 7},    V

1

 = {1, 2, 3},    V

2

 = {4, 5, 6, 7}. 

Рис. 3.10 

1

2

3

4

6

5

7

68 

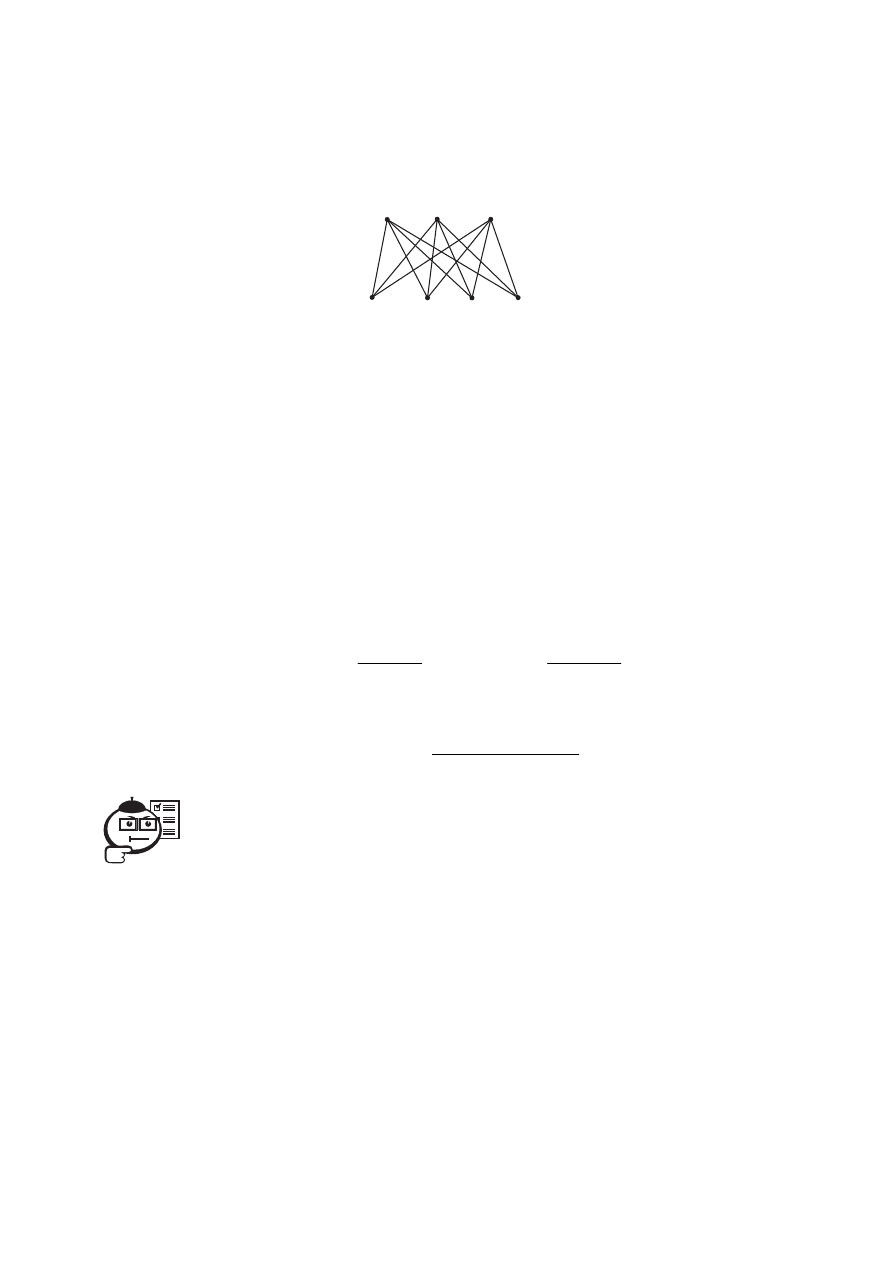
Двудольный  граф  называется  полным,  если  каждая  вершина 

множества V

1

 соединена с каждой вершиной множества V

2

 точно одним реб-

ром (рис. 3.11). 

Рис. 3.11 

Полный двудольный граф содержит K ребер, где 

K = |V

1

| · |V

2

|. 

Степень  любой  вершины  множества  V

1

  полного  двудольного  графа 

равна |V

2

|. Степень каждой вершины множества V

2

 равна |V

1

|. 

Дополнение  полного  двудольного  графа  есть  несвязный  граф,  состоя-

щий из двух компонент – полного графа G

1

 и полного графа G

2

. Обозначим: 

n = |V

1

|;    m = |V

2

|. 

Тогда  величины  K

1

  и  K

2

,  определяющие  число  ребер  компонент  G

1

  и 

G

2

, равны:  

;

2

)

1

(

2

1

−

=

=

n

n

C

K

n

.

2

)

1

(

2

2

−

=

=

m

m

C

K

m

Общее число K ребер дополнения полного двудольного графа равно: 

2

2

1

2

(

)

.

2

+

−

+

=

+

=

n

m

n

m

K

K

K

 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·   

Упражнения 

1.  Сколько  ребер  имеет  полный  двудольный  граф,  если 

|V

1

| = 4; |V

2

| = 7?  

2. Дано: в полном двудольном графе 143 ребра. Определите 

|V

1

| и |V

2

|, если 

|V

1

| > 1,  |V

2

| > 1,  |V

1

| > |V

2

|. 

3.  В полном  двудольном  графе  степень  каждой  вершины 

множества V

1

 равна 6, множества V

2

 – 8. Сколько ребер в графе?  

4. В некотором двудольном графе 

|V

1

| = 18,  |V

2

| = 10, 

а число ребер равно 18. Найдите число ребер дополнения до пол-
ного двудольного графа.  

1

2

3

4

6

5

7

69 

5. Известно, что в связном двудольном графе 

|V

1

| = 7,  |V

2

| = 10. 

Сколько  ребер  содержит  граф,  если  при  удалении  из  него 

любого ребра граф становится несвязным?  

6. Укажите вопросы, на которые Вы ответите «да». 
а. Может ли двудольный простой граф содержать петли? 
б. Верно ли, что нуль-граф, содержащий 7 вершин, является 

двудольным? 

в. Является ли двудольным граф, содержащий одну верши-

ну? 

г. Входит ли пустой граф в множество двудольных графов? 
д.  Может  ли  быть  двудольным  простой  граф,  содержащий 

35 ребер? 

е.  Может  ли  быть  связным  двудольный  граф,  если  в  нём 

12 рёбер и 

|V

1

| = 6,  |V

2

| = 7? 

ж.  Может  ли  быть  связным  двудольный  граф,  если  в  нём 

14 рёбер и  

V

1

| = 10,  |V

2

| = 6? 

з. Существуют ли связные двудольные графы, в которых все 

вершины  множества  V

1

  являются  четными,  а  все  вершины  мно-

жества V

2

 – нечетными?  

7. Укажите двудольные графы на рисунке 3.12. 

Рис. 3.12 

1

2

3

4

6

5

1

2

3

4

5

6

7

8

1

2

3

4

5

6

1

2

3

4

5

6

1

2

4

5

6

3

1

2

3

4

5

6

1

2

3

4

5

6

1

2

3

4

5

6

1

2

3

4

5

6

70 

8.  Укажите  номера  полных  двудольных  графов,  изображён-

ных на рисунке 3.12. 
 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·   

3.8 Двойственные графы 

Граф называется плоским, если на плоскости он изображён так, что его 

рёбра  пересекаются  только  в  вершинах.  Например,  граф,  изображённый  на 
рисунке 3.13,  является  плоским,  а  тот  же  граф  в  ином  изображении,  как  на 
рисунке 3.14, к плоским не относится, так как его ребра {1,3} и {2,4} пере-
секаются вне вершин. Граф называется планарным, если у него есть плоское 
изображение. Примером может служить граф на рисунке 3.14. Очевидно, что 
плоский граф одновременно является и планарным. 

Рис. 3.13 

Рис. 3.14 

Часть  плоскости,  ограниченная  со  всех  сторон  ребрами и  не  содержа-

щая  внутри  себя  ни  вершин,  ни  ребер,  называется  гранью.  Граф  на  рисун-
ке 3.13 имеет четыре грани: три внутренних – а, б, в – и одну внешнюю (бес-
конечную),  обозначенную  буквой г.  Бесконечную  грань  имеет  любой 
плоский граф. Петля также образует грань. Например, на рисунке 3.15 грани 
а и б образованы петлями. 

Рис. 3.15 

Если  параллельно  какому-либо  ребру  графа  провести  одно  ребро,  то 

получим новую грань. Например, на рисунке 3.15 вершины 2 и 3 соединены 

1

2

3

4

а

б

в

г

1

2

3

4

1

2

3

а б

в

г д е