ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16662
Скачиваний: 202

61
4) семь нечетных вершин и шесть ребер?
5) семь вершин и степень каждой вершины равна 2?
6) шесть вершин и семь ребер?
7) восемь вершин и степень каждой из них равна 3?
3.
Сколько ребер в полном графе, содержащем 10 вершин?
4.
В полном графе 105 ребер. Сколько в нём вершин?
5.
В частичном графе полного графа, содержится 12 вершин и
54 ребра. Сколько ребер в дополнении частичного графа?
6.
Из полного графа, содержащего 20 вершин, удалили не-
сколько вершин. В получившемся подграфе оказалось 66 ребер.
а. Сколько вершин удалено?
б. Сколько ребер удалено?
7.
Найдите степень вершины полного графа, имеющего
91 ребро.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
3.4 Маршруты, цепи, циклы
Эти понятия интуитивно ясны. Однако авторы публикаций по теории
графов обычно стремятся дать им точные определения. Например, Ф. Харари
пишет: «Маршрутом в графе G называется чередующаяся последовательность
вершин и рёбер v
0
, x
1
, v
1
, …, v
n – 1
, x
n
, v
n
; эта последовательность начинается и
кончается вершиной, и каждое ребро последовательности инцидентно двум
вершинам, одна из которых непосредственно предшествует ему, а другая непо-
средственно следует за ним» [52, с. 26]. В этом определении буквой v с цифро-
вым индексом Ф. Харари обозначает вершины графа, а буквой x – рёбра.
Согласно определению, данному Ф. Харари, всякий маршрут начинается
с номера вершины и оканчивается номером вершины. В соответствии с этим
если в графе нет кратных рёбер и петель, то в маршруте рёбра можно не назы-
вать, достаточно перечислить только номера вершин. Такое представление
маршрутов называется вершинным. Примером маршрута в графе (рис. 3.1) яв-
ляется последовательность вершин вида 1 – 2 – 4 – 3 – 5 – 2 – 4 – 6.
Маршрут называется цепью, если в нем нет повторяющихся ребер. Всякая
цепь имеет начальную вершину и конечную [33, с. 165]. (О. Е. Акимов исполь-
зует другую терминологию: «Цепь имеет голову и хвост» [1, с. 238]). Цепь
называется простой, если при вершинном её представлении в ней нет повторя-
ющихся вершин. Пример простой цепи (рис. 3.1): 2 – 4 – 3 – 5.

62
Маршруты, цепи и простые цепи могут быть замкнутыми и разомкну-
тыми. В замкнутых маршрутах (а также цепях и простых цепях) начальная и
конечная вершины совпадают, в разомкнутых – не совпадают. Примером за-
мкнутого маршрута является последовательность вершин (рис. 3.1): 1 – 2 – 4 –
– 3 – 5 – 2 – 4 – 6 – 1. Замкнутая цепь называется циклом. Простая замкнутая
цепь называется простым циклом. Пример простого цикла: 2 – 4 – 3 – 5 – 2
(рис. 3.1).
Понятие простого цикла в теории графов является одним из важнейших.
В литературе можно встретить различные его определения, но по смысловому
содержанию они в основном совпадают. Например:
«Простым циклом в графе называется цикл, не проходящий ни через одну
из вершин графа более одного раза» [2, с. 17].
«Если в некоторой цепи начальная и конечная вершины совпадают, то та-
кая цепь называется циклом» [40, с. 55].
«Цепь, в которой все вершины различны, кроме, может быть, её концов,
называется простой. Замкнутая простая цепь называется простым циклом» [38,
с. 196].
Этим определениям не противоречит и такой цикл, в котором только одно
ребро, например 1 – 2 – 1 (рис. 3.1), а также граф, состоящий из одной вершины
с петлей, так как формально эта петля образует цикл. Однако при таких допу-
щениях получается, что во всяком графе, содержащем хотя бы одно ребро, со-
держится не менее одного цикла. В некоторых случаях это может создать зна-
чительные трудности, например в определении графа типа «дерево». Поэтому
будем считать, что во всяком цикле содержится не менее трёх вершин, и такие
последовательности, как 1 – 2 – 1 циклами не являются.
Число ребер, входящих в цепь, называется длиной цепи или расстоянием
между начальной и конечной вершинами. Например, цепь 1, 2, 4, 3, 5 (рис. 3.1)
содержит четыре ребра, следовательно, расстояние между вершинами 1 и 5, а
также длина цепи равны 4.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Укажите длины (рис. 3.1): самой короткой и самой длинной
из простых цепей, ведущих от вершины 1 к вершине 6.
2.
В нижеприведенном списке укажите простые циклы
(рис. 3.1).
1) 1, 2, 5, 6;
2) 1, 2, 4, 6, 1;
3) 2, 4, 3, 5, 2;

63
4) 2, 1, 6, 4, 2;
5) 1, 3, 2, 4, 1;
6) 1, 2, 4, 3, 5, 2.
3.
Укажите вопросы, на которые Вы ответите «да».
а. Может ли последовательность, обозначающая маршрут,
начинаться с номера ребра и оканчиваться номером вершины?
б. Может ли цепь состоять из одного ребра (и двух вершин)?
в. Может ли простой граф содержать цикл, состоящий из од-
ного ребра?
г. Существуют ли маршруты в нуль-графе, множество вершин
которого не является синглетоном?
д. Верно ли, что если простой граф содержит точно одну вер-
шину и не является нуль-графом, то он содержит цикл?
е. Верно ли, что если простой граф состоит из двух вершин и
не является нуль-графом, то в нем нет циклов?
ж. Могут ли в цикле повторяться вершины кроме первой и
последней?
з. Верно ли, что если в простом графе нет циклов, то в нем ре-
бер столько же, сколько и вершин?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
3.5 Связность графа
Две вершины v и w графа G называются связными, если они соединены
хотя бы одной простой цепью. Если же в графе нет ни одной цепи, соединяю-
щей вершины v и w, то эти вершины называются несвязными. Например, вер-
шины 1 и 6 (рис. 3.7) соединяет цепь 1, 7, 2, 6, следовательно, они являются
связными. Пара вершин 2 и 3 к связным не относятся, так как ни одна цепь их
не соединяет. Если в графе каждые две вершины связны, то такой граф называ-
ется связным. Если же граф содержит хотя бы одну пару несвязных вершин, то
граф называется несвязным.
Рис. 3.7
1
2
3
4
5
6
7
8
64
Согласно этим определениям, граф, изображенный на рисунке 3.9, явля-
ется связным, а графы, приведенные на рисунках 3.7 и 3.8, – несвязными.
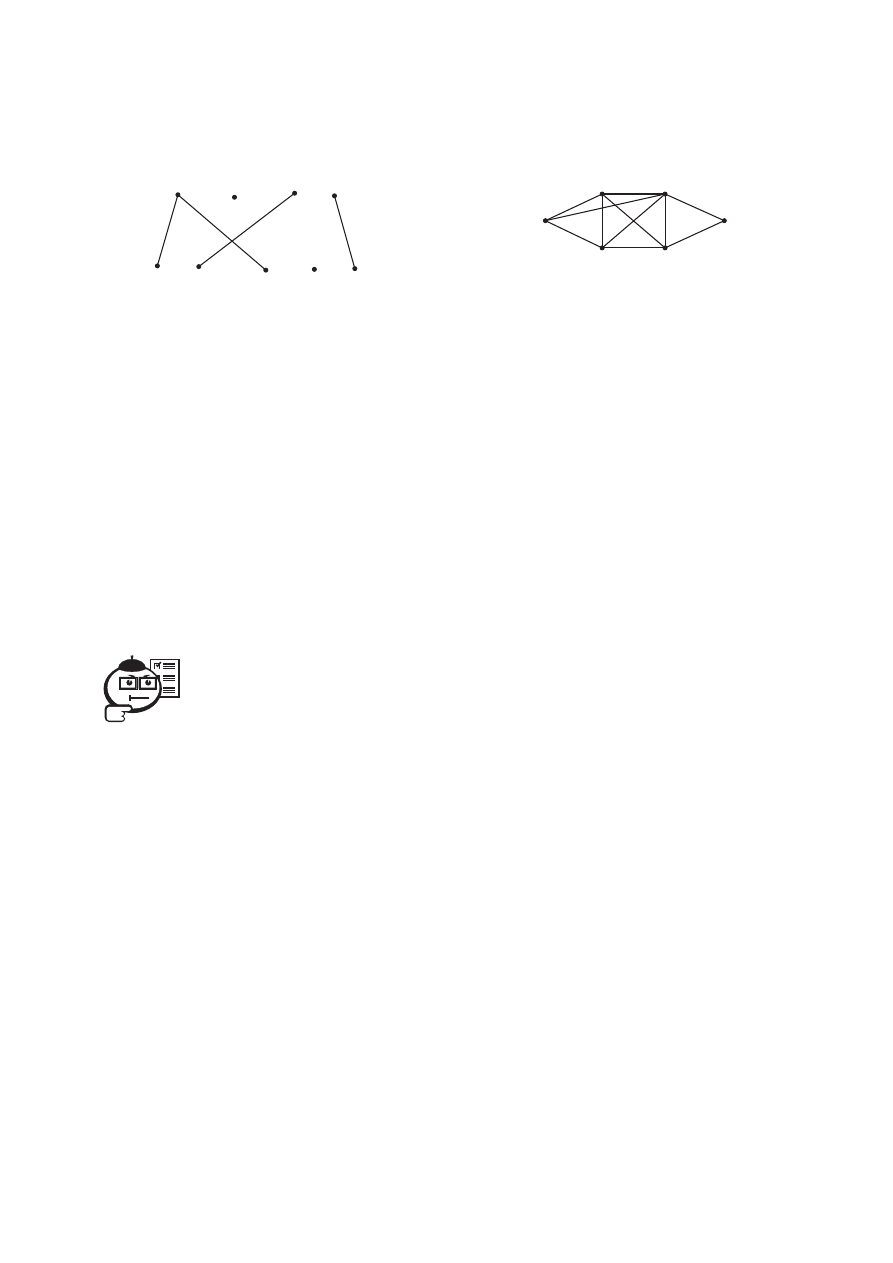
Рис. 3.8
Рис. 3.9
Граф, приведённый на рисунке 3.7, состоит из двух компонент, где каж-
дая компонента представляет собой связный граф. В графе (рис. 3.8) содержит-
ся 5 компонент.
(Необходимо заметить, что согласно нормам современного русского язы-
ка слово компонент относится к категории мужского рода [3]. Однако в мате-
матической литературе используется форма женского рода [47, с. 28; 14, с. 249;
33, с. 173; 8, с. 102; 51, с. 60].)
Число компонент, из которых состоит граф, называется степенью связно-
сти. Граф, изображённый на рисунке 3.7, имеет степень связности, равную 2.
Степень связности графа, приведенного на рисунке 3.8, равна 5.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Укажите степень связности графа:
G = {{1,6}, {2,7}, {3,5}, {3,8}, {4,8}, {5,8}}.
2.
Укажите степень связности дополнения графа:
G = {{1,2}, {1,4}, {1,5}, {1,6}, {2,3}, {2,5}, {2,6},
{3,4}, {3,5}, {3,6}, {4,5}, {4,6}}.
3.
На какие вопросы из следующих Вы дадите утвердитель-
ные ответы?
а. Может ли нуль-граф быть однокомпонентным?
б. Может ли простой граф быть однокомпонентным, если
в нем 10 вершин и 8 ребер?
в. Верно ли, что простой граф на n вершинах, не содержащий
ни одного ребра, имеет степень связности, равную n?
г. Из связного графа, в котором нет циклов, удалили одно
ребро. Будет ли получившийся граф двухкомпонентным?
1
2
3
4
5
6
8
5
8
1
2
3
4
6
5

65
д. Может ли простой граф быть связным, если в нем 6 вершин
и 5 ребер?
е. Может ли простой граф, содержащий n вершин и n ребер,
иметь степень связности, равную n?
ж. Может ли граф быть связным, если он содержит восемь
вершин и четыре ребра?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
3.6 Нахождение простых цепей в простом графе
Пусть задан простой граф. Выберем в нем какие-либо две вершины v и w.
Задача состоит в том, чтобы найти все простые цепи, соединяющие эти верши-
ны. Очевидно, что задача разрешима, если граф является связным. В случае не-
связных графов задача также разрешима, но при этом возможны два варианта:
а)
вершины v и w относятся к одной и той же компоненте. Очевидно, что
все простые цепи будут проходить через вершины только этой компо-
ненты;
б)
вершины v и w входят в различные компоненты графа. В этом случае
число простых цепей равно нулю.
Метод нахождения всех простых цепей (он является модификацией мето-
да отыскания кратчайших путей [2]) рассмотрим на примере связного графа,
приведенного на рисунке 3.9.
Допустим, что начальной является вершина 1, конечной – вершина 6. На
первом этапе выясним, сколько существует способов выйти из первой верши-
ны. Так как ее степень равна 3, то имеем три варианта: 1 – 2, 1 – 3, 1 – 4.
Из вершины 2 можно выйти в трех направлениях: к вершинам 3, 4, 5 (в
вершину 1 не возвращаемся). Из вершины 3 движение возможно четырьмя
способами, из вершины 4 – тремя. Таким образом, на втором этапе получа-
ем:
1 – 2 – 3
1 – 3 – 2
1 – 4 – 2
1 – 2 – 5
1 – 3 – 4
1 – 4 – 3
1 – 2 – 4
1 – 3 – 5
1 – 4 – 5
1 – 3 – 6
Заметим, что одну простую цепь мы уже нашли (подчеркнута): 1 – 3 – 6.
Остальные цепи имеют продолжение:
1 – 2 – 3 – 4 1 – 2 – 4 – 3 1 – 3 – 5 – 2 1 – 4 – 3 – 5
1 – 2 – 3 – 5 1 – 2 – 4 – 5 1 – 3 – 5 – 4 1 – 4 – 3 – 6