ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16667
Скачиваний: 202
71
тремя кратными рёбрами. Ограниченные ими участки плоскости дают гра-
ни г и д.
Двойственным по отношению к связному плоскому графу G называет-
ся граф G
*
, построенный следующим образом:
1) в каждой грани заданного плоского графа ставится вершина
графа G
*
;
2) если какая-либо вершина графа G
*
отделена точно одним ребром
графа G от другой вершины графа G
*
, то эти вершины соединяются
ребром, относящимся к графу G
*
.
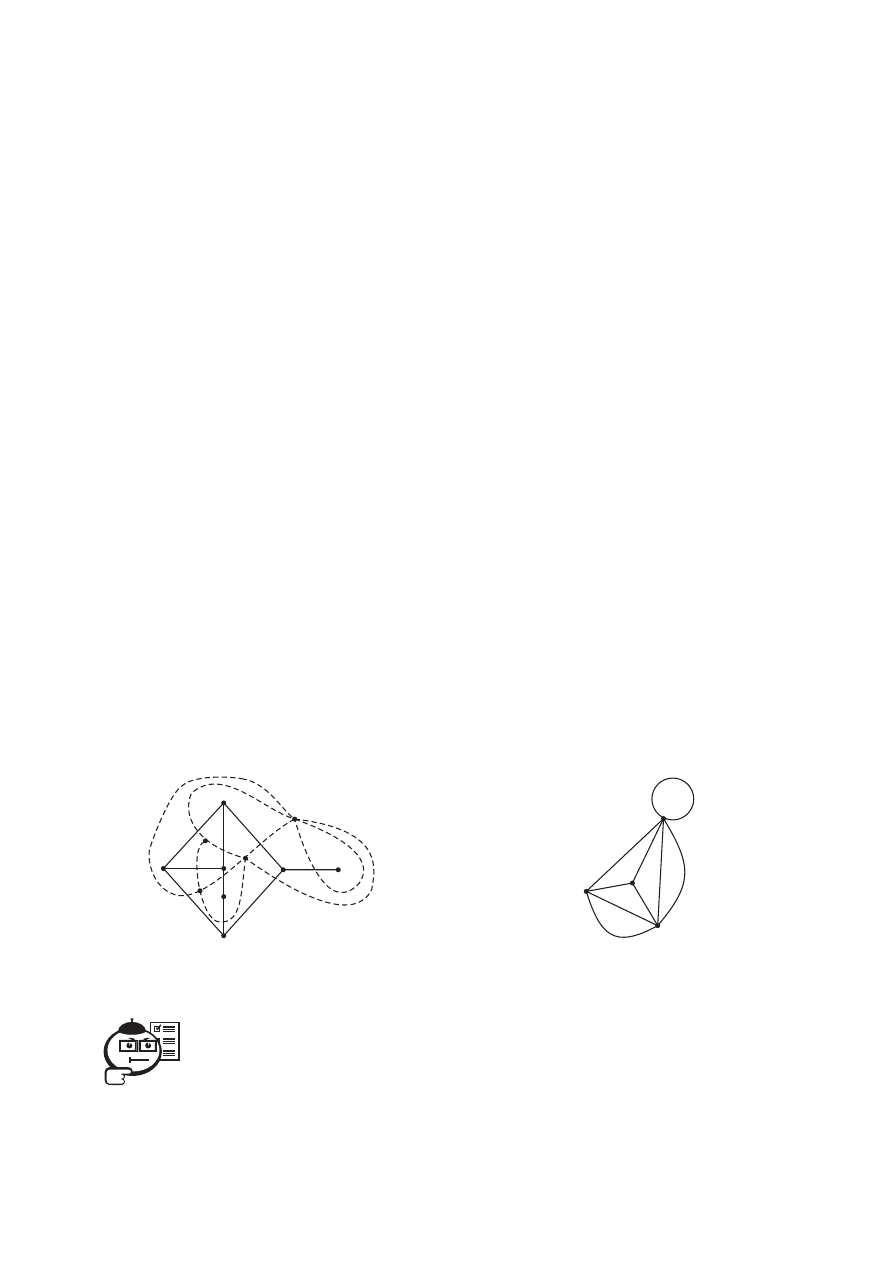
Поясним это на примере. Пусть дан граф (рис. 3.16), содержащий че-
тыре грани (из них одна – бесконечная). В каждой грани поставим по одной
вершине графа G
*
. Обозначим их буквами a, b, c, d. Находим ребра графа G
*
.
Вершина 5 является висячей. Ребру {4,5} в графе G
*
соответствует петля.
Вершина а отделена от вершины d ребром {1,2}. Проводим ребро {a, d} (на
рис. 3.16 оно обозначено пунктиром). Вершина b отделена от вершины d
ребром {2,4}, соединяем вершины b и d ребром {b, d
} и т. д.
На рисунке 3.17 изображен граф, двойственный по отношению к графу,
приведённому на рисунке 3.16. Пусть n, r, q – число вершин, ребер и граней
графа G соответственно; n
*
,
r
*
, q
*
– число вершин, ребер и граней графа G
*
.
Тогда очевидно, что справедливы следующие зависимости между числами n,
r, q и n
*
,
r
*
, q
*
:
n
*
= q, r
*
= r, q
*
= n.
Рис. 3.16
Рис. 3.17
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Для графа, приведенного на рисунке 3.17, укажите,
сколько вершин, ребер и граней имеет его двойственный граф?
a
b
c
d
1
2
3
4
5
6
7
a
b
c
d
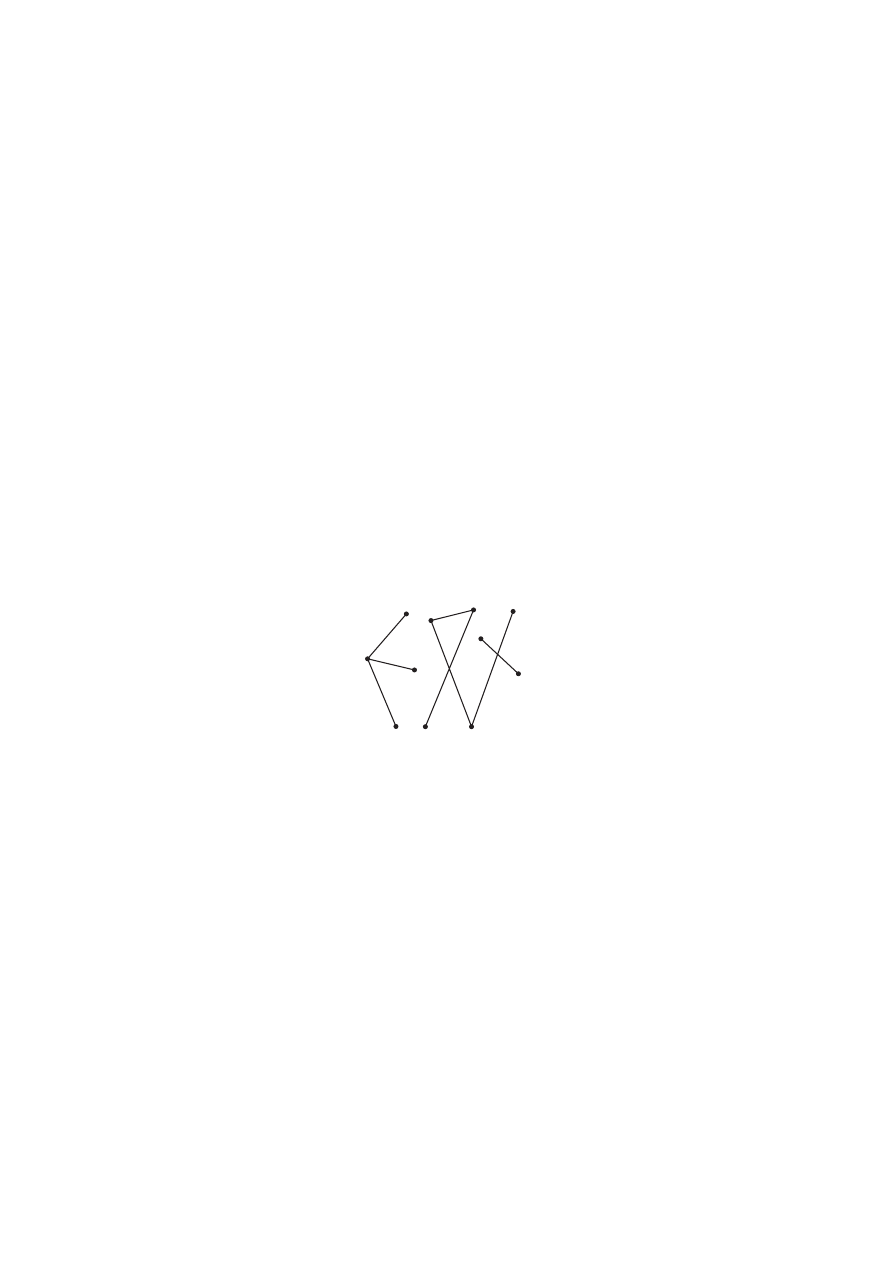
72
2. Сколько вершин, ребер и граней имеет граф, двойствен-
ный графу, приведенному на рисунке 3.13?
3. Укажите номера графов, являющихся планарными
(рис. 3.12).
4.
Укажите номера графов, являющихся плоскими
(рис. 3.12).
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
3.9 Древовидные графы
Термин «дерево» для особой разновидности графов ввел в 1857 г. ан-
глийский математик Артур Кэли (1821–1895), с 1870 г. иностранный член-
корреспондент Петербургской академии наук.
Деревом называется связный граф, не содержащий циклов. Несвязный
граф, не содержащий циклов, называется лесом. На рисунке 3.18 приведен
трехкомпонентный лес. Первую компоненту этого леса образует дерево с
вершинами 1,2,3,4, вторую – 5,6,7,8,9, третью – 10,11.
Рис. 3.18
Приведем без доказательств четыре теоремы о деревьях.
Теорема 1. Всякое дерево содержит n – 1 ребер, где n – число вершин.
Теорема 2. Всякий лес содержит n – k ребер, где k – число компонент
связности;
Теорема 3. Любые две вершины дерева соединены точно одной про-
стой цепью.
Теорема 4. Если в дереве любые две вершины соединить ребром, то в
графе появится один цикл.
Доказательства теорем можно найти в [33; 47].
Если связный граф содержит цикл, то после удаления любого ребра,
входящего в цикл, этот цикл разрушается, но связность графа сохраняется.
Применим операцию разрушения циклов к каждому циклу графа. Тогда в
1
2
3
4
5
6
7
8
9
10
11
73
графе не останется циклов и получится связный частичный граф, являющий-
ся деревом. Полученное дерево называется óстовом. Значит, остов – это
связный частичный граф данного связного графа G, содержащий все верши-
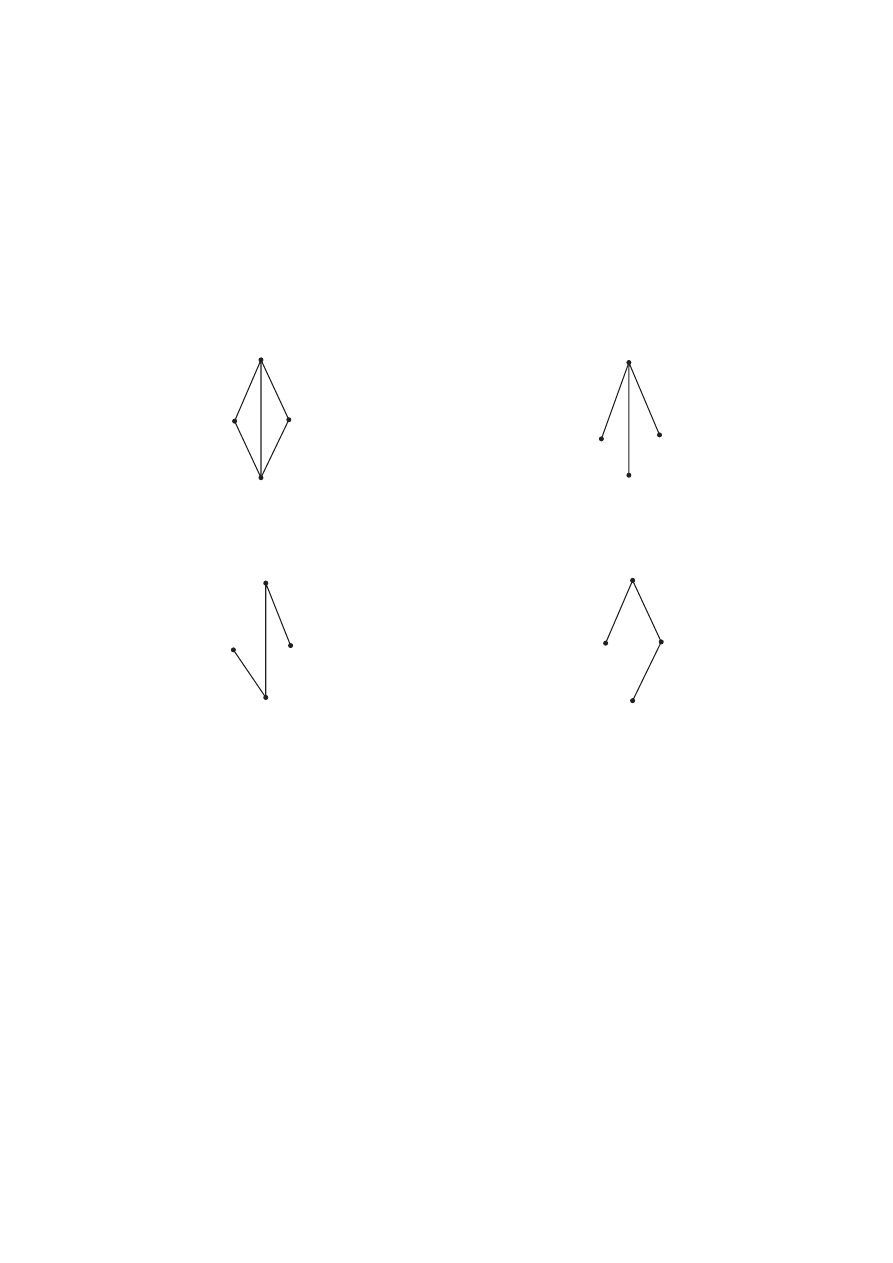
ны графа G, но не содержащий циклов. Рассмотрим, например, граф, изоб-
раженный на рисунке 3.19. Удалим из него ребра {1,4} и {3,4}. Получим
остов (рис. 3.20). Если из графа (рис. 3.19) удалить ребра {1,2} и {3,4}, то
получим другой остов (рис. 3.21), если удалить рёбра {1,4} и {2,4}, то полу-
чим ещё один остов (рис. 3.22), и т. д.
Рис. 3.19
Рис. 3.20
Рис. 3.21
Рис. 3.22
Наименьшее число z, показывающее, сколько ребер необходимо уда-
лить из графа, чтобы получить его остов, называется цикломатическим чис-
лом. Если n – число вершин, m – число ребер, k – число компонент, то
z = m – n + k,
т. е. чтобы найти цикломатическое число произвольного графа, необходимо
из числа ребер вычесть число вершин и к результату прибавить число ком-
понент.
В случае связного графа k = 1, следовательно,
z = m – n + 1.
Например, для графа, приведенного на рисунке 3.19, значения m, n и z
равны:
m = 5; n = 4; z = 5 – 4 + 1 = 2.
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4

74
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Найдите цикломатическое число графа, изображенного
на рисунке 3.18.
2. В связном графе 18 вершин. Сколько ребер содержит его
остов?
3. В нуль-графе 38 вершин. Каково наименьшее число ре-
бер, которые необходимо в него ввести, чтобы получить связный
граф?
4. В дерево из 25 вершин ввели 4 ребра. Сколько ребер в
новом графе?
5. В связном графе 20 вершин и 40 ребер. Сколько ребер
необходимо удалить, чтобы получить остов?
6. Сколько ребер необходимо удалить из дерева, содержа-
щего 20 ребер, чтобы получился лес из 15 деревьев?
7. Укажите номера вопросов, на которые Вы ответите «да».
Верно ли, что
1) цикломатическое число дерева равно нулю?
2) всякое дерево является планарным графом?
3) число z полного графа на n вершинах можно найти по
формуле
?
2
2
3
2
+
−
=
n
n
z
4) формула для цикломатического числа справедлива для
непланарных графов?
5) формула для нахождения цикломатического числа спра-
ведлива и для псевдографов?
6) одновершинный граф с одной петлей является деревом?
7) изолированная вершина может быть компонентой леса?
8) граф, в котором число ребер равно числу вершин, может
быть деревом?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
3.10 О прикладных аспектах теории графов
Теории графов в современной дискретной математике уделяется очень
большое внимание. Её теоретические и прикладные вопросы рассматриваются

75
не только в публикациях, посвященных графам [47; 52], но и во многих (если не
в большинстве) учебных пособиях по дискретной математике, например [1; 8;
14; 28; 32; 33; 35; 38; 40; 51; 57]. С их помощью решаются следующие задачи:
а) нахождение инверсных контактных структур;
б) представление контактных структур в виде сети электронных логиче-
ских элементов.
Вообще же необходимо отметить, что, как уже отмечалось в начале дан-
ного раздела, теория графов отличается очень большими возможностями по её
применению в различных областях науки, особенно в многочисленных разде-
лах дискретной математики, где благодаря графам обеспечивается высокая сте-
пень наглядности в процессе решения многих задач из области дискретных
структур.
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 3.1
· · · · · · · · · · · · · · · · · · · · · · ·
1. Задача о раскраске географических карт. Эта задача известна в литера-
туре под названием проблемы (гипотезы) четырёх красок [14; 35; 47; 52]. В [52]
она формулируется следующим образом: «Раскраской плоской карты G назы-
вается такое приписывание цветов областям в G, что никакие две смежные об-
ласти не получают одинакового цвета» [52, с. 156]. Почти так же формулирует-
ся она в терминах теории графов: «Раскраской графа называется такое
приписывание цветов его вершинам, что никакие две смежные вершины не по-
лучают одинакового цвета» [52, с. 152].
2. С развитием цифровой техники возникла проблема печатного монтажа.
В её решении нашла применение теорема (критерий) Понтрягина – Куратовско-
го [14; 52; 57], позволяющая определить, существует ли возможность выпол-
нить печатный монтаж только на одной стороне печатной платы.
3. В [28, с. 186] перечислены задачи, которые решаются на основе алго-
ритма нахождения максимального потока в графовой модели: транспортная за-
дача (о перевозе с минимальными затратами каких-либо грузов); задача о спро-
се и предложении (о стратегии, при которой торговец получит максимальную
прибыль); задача о кратчайшем пути (о поиске пути с минимальной стоимо-
стью проезда); задача об оптимальном использовании дорог; задачи о складе,
об оптимальном назначении, о поставщике и многие другие.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·