ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16681
Скачиваний: 202

106
3) выполните операции второго этапа метода Квайна. Опреде-
лите число неподчёркнутых конъюнкций трёх аргументов и число
неповторяющихся конъюнкций, содержащих по два аргумента;
4) найдите число простых импликант и число вхождений ар-
гументов сокращенной формы функции.
2.
Определите число простых импликант и число вхождений
аргументов сокращенных форм функций:
1)
;
)
,
,
(
BC
C
A
AC
AB
C
B
A
f
+
+
+
=
2)
);
7
,
4
,
3
,
2
,
1
(
)
,
,
(
=
C
B
A
f
3)
;
)
7
,
6
,
5
,
4
,
3
,
0
(
)
,
,
,
(
=
D
C
B
A
f
4)
)
15
,
14
,
11
,
10
,
7
,
6
,
2
(
)
,
,
,
(
=
D
C
B
A
f
;
5)
)
15
,
14
,
13
,
11
,
10
,
7
,
3
,
2
,
1
,
0
(
)
,
,
,
(
=
D
C
B
A
f
.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
5.3 Метод Петрика
Сокращённая форма многих функций не является минимальной. В вопро-
сах нахождения минимальных форм полную ясность ввёл Петрик [14, c. 106],
разработав свой метод нахождения всех возможных минимальных форм на ос-
нове сокращённых [12].
Метод Петрика поясним на примере функции, СДНФ которой имеет вид:
.)
15
,
14
,
12
,
11
,
9
,
8
,
7
,
6
,
5
,
4
,
2
,
0
(
=
f
(5.2)
Представим её в сокращённой форме:
.
f
C D
A D
AB
BD
BC
AB C
ABD
ACD
=
+
+
+
+
+
+
+
(5.3)
Это выражение не является минимальным. Оно содержит лишние про-
стые импликанты. Если их удалить, то функция не изменится. Удалим из выра-
жения (5.3) простую импликанту, например
,
C
B
A
и получившееся выражение
представим в СДНФ – функция останется той же самой. Но если удалить им-
пликанту
A D
и найти СДНФ, то она не совпадёт с (5.2), т. е. функция изменит-
ся.
В принципе таким способом можно получить все варианты тупиковых
форм
, т. е. таких выражений, в которых не найдётся ни одной простой импли-
канты, которую можно было бы удалить. Подобный метод хотя и возможен, но
вследствие его громоздкости с практической точки зрения интереса не пред-
ставляет. Метод Петрика позволяет найти все тупиковые формы гораздо быст-

107
рее. Основу его составляет импликантная матрица (табл. 5.1), в которой стро-
ки озаглавлены простыми импликантами, а колонки – минтермами.
Таблица 5.1
0 2 4 5 6 7 8 9 11 12 14 15
CD
1 1
1
1
A D
1 1 1 1
AB
1 1 1 1
BD
1 1
1 1
BC
1 1
1 1
AB C
1 1
ABD
1 1
ACD
1
1
Основное поле заполняем единицами по следующему правилу: берём ка-
кую-либо простую импликанту и выясняем, из каких минтермов она состоит.
Эти минтермы отмечаем единицами. В первой строке в левой колонке записана
простая импликанта
.
D
C
Она получена склеиванием минтермов 0, 4, 8, 12. Эти
минтермы отмечаем в таблице: в колонках 0, 4, 8, 12 ставим единицы.
Переходим ко второй строке. В ней записана простая импликанта
.
D
A
Она получается склеиванием минтермов 0, 2, 4, 6. В колонках с номерами 0, 2,
4, 6 также ставим единицы. Аналогичным образом заполняем все строки табли-
цы.
В колонках находится различное число единиц. Например, в колонке 2
записана одна единица. Она говорит о том, что минтерм m
2
останется в функ-
ции, если импликанта
D
A
не будет удалена. Следовательно, её удалять нельзя.
Также нельзя удалять и импликанту
.
B
A
Обе они войдут во все формы функ-
ции. Но из импликантной матрицы их и соответствующие им минтермы следу-
ет удалить. В таблице 5.1 эти минтермы отмечены птичками (под колонками).
После всех удалений получим упрощённую матрицу (табл. 5.2).
Введём логические переменные ϕ
1
, ϕ
2
, …, ϕ
6
(они записаны в левой ко-
лонке табл. 5.2) со следующей интерпретацией: ϕ
1
= 1, если конъюнкция
D
C

108
входит в функцию, и ϕ
1
= 0, если не входит; ϕ
2
= 1, если простая импликанта
D
B
входит в функцию, и ϕ
2
= 0 в противоположном случае, и т. д. до послед-
ней простой импликанты.
Таблица 5.2
8 9 11 12 14 15
ϕ
1
CD
1
1
ϕ
2
BD
1 1
ϕ
3
BC
1 1
ϕ
4
AB C
1 1
ϕ
5
ABD
1 1
ϕ
6
ACD
1
1
Тогда если ϕ
1
+ ϕ
4
= 1, то минтерм m
8
входит в функцию. Если ϕ
4
+ ϕ
5
= 1,
то m
9
входит в функцию, и т. д.
Условие, при котором все минтермы останутся в функции, запишется в
виде следующего уравнения:
(ϕ
1
+ ϕ
4
) (ϕ
4
+ ϕ
5
) (ϕ
5
+ ϕ
6
) (ϕ
1
+ ϕ
2
) (ϕ
2
+ ϕ
3
) (ϕ
3
+ ϕ
6
) = 1.
Раскроем скобки и выполним все операции согласно теореме поглоще-
ния:
ϕ
2
ϕ
4
ϕ
6
+ ϕ
2
ϕ
3
ϕ
4
ϕ
5
+ ϕ
1
ϕ
2
ϕ
5
ϕ
6
+ ϕ
1
ϕ
3
ϕ
4
ϕ
6
+ ϕ
1
ϕ
3
ϕ
5
= 1.
Расшифруем решение. Каждая конъюнкция в полученном уравнении мо-
жет быть равной единице. Берём первую конъюнкцию. Если
ϕ
2
ϕ
4
ϕ
6
= 1,
то это значит, что согласно таблице 5.2 в функцию входят простые импликанты
,
D
B
C
B
A
и ACD. Добавим к ним обязательные простые импликанты B
A
и
.
D
A
Получим первый вариант искомой тупиковой формы:
,
1
ACD
C
B
A
D
B
B
A
D
A
f
+
+
+
+
=
содержащей 12 вхождений аргументов.
Аналогично находим ещё четыре тупиковые формы:
2
;
f
A D
AB
BD
BC
AB C
ABD
=
+
+
+
+
+
;
3
ACD
D
B
A
D
B
D
C
B
A
D
A
f
+
+
+
+
+
=

109
;
4
ACD
C
B
A
BC
D
C
B
A
D
A
f
+
+
+
+
+
=
.
5
D
B
A
BC
D
C
B
A
D
A
f
+
+
+
+
=
Таким образом, функция (5.2) имеет пять тупиковых дизъюнктивных
нормальных форм, среди которых одна минимальная. В ней 11 вхождений ар-
гументов.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Сколько тупиковых форм имеют следующие функции, за-
висящие от четырёх переменных? Сколько вхождений аргументов в
минимальной форме?
1)
;
)
15
,
13
,
12
,
10
,
8
,
7
,
6
,
2
(
=
f
2)
;
)
15
,
14
,
10
,
9
,
7
,
5
,
4
,
2
,
0
(
=
f
3)
;
)
11
,
10
,
9
,
8
,
5
,
4
,
1
(
=
f
4)
;
)
15
,
14
,
12
,
9
,
8
,
7
,
6
,
5
(
=
f
5)
;
)
15
,
14
,
13
,
12
,
11
,
9
,
8
,
7
,
6
,
4
,
0
(
=
f
6)
.)
15
,
14
,
13
,
12
,
11
,
10
,
8
,
7
,
6
,
3
,
0
(
=
f
2.
Сколько простых импликант и сколько вхождений аргу-
ментов в минимальных ДНФ, если все функции зависят от четырёх
переменных?
1)
(0, 3, 5, 6, 9, 15);
=
f
2)
(1, 2, 12, 13, 14, 15);
=
f
3)
(1, 2, 7, 10, 12, 15);
=
f
4)
(1, 2, 3, 5, 6, 7, 9,13);
=
f
5)
.)
15
,
14
,
13
,
12
,
11
,
10
,
8
,
7
,
6
,
3
,
2
,
1
,
0
(
=
f
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
5.4 Карты Вейча
При помощи карт Вейча легко осуществляются различные преобразова-
ния булевых формул: минимизация, нахождение СДНФ и СКНФ, инвертирова-
ние, дифференцирование и др.
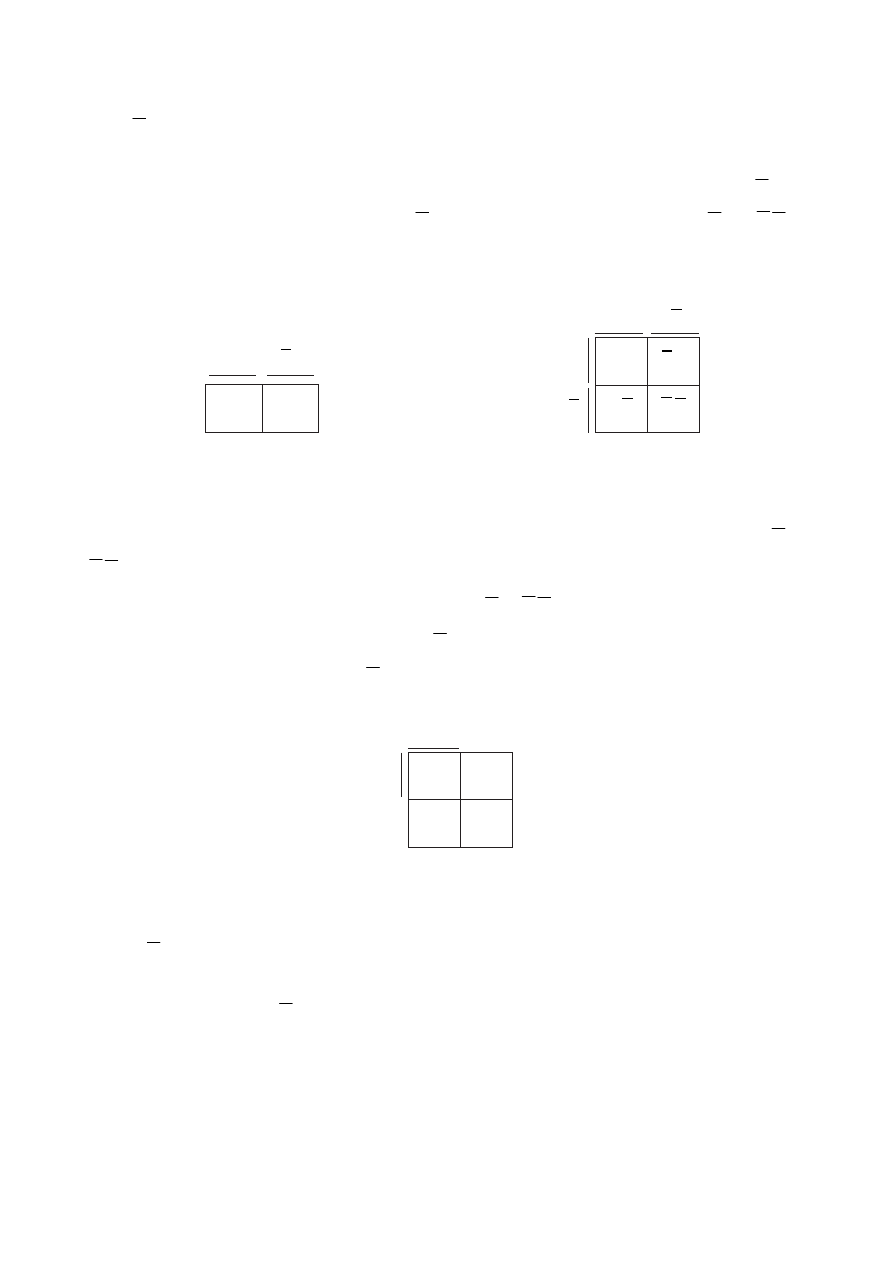
Простейшей является карта одной переменной (рис. 5.1). Но она не имеет
никакого значения, ни прикладного, ни теоретического. Поэтому изучение карт
начнём с двух переменных (рис. 5.2). Левая половина карты обозначена бук-
вой A, правая – той же буквой, но с инверсией. По горизонтали карта также
110
разделена на две части. Верхняя половина обозначена буквой B, нижняя – бук-
вой
.
B
В результате карта оказалась разделённой на четыре клетки. Левая
верхняя клетка находится на пересечении областей A и B – записываем в неё
минтерм AB. Правая верхняя клетка находится на пересечении областей A и B.
Записываем в эту клетку минтерм
.
B
A
Аналогично записываем B
A
и
B
A
в
оставшихся двух клетках.
Рис. 5.1
Рис. 5.2
На рисунке 5.3 приведена та же карта, но в трёх клетках её поставлены
единицы. Эти единицы говорят о том, что дизъюнкция минтермов AB, B
A
и
B
A
образуют некоторую функцию:
,
)
,
(
B
A
B
A
AB
B
A
f
+
+
=
а в клетке, относящейся к минтерму
,
B
A
единицы нет (что обозначает: в ней
стоит нуль), поэтому минтерм B
A
в запись функции
)
,
( B
A
f
не включён.
Рис. 5.3
На рисунке 5.3 указаны только неинверсные аргументы. Это значит, что
буква A не пишется, но подразумевается. То же самое относится и к букве B.
Она занимает верхнюю половину карты. Нижняя половина соответствует ин-
версной переменной .
B
Возможны и другие способы расположения букв вокруг карты. Напри-
мер, на рисунке 5.4 показана карта для случая, когда зона действия буквы A
находится не слева, а справа. Расположение минтермов вследствие этого изме-
нилось. Перебором нетрудно установить, что всего существует восемь вариан-
тов построения карты Вейча двух переменных.
A
A
A
A
B
B
AB
AB
AB
AB
A
B
1
1
1