ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16682
Скачиваний: 202
111
Рис. 5.4
Рис. 5.5
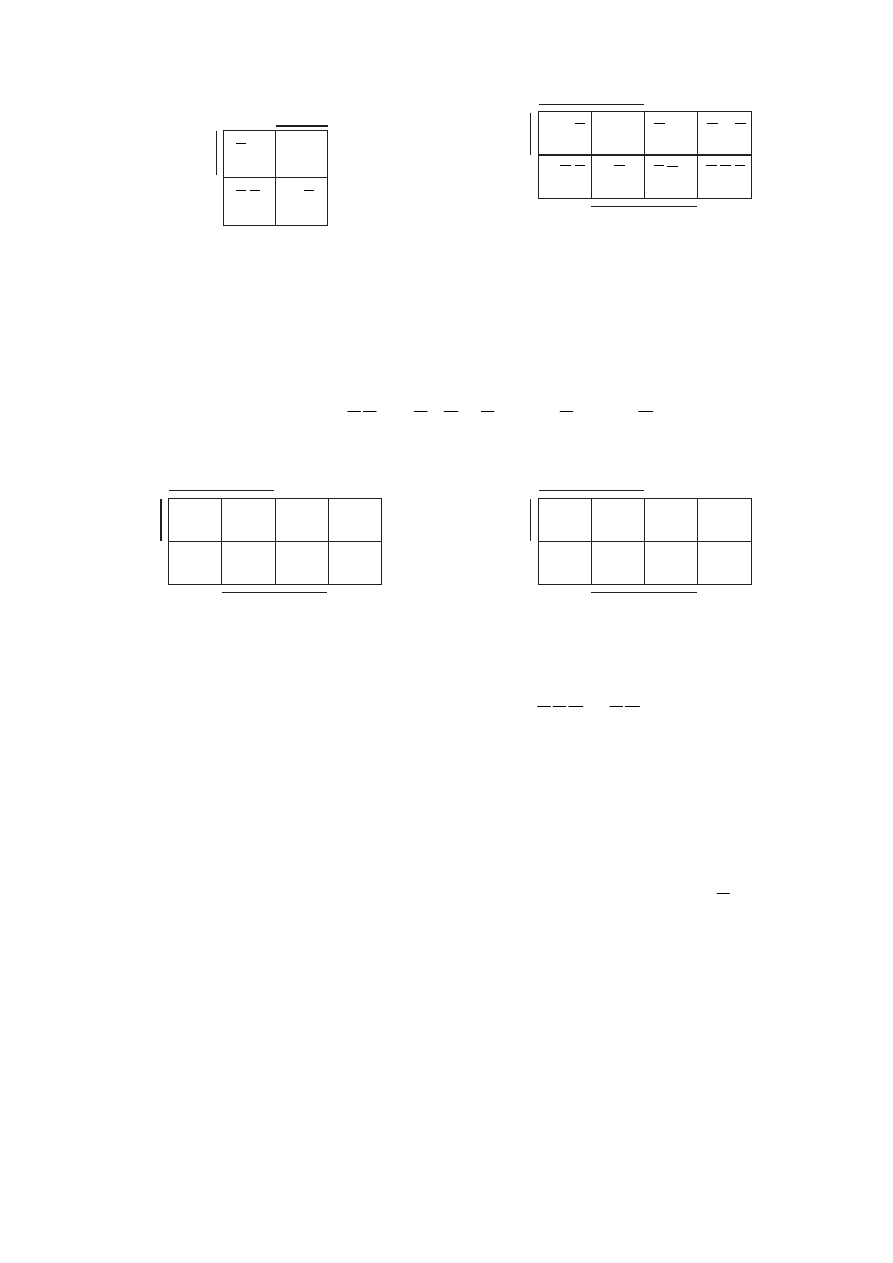
На рисунке 5.5 изображена карта Вейча трёх аргументов. В ней также для
каждого минтерма отведена одна клетка. На рисунке 5.6 представлена та же
карта, но в клетках указаны десятичные номера минтермов. На рисунке 5.7
приведена карта трёх переменных с нанесённой на неё булевой функцией вида
.
)
,
,
(
C
AB
C
B
A
BC
A
C
B
A
C
B
A
C
B
A
f
+
+
+
+
=
Рис. 5.6
Рис. 5.7
Единицы на этой карте говорят о том, что соответствующие минтермы
входят в заданную функцию. Три минтерма –
ABC
C
B
A
C
B
A
,
,
– в записи
функции отсутствуют. По этой причине в клетках с номерами 0, 4, 7 единиц нет
(если клетка пуста, то предполагается, что в ней стоит нуль).
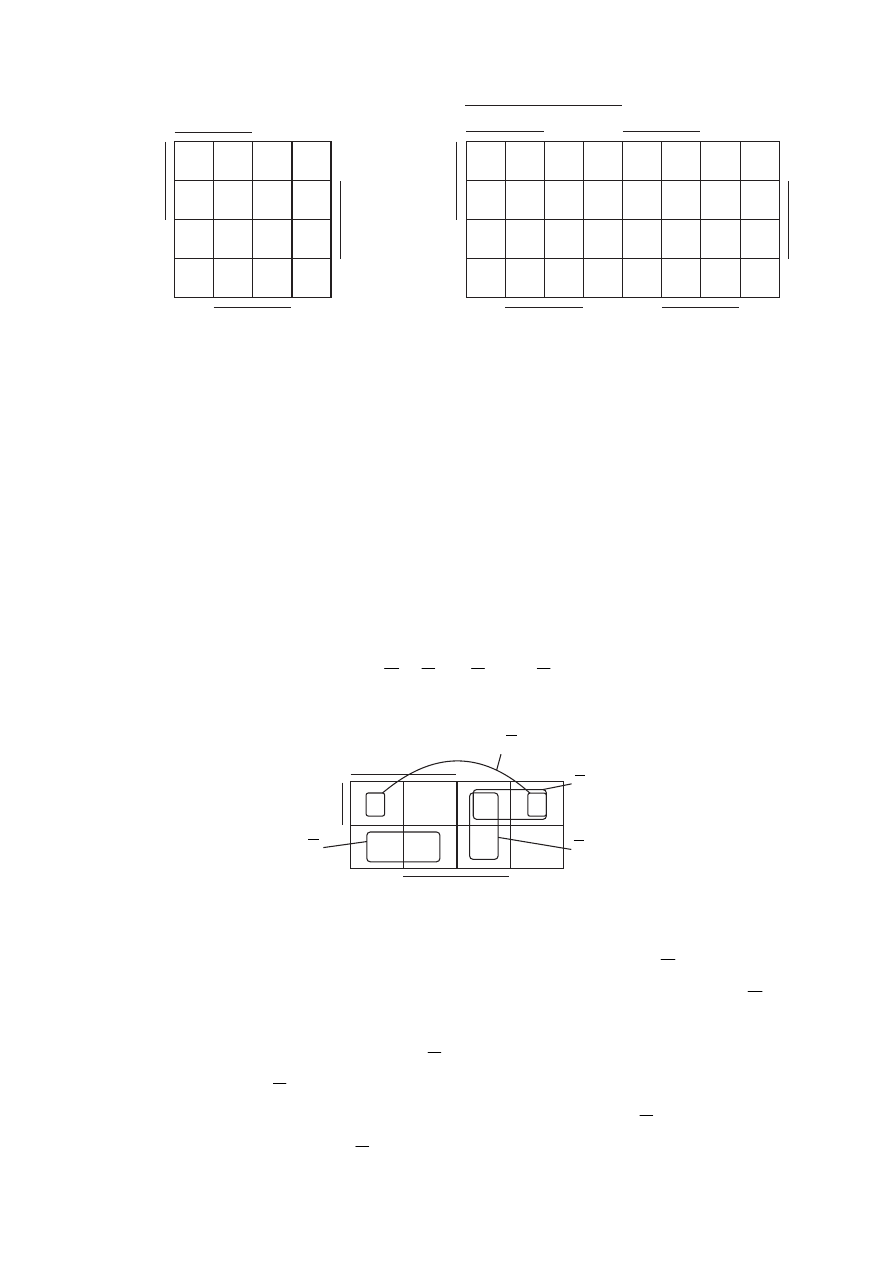
На рисунке 5.8 представлена карта четырёх аргументов, где в клетках
указаны минтермы в их цифровой записи. На рисунке 5.9 изображена карта пя-
ти аргументов. Она получена из двух карт четырёх аргументов, приставленных
одна к другой. Левая карта обозначена буквой E, а правая – буквой .
E
Анало-
гичным образом можно построить карту на любое число аргументов.
Карта Вейча может быть построена многими способами. Если выбрана
конфигурация, то одна карта от другой отличается только расположением букв.
В данной книге в качестве эталонных приняты карты Вейча, приведённые на
рисунках 5.2, 5.6, 5.8, 5.9.
A
B
AB
AB
AB
AB
A
B
ABC
ABC
C
ABC ABC
ABC ABC ABC ABC
A
B
7
C
5
6
4
3
1
2
0
A
B
C
1
1
1
1
1
112
Рис. 5.8
Рис. 5.9
5.5 Нанесение булевых функций на карту Вейча
Работа с картой Вейча всегда начинается с нанесения на неё булева вы-
ражения. Если функция представлена в СДНФ, то нанесение её на карту сво-
дится к отысканию клеток, за которыми закреплены номера соответствующих
минтермов. В найденные клетки ставятся единицы, как показано на рисун-
ках 5.3 и 5.7.
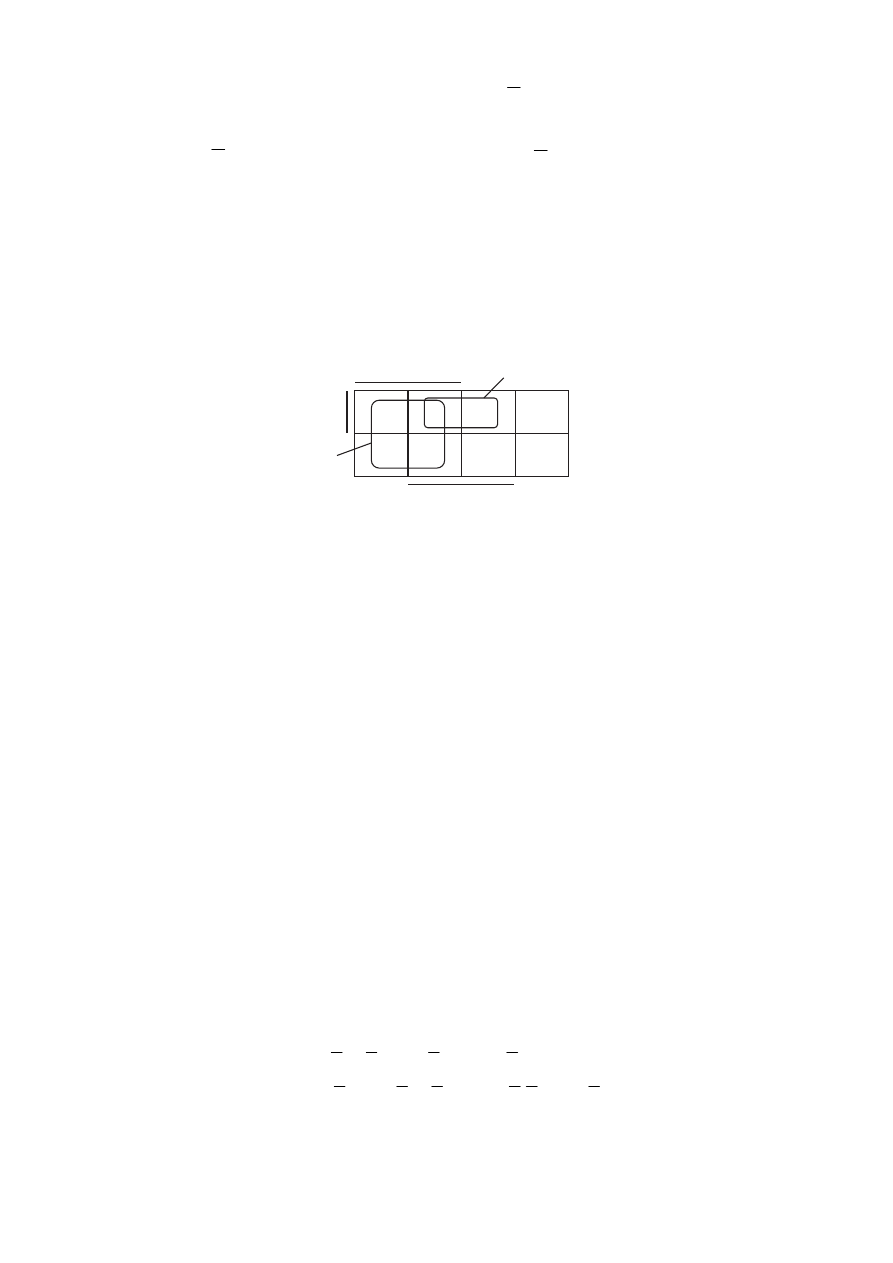
На карту можно нанести функцию, заданную не только в СДНФ, но и в
виде произвольной ДНФ. Например, нанесём на карту Вейча функцию
(рис. 5.10):
.
B
A
C
A
B
A
C
B
f
+
+
+
=
(5.4)
Рис. 5.10
Первая конъюнкция, входящая в функцию, имеет вид
.
C
B
Соответству-
ющая ей область карты находится на пересечении зон действия букв B и .
C
Это
две верхние клетки по концам строки. В них ставим единицы.
Вторая конъюнкция имеет вид
.
B
A
Находим область на карте, являющу-
юся общей для зон A и B. Ставим в них единицы. Правая клетка уже занята,
поэтому единицу ставим только на свободное место области
.
B
A
Наносим конъюнкцию
.
C
A
Она на карте занимает две вертикально рас-
A
B
C
12
D
14
6
4
13 15
7
5
9
11
3
1
8
10
2
0
A
B
C
25 29 13
9
27 31 15 11
19 23
7
3
17 21
5
1
A
C
24
D
28 12
8
26 30 14 10
18 22
6
2
16 20
4
0
E
A
B
C
1
1
1
1
1
1
BC
AB
AC
AB
113
положенные клетки на пересечении области A с областью C. И здесь ставим
только одну единицу, так как одна единица уже поставлена при нанесении
конъюнкции
.
B
A
Осталась одна конъюнкция
.
B
A
Она занимает в области A
две нижние клетки. В них ставим единицы.
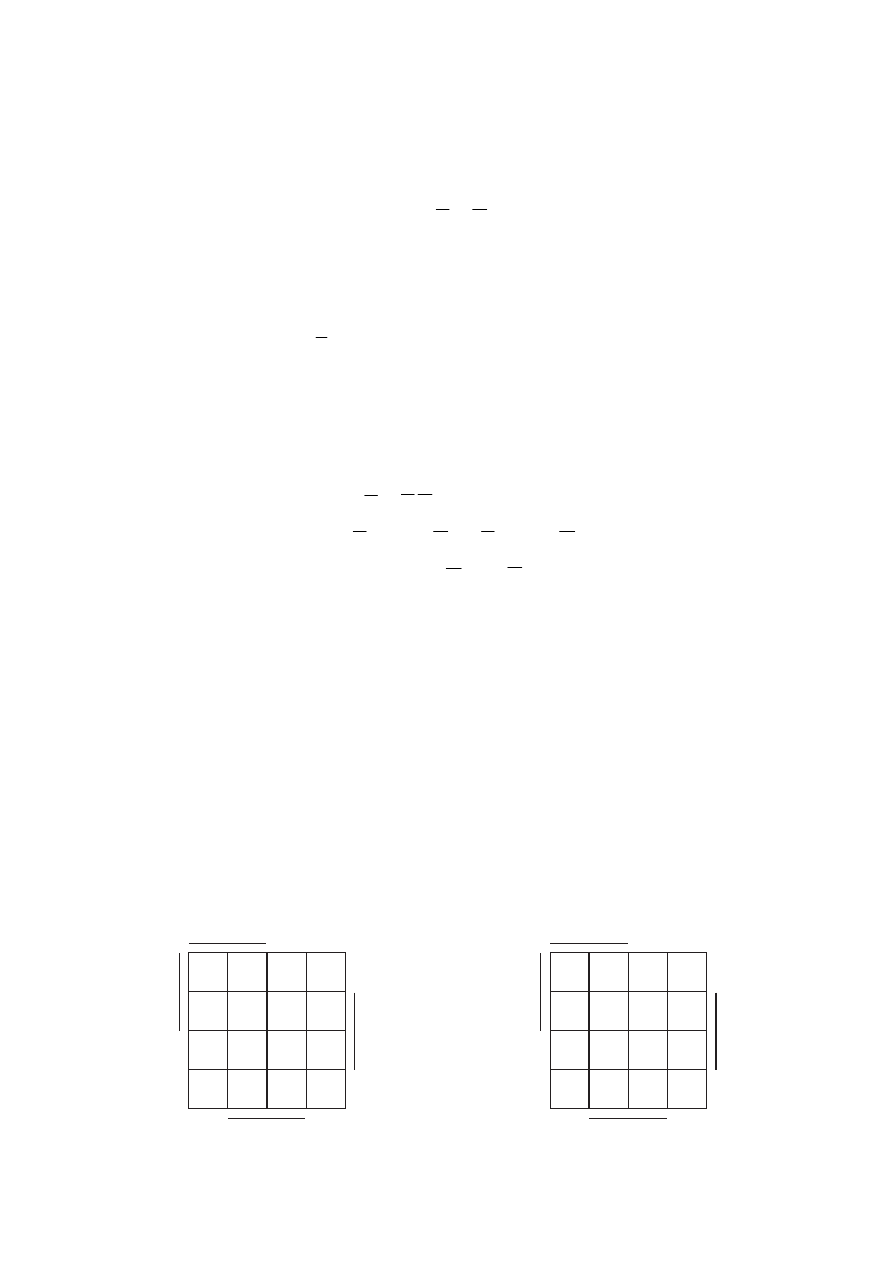
Рассмотрим еще один пример. Нанесём на карту функцию
.
= +
f
A
BC
(5.5)
Первое слагаемое состоит из одной буквы A. Ей соответствует область A
из четырех клеток, следовательно, всю её заполняем единицами (рис. 5.11).
Рис. 5.11
Конъюнкции BC на карте соответствует область на пересечении зон, от-
носящихся к буквам B и C. Эту область заполняем единицами. Заметим, что
седьмой минтерм отмечен при нанесении буквы A. Вторично его не отмечаем.
При помощи карты Вейча легко найти СДНФ функции, если она пред-
ставлена в ДНФ. Для этого наносим функцию на карту, а затем мысленно
наложим на неё стандартную карту. Единицы покажут, какие номера минтер-
мов входят в заданную функцию. Например, найдём СДНФ функции (5.4). Её
карта Вейча изображена на рисунке 5.10. Сопоставив её с рисунком 5.6, полу-
чаем СДНФ:
f
(A,B,C) = (1, 2, 3, 4, 5, 6).
Точно таким же образом находим СДНФ функции (5.5):
f
(A,B,C) = (3, 4, 5, 6, 7).
5.6 Операции над функциями, представленными в СДНФ
С помощью карт Вейча легко выявить равенство двух функций. Две
функции тождественно равны, если их СДНФ совпадают. Например, функции
1
2
;
=
+
+
+
=
+
+
+
+
f
ABD
ABC
BCD
ACD
f
ABC
BCD
ACD
AB CD
ABCD
внешне не имеют ничего общего, но если их нанести на карту Вейча четырёх
аргументов, то окажется, что их СДНФ совпадают. Следовательно, f
1
= f
2
.
A
B
C
1
1
1
1
1
A
BC
114
Карты Вейча позволяют находить СДНФ инверсий функций, их дизъюнк-
ции и конъюнкции. Чтобы найти СДНФ инверсии функции f, достаточно эту
функцию нанести на карту Вейча. Номера минтермов, которым соответствуют
пустые клетки на карте, дадут искомую инверсию. Например, СДНФ функции
,
D
C
B
A
f
+
=
зависящей от четырёх переменных, имеет вид:
f
= (1, 5, 8, 9, 10, 11, 13).
Минтермы, соответствующие пустым клеткам, дают СДНФ инверсии:
f
= (0, 2, 3, 4, 6, 7, 12, 14, 15).
Чтобы найти СДНФ конъюнкции n функций, достаточно все их нанести
на одну и ту же карту независимо одна от другой. В некоторых клетках может
оказаться n единиц. Выписав номера клеток с n единицами, мы получим СДНФ
конъюнкции n заданных функций. Например, пусть заданы три функции:
;
1
ABC
D
C
A
B
A
f
+
+
=
;
2
D
AB
C
B
D
C
A
BC
A
f
+
+
+
=
.
3
C
AB
D
AC
BCD
f
+
+
=
Соответствующие им карты Вейча приведены на рисунках 5.12, 5.13 и
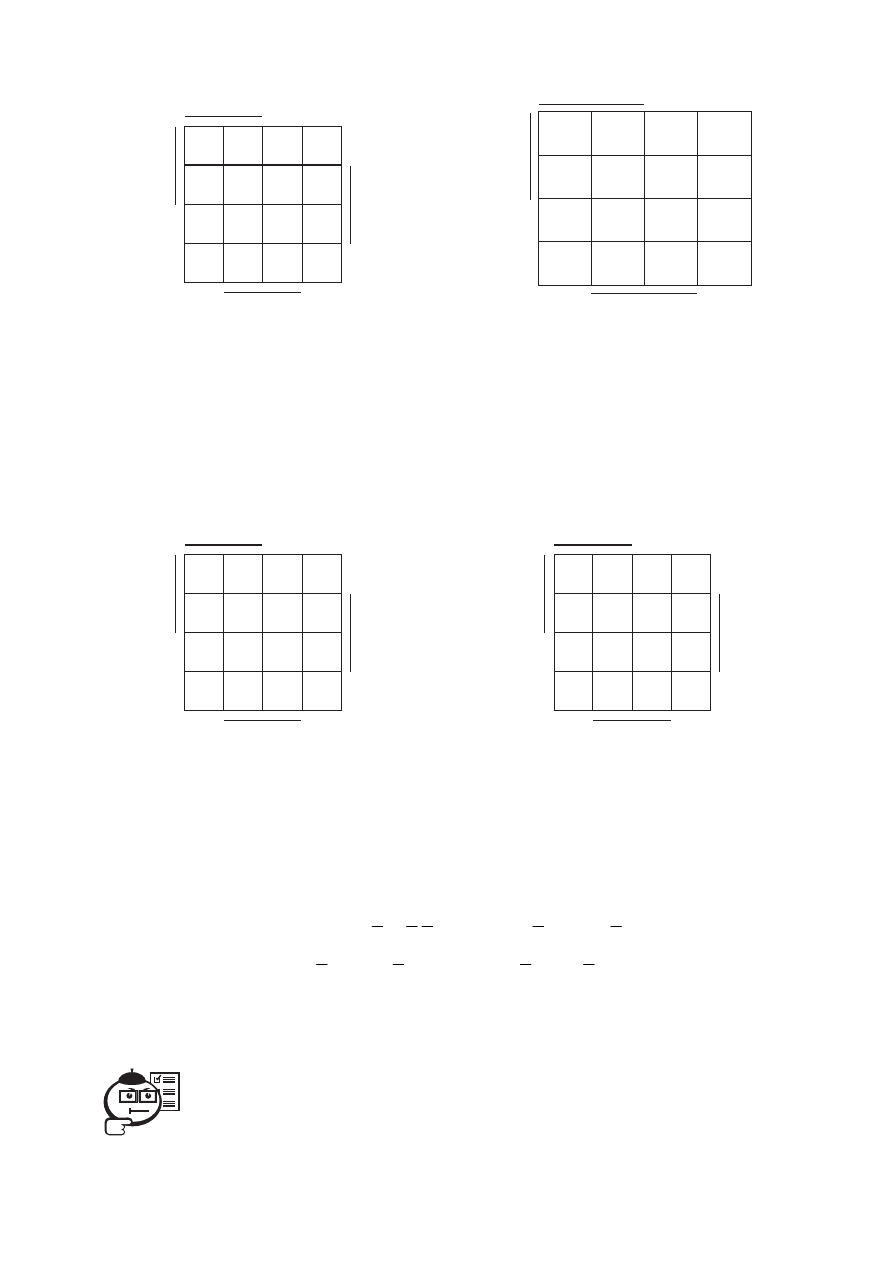
5.14. Единицы со всех трёх карт перенесём на одну карту вместе с нулями, как
показано на рисунке 5.15. Например, 12-й минтерм на рисунке 5.12 отсутствует
(напомним, что пустой клетке соответствует нуль). А на рисунках 5.13 и 5.14 на
месте 12-го минтерма стоят единицы. Поэтому в той же области на рисун-
ке 5.15 ставим последовательность 011. Минтерм 14 отмечен единицами на
всех картах. В соответствии с этим на рисунке 5.15 записываем последователь-
ность 111. На месте четвёртого минтерма во всех трёх картах единиц нет. Сле-
довательно, на рисунке 5.15 этот минтерм обозначаем последовательно-
стью 000.
Рис. 5.12
Рис. 5.13
A
B
C
D
1
1
1
1
1
1
1
1
A
B
C
1
D
1
1
1
1
1
1
1
1
1
115
Рис. 5.14
Рис. 5.15
Аналогично рассуждая, заполняем всю карту. На ней имеется только две
клетки с тремя единицами. Это места минтермов 10 и 14, образующих конъ-
юнкцию всех трёх функций (рис. 5.16):
1 2 3
(10,14).
f f f =
Рис. 5.16
Рис. 5.17
Для нахождения СДНФ дизъюнкции двух и более функций все их после-
довательно наносим на одну и ту же карту Вейча. Например, чтобы найти
СДНФ дизъюнкции предыдущих трёх функций, на карту Вейча наносим сле-
дующее выражение:
1
2
3
+
+
=
+
+
+
+
+
f
f
f
AB
ACD
ABC
ABC
ACD
.
+
+
+
+
+
BC
ABD
BCD
ACD
ABC
Искомая СДНФ имеет вид (рис. 5.17):
f
1
+ f
2
+ f
3
= (1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15).
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Укажите номер той клетки карты Вейча, где записывается
минтерм:
A
B
C
1
D
1
1
1
1
1
A
B
111
101
011
011
010
011
000
100
110
C
1 1
1
110
100
010
010
100
000
A
B
C
D
1
1
A
B
C
1
D
1
1
1
1
1
1
1
1
1
1
1
1
1