ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16683
Скачиваний: 202

116
1) ABC;
3) B
A
;
5)
DE
C
B
A
;
2)
D
C
AB
;
4)
D
C
B
A
;
6)
F
E
D
BC
A
.
2.
Сколько клеток на карте Вейча пяти аргументов?
3.
Сколько клеток на карте Вейча десяти аргументов?
4.
Нанесите функцию на карту Вейча четырёх аргументов.
Определите число клеток, занятых единицами:
1)
;
D
C
AB
f
+
=
3)
;
D
A
f
+
=
5)
;
D
C
AB
f
+
+
=
2)
;
D
A
ABCD
f
+
=
4)
;
C
B
A
f
+
+
=
6) f = A + C.
5.
Нанесите функции на карту Вейча четырёх аргументов.
Сколько минтермов содержится в СДНФ их инверсий?
1) f = AB; 3)
;
D
C
B
A
f =
5)
;
C
B
A
f
+
=
2)
;
CD
B
A
f
+
+
=
4)
;
D
C
B
A
f
+
+
+
=
6)
.
D
ABC
f
+
=
6.
Сколько клеток займёт функция
,
B
A
f =
если её нанести на
карту трёх аргументов? Четырёх аргументов? Пяти аргументов?
Шести аргументов?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
5.7 Минимизация ДНФ при помощи карт Вейча
Минимизация при помощи карт Вейча сводится к нахождению наимень-
шего числа простых импликант, но не всех возможных, а только тех, которые
все вместе объединяют все единицы на карте.
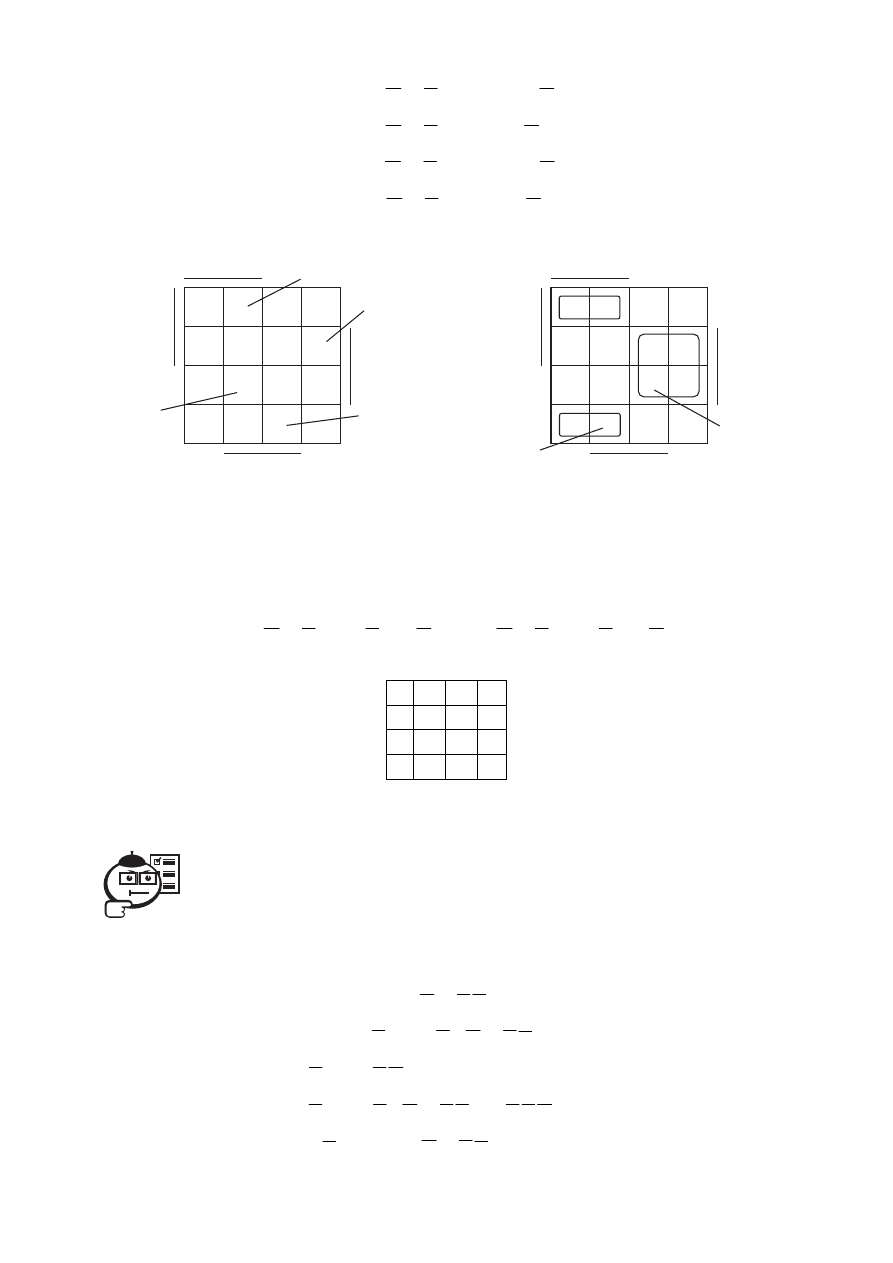
Начинать минимизацию следует с единиц, входящих в единственную
простую импликанту. Обратимся к карте, изображённой на рисунке 5.18. На
ней имеются только три единицы, с которых следует начинать упрощение
функции. Это минтерм m
2
, входящий в единственную простую импликанту
,
C
B
затем минтерм m
5
, входящий в единственную простую импликанту
,
D
B
A
и минтерм m
14
, входящий в простую импликанту AC. Начинать минимизацию с
других единиц не следует, так как каждая из них входит более чем в одну про-
стую импликанту, вследствие чего можно выбрать «не ту» импликанту и тогда
минимальная форма не будет найдена.
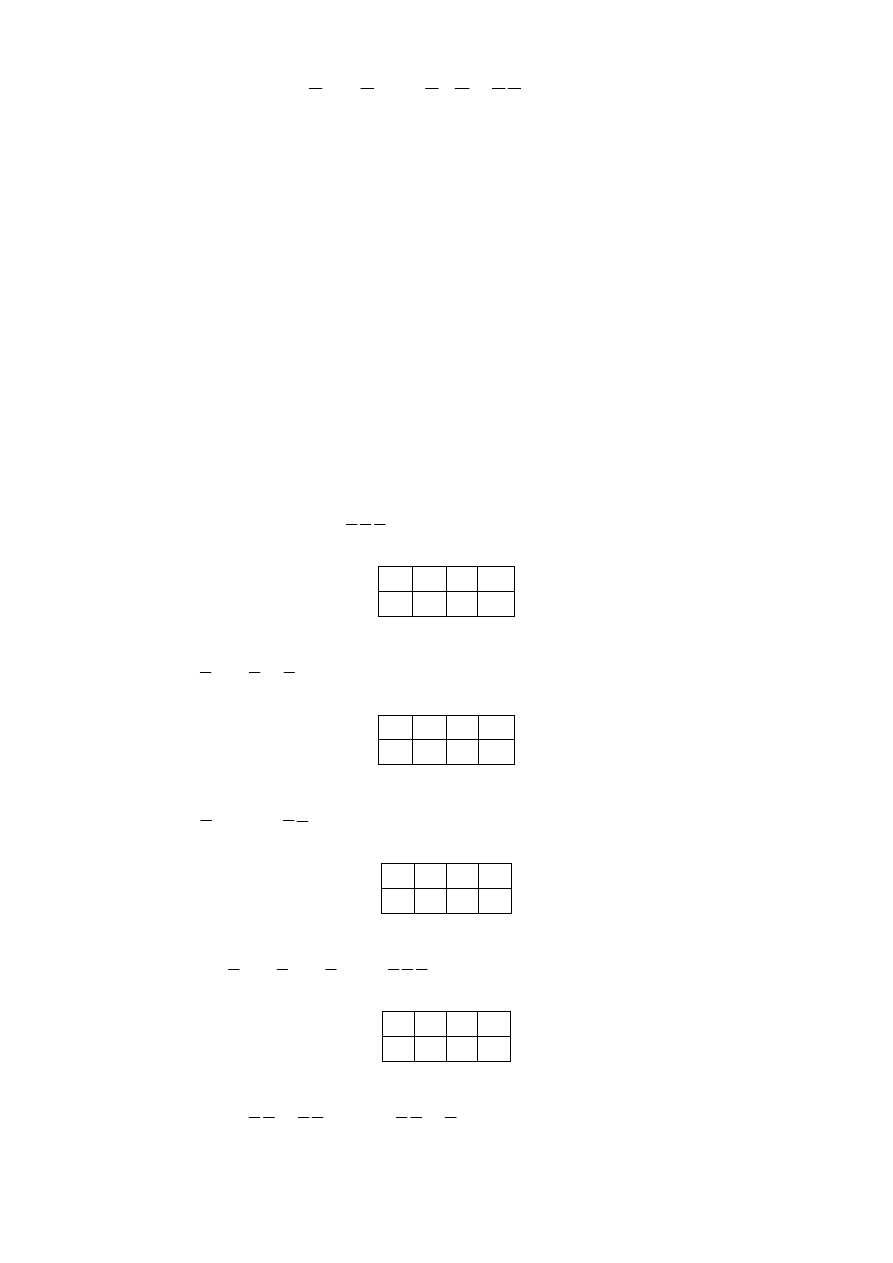
На рисунке 5.19 приведена карта, на которой только два минтерма входят
в единственные простые импликанты. Это минтермы m
3
и m
10
. Соответст-
вующие им простые импликанты обведены. На карте остались три единицы.
Объединить их можно различными вариантами:
117
;
C
A
AB
D
A
D
A
f
+
+
+
=
;
D
C
AB
D
A
D
A
f
+
+
+
=
;
C
A
BD
D
A
D
A
f
+
+
+
=
.
D
C
BD
D
A
D
A
f
+
+
+
=
Рис. 5.18
Рис. 5.19
Таким образом, данная функция (рис. 5.19) имеет 4 минимальные формы.
На рисунке 5.20 представлена функция, минимальная ДНФ которой имеет
два варианта записи:
;
C
A
B
A
B
A
D
f
+
+
+
=
.
C
B
B
A
B
A
D
f
+
+
+
=
1 1 1 1
1 1 1
1 1
1 1 1 1
Рис. 5.20
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Сколько простых импликант и сколько вхождений пере-
менных содержат минимальные ДНФ следующих функций, зави-
сящих от трёх переменных?
1)
;
C
B
A
C
B
BC
AB
f
+
+
+
=
2)
;
C
B
A
C
B
A
BC
A
ABС
f
+
+
+
=
3)
;
C
B
A
B
A
f
+
=
4)
;
C
B
A
C
B
A
C
B
A
BС
A
f
+
+
+
=
5)
;
C
B
A
C
B
BC
B
A
f
+
+
+
=
A
B
C
D
1
1
1
1
1
1
1
1
m
14
m
5
m
2
m
11
A
B
C
1
D
1
1
1
1
1
1
1
1
1
1
m
3
m
10
118
6)
.
C
B
A
C
B
A
BC
A
С
A
f
+
+
+
=
2.
Сколько простых импликант и сколько вхождений пере-
менных содержится в минимальных ДНФ функций четырёх пере-
менных?
1) f = (0, 1, 2, 3, 7, 11, 12, 13, 14, 15);
2) f = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 15);
3) f = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15).
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
5.8 Примеры минимизации ДНФ булевых формул
при помощи карт Вейча
В данном параграфе приведены образцы решения задач по минимизации
булевых формул. Расположение букв вокруг карт Вейча, как на рисунках 5.6,
5.8, 5.9.
1.
f
AB
BC
AC
ABC
=
+
+
+
(рис. 5.21).
1 1 1
1
1
Рис. 5.21
2.
f
A
BC
BC
= +
+
(рис. 5.22).
1
1 1
1 1 1
Рис. 5.22
3.
f
C
AB
AB
= +
+
(рис. 5.23).
1 1 1
1 1 1
Рис. 5.23
4.
f
ABC
ABC
ABC
ABC
=
+
+
+
(рис. 5.24).
1 1
1 1
Рис. 5.24
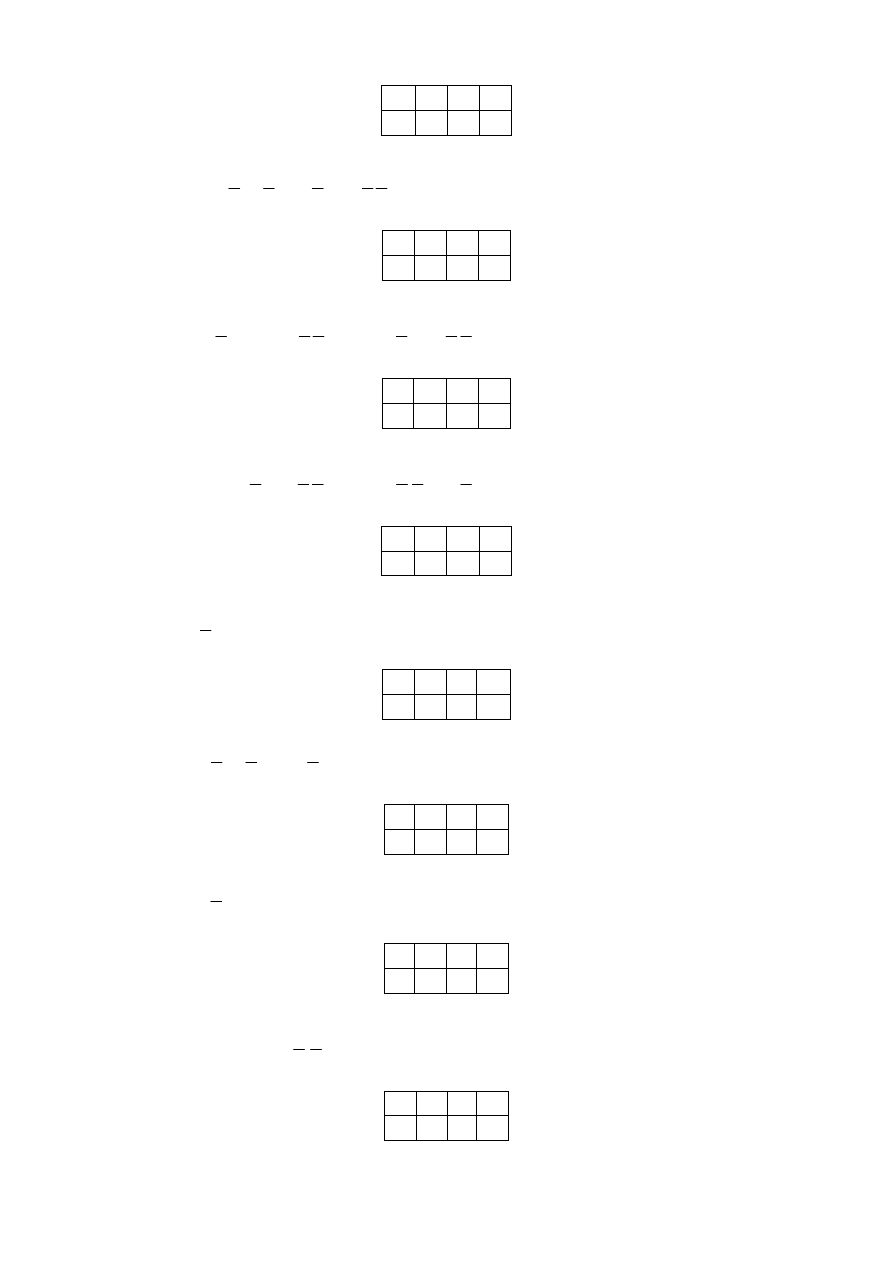
5.
f
BC
BC
AB
BC
BC
AC
=
+
+
=
+
+
(рис. 5.25).
119
1 1
1
1 1
Рис. 5.25
6.
f
ABC
BC
AC
AB
=
+
+
+
(рис. 5.26).
1 1
1 1 1
Рис. 5.26
7.
f
AC
BC
AB
AB
AC
BC
=
+
+
=
+
+
(рис. 5.27).
1 1 1
1 1 1
Рис. 5.27
8.
f
AC
AB
BC
BC
AC
AB
=
+
+
=
+
+
(рис. 5.28).
1 1 1
1 1 1
Рис. 5.28
9.
f
B
C
= +
(рис. 5.29).
1 1
1 1 1 1
Рис. 5.29
10.
f
C
AB
AB
= +
+
(рис. 5.30).
1 1 1
1 1 1
Рис. 5.30
11.
f
C
=
(рис. 5.31).
1
1
1
1
Рис. 5.31
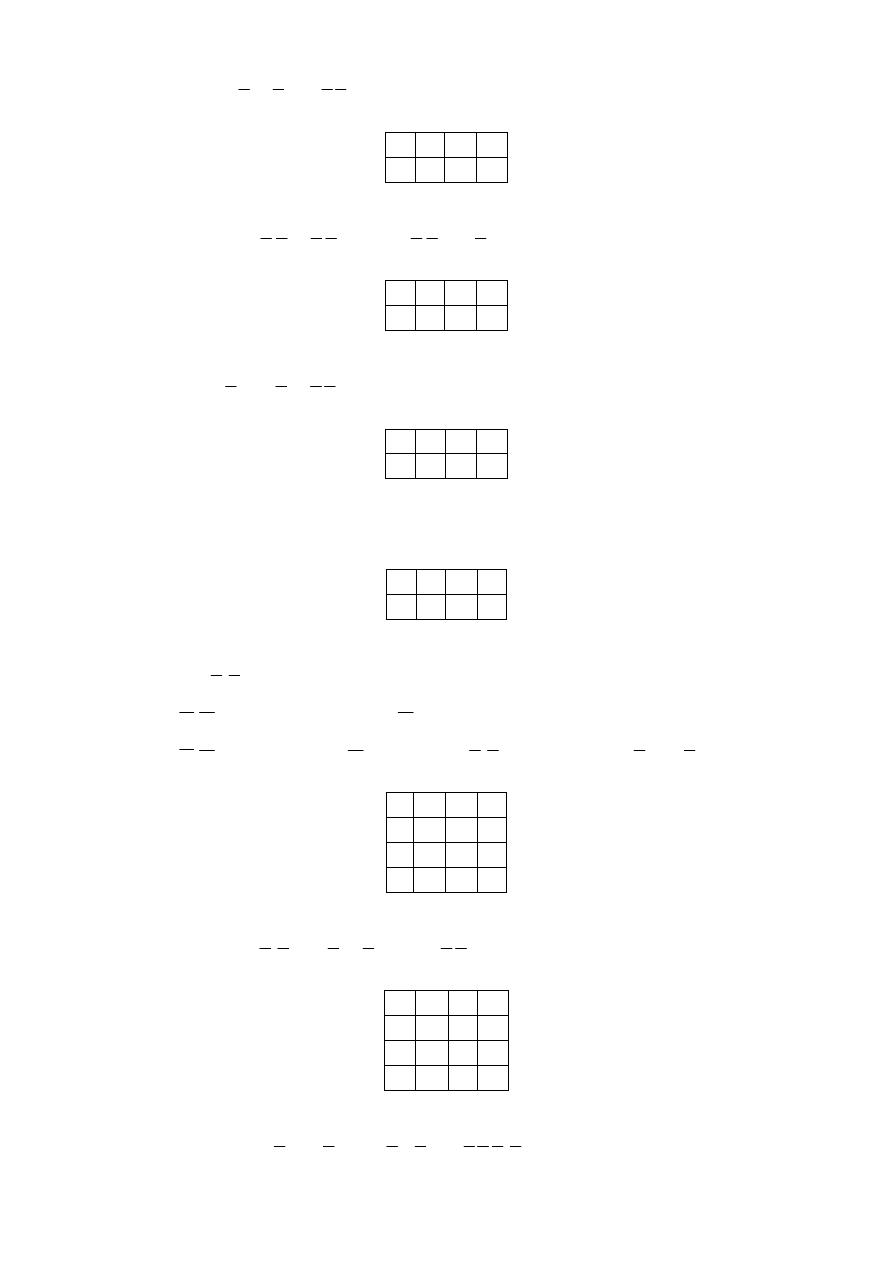
12.
f
C
AB
A B
= +
+
(рис. 5.32).
1 1 1
1 1 1
Рис. 5.32
120
13.
f
ABC
BC
AB
=
+
+
(рис. 5.33).
1
1 1 1
Рис. 5.33
14.
f
AC
AC
BC
AC
AC
AB
=
+
+
=
+
+
(рис. 5.34).
1 1
1 1 1
Рис. 5.34
15.
f
BC
AC
ABC
=
+
+
(рис. 5.35).
1
1
1 1 1
Рис. 5.35
16.
1
f =
(рис. 5.36).
1 1 1 1
1 1 1 1
Рис. 5.36
17.
;
f
C D
CD
AB
BC
AC
=
+
+
+
+
;
D
A
BC
AB
CD
D
C
f
+
+
+
+
=
;
AC
D
B
AB
CD
D
C
f
+
+
+
+
=
f
C D
CD
AB
BD
AD
=
+
+
+
+
(рис. 5.37).
1 1 1 1
1 1 1
1 1
1 1 1
Рис. 5.37
18.
f
BC
C D
AD
ACD
ABC
=
+
+
+
+
(рис. 5.38).
1 1 1 1
1 1
1 1
1 1 1
Рис. 5.38
19.
f
AC
ABD
BCD
ABCD
ABC D
=
+
+
+
+
(рис. 5.39).