ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16654
Скачиваний: 202
181
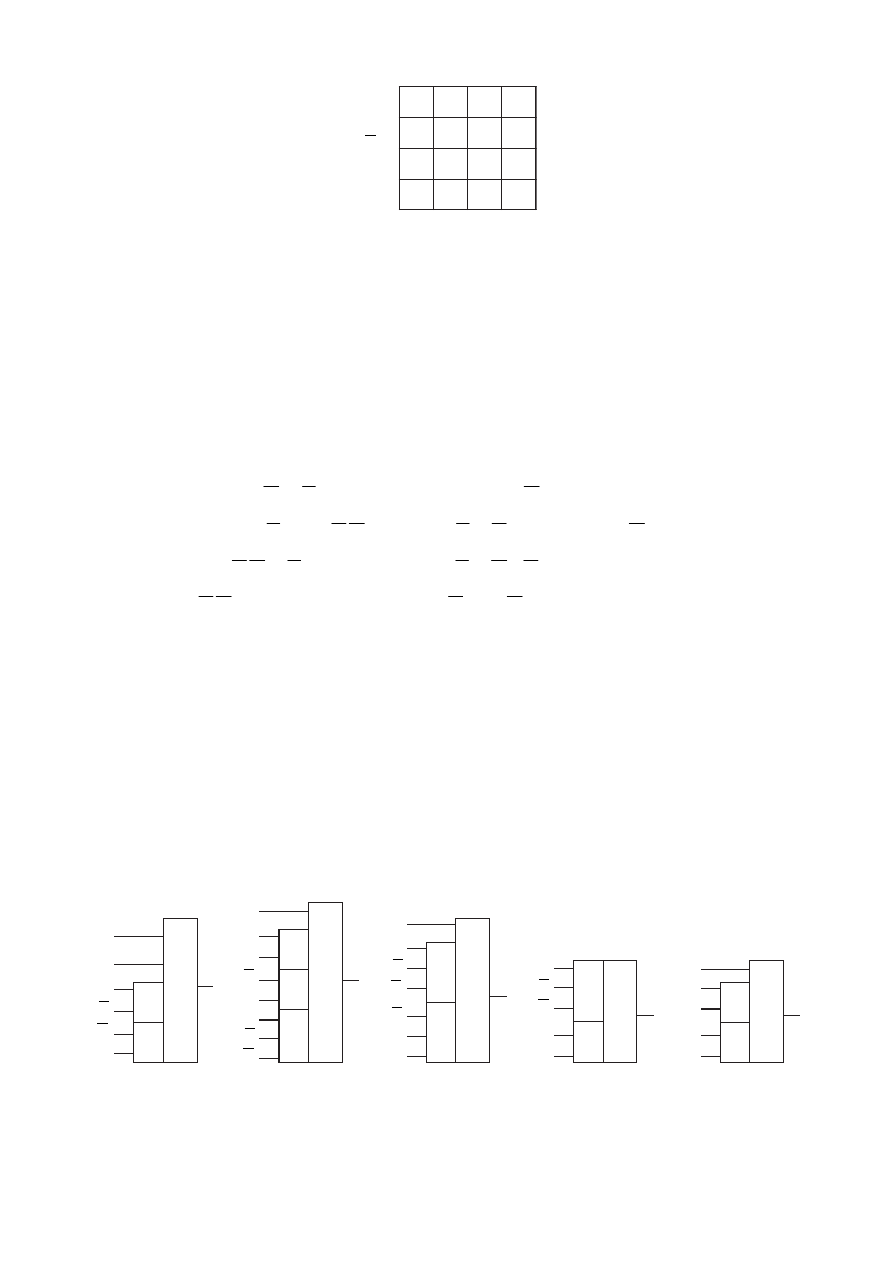
Рис. 8.22
Остальные функции в СДНФ имеют вид (неопределённые состояния
остаются теми же).
f
2
= (2, 3, 4, 7, 8, 9);
f
3
= (3, 4, 8, 9);
f
4
= (4, 9);
f
5
= (5, 6, 7, 8, 9).
Полный список минимальных ДНФ и КНФ имеет вид:
;
1
D
B
D
B
C
A
f
+
+
+
=
);
)(
(
1
C
B
A
D
C
A
f
+
+
+
+
=
;
2
D
C
B
C
B
CD
A
f
+
+
+
=
);
)(
)(
(
2
C
B
A
D
C
A
D
C
B
f
+
+
+
+
+
+
=
;
3
CD
B
D
C
B
A
f
+
+
=
);
)(
)(
(
3
C
B
A
D
C
D
B
f
+
+
+
+
=
;
4
AD
D
C
B
f
+
=
);
)(
(
4
D
B
D
A
C
f
+
+
=
;
5
BD
BC
A
f
+
+
=
).
)(
(
5
D
C
A
B
A
f
+
+
+
=
Для построения логической схемы преобразователя выбираем те функ-
ции, которые в аналитическом представлении содержат наименьшее число
букв. Если ДНФ и КНФ по числу букв одинаковы, то берем ДНФ.
В данном случае во всех КНФ число букв не меньше, чем в ДНФ. Схема
преобразователя приведена на рисунке 8.23. Все пять её составляющих постро-
ены на основе минимальных дизъюнктивных нормальных форм булевых функ-
ций.
Рис. 8.23
1
f
1
=
1
×
×
×
×
×
×
f
1
&
&
1
A
C
B
D
D
B
f
2
&
&
1
A
C
B
D
B
C
&
D
C
f
3
&
1
A
C
B
D
B
C
&
D
f
4
&
1
A
B
D
C
&
D
f
5
&
1
B
A
D
&
C
B

182
8.9 О путях дальнейшего упрощения комбинационных схем
Информации, представленной в данной главе, вполне достаточно для то-
го, чтобы разработать практически любую электронную комбинационную
структуру, работа которой представима в виде таблицы истинности. Все такие
структуры можно рассматривать как преобразователи n-значных двоичных ко-
дов в m-значные.
Наиболее простым является случай, когда m = 1, т. е. схема содержит
только один выход. Её синтез сводится к минимизации булевой функции в
ДНФ и КНФ. При возможности следует уменьшить число букв повышением
порядка формул, если это допускается по условиям быстродействия схемы.
Если m > 1, то выход преобразователя представляет собой систему буле-
вых функций. В этих случаях продолжить упрощение схемы можно за счёт вы-
явления одинаковых составляющих, входящих в несколько функций. Эти оди-
наковые составляющие в схеме реализуются один раз, а используются
многократно. Например, конъюнкция
D
C
B
входит одновременно в формулы
f
2
, f
3
и f
4
п. 8.8. Следовательно, два трёхвходовых элемента И из схемы
(рис. 8.23) можно удалить.

183
9 Функциональная полнота системы
булевых функций
9.1 Вводные замечания
На заре развития цифровой техники электронные схемы строили из логи-
ческих элементов, используя для них диоды, транзисторы, резисторы. Со вре-
менем появились идеи представления логических элементов в виде неразбор-
ных блоков (модулей, позже – микросхем), реализующих некоторые булевы
функции. И тут стали возникать вопросы: какие следует выбирать функции для
реализации их в неразборном представлении? Каков минимальный набор бло-
ков? Может быть достаточно одной микросхемы, позволяющей строить любые
логические схемы и запоминающие элементы – триггеры, и как убедиться в его
универсальности? Всякая ли булева функция с применением операции суперпо-
зиции может быть реализована из микросхемных блоков? На все подобные во-
просы ответы даёт теорема Поста о функциональной полноте (в литературе её
иногда называют теоремой Поста – Яблонского, например в [14]).
Основу понятия функциональной полноты составляют пять классов буле-
вых функций: монотонные, линейные, самодвойственные, сохраняющие нуль и
сохраняющие единицу. Им посвящён данный раздел, где рассмотрены не толь-
ко эти классы, но и приведена теорема Поста, являющаяся завершением темы
синтеза комбинационных и многотактных схем дискретного действия.
9.2 Монотонные функции
Булева функция n аргументов называется монотонной, если при любом
возрастании сравнимых наборов функция не убывает. В сравнимых наборах a и
b выполняется неравенство: a
i
≥ b
i
(i = 1, 2, …, n; i – номер разряда двоичного
набора). На несравнимых наборах монотонная функция может убывать или
оставаться неизменной. Например, функция f = AB + C на несравнимых набо-
рах 001 и 010 убывает, а на наборах 101 и 110 не изменяется. На сравнимых
наборах 100 и 111 возрастает и не изменяется на наборах 001 и 101.
Всякая монотонная функция имеет единственную минимальную ДНФ и
единственную минимальную КНФ, причем обе формы не содержат инверсных
аргументов. Например, в результате минимизации функции
f = (3, 5, 7, 10, 11, 12, 13, 14, 15)

184
получаем минимальные ДНФ и КНФ без инверсий:
f = AB + AC + BD + CD; f = (A + D)(B + C),
следовательно, эта функция является монотонной.
Верно и обратное утверждение: если в аналитической записи функции от-
сутствуют инверсные аргументы, то функция является монотонной. Эти свой-
ства можно использовать в качестве критерия при исследовании функций на
монотонность.
Монотонные функции образуют функционально замкнутый класс, т. е. в
результате суперпозиции монотонных функций всегда будут получаться только
монотонные функции.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Укажите номера функций, являющихся монотонными:
1) f = 0; 2) f = A+B; 3) f = A +A; 4) f = AB; 5) f =
C
A
C
A
+
.
2. Какие функции являются монотонными? Укажите их номе-
ра:
1) f = C
A
; 2) f = A⊕B; 3) f = 1⊕AB; 4) f = ABC; 5) f =
.
C
A +
3. Какие функции являются немонотонными? Укажите их но-
мера:
1) f =
B
A +1; 2) f = 1·0·A+B; 3) f = 1⊕ C
A
; 4) f = C
A
;
5) f =
.
C
A +
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
9.3 Линейные функции
Функция называется линейной, если в алгебре Жегалкина она представи-
ма в виде полинома первой степени (без конъюнкций). Например, функции
f
1
= A ⊕
B, f
2
= A ⊕
B ⊕ C ⊕ 1, f
3
= B ⊕ 1, f
4
= 1, f
5
= 0
не содержат конъюнкций, следовательно, являются линейными. Функция
f = AС ⊕ B
содержит конъюнкцию, поэтому к классу линейных не относится.
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 9.1
· · · · · · · · · · · · · · · · · · · · · · ·
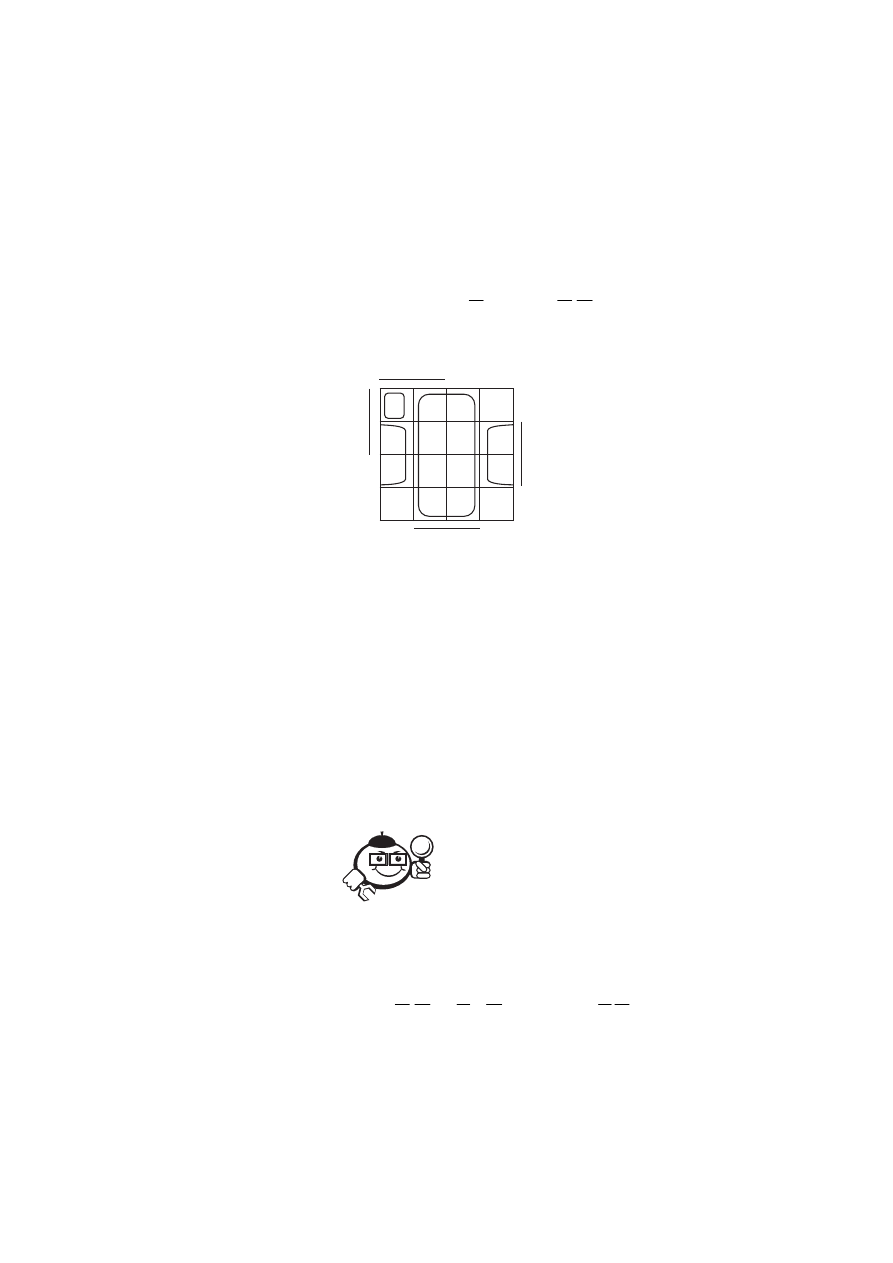
Является ли линейной функция
( , , , )
?
f A B C D
A B C D
ABCD
C
D
=
+
+ +
185
Находим полином Жегалкина. Для этого функцию представим в виде
дизъюнкции непересекающихся конъюнкций (напомним, что две конъюнкции
не пересекаются, если их произведение равно нулю). Преобразования можно
выполнить с применением формул (6.8)–(6.12), но проще применить карту Вей-
ча (рис. 9.1). Минтермы на этой карте сгруппированы так, что образуют непе-
ресекающиеся конъюнкции. Так как конъюнкции не пересекаются, то их со-
единяем знаками суммы по модулю 2:
.
)
,
,
,
(
D
C
B
A
D
C
C
D
C
B
A
f
⊕
⊕
=
Рис. 9.1
Устраняем знаки инверсии согласно формуле (6.12):
).
1
)(
1
(
)
1
(
)
,
,
,
(
⊕
⊕
⊕
⊕
⊕
=
D
C
B
A
D
C
C
D
C
B
A
f
Раскрываем скобки:
.
)
,
,
,
(
ABCD
ABD
ABC
B
A
D
CD
C
D
C
B
A
f
⊕
⊕
⊕
⊕
⊕
⊕
=
Полином Жегалкина содержит конъюнкции, следовательно, заданная
функция является нелинейной.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 9.2
· · · · · · · · · · · · · · · · · · · · · · ·
Определить, является ли линейной функция
f = (1, 2, 5, 6, 8, 11, 12, 15).
Действуем по аналогии с предыдущим случаем. По карте Вейча находим:
.
)
,
,
,
(
D
C
A
CD
A
D
C
A
D
C
A
D
C
B
A
f
⊕
⊕
⊕
=
Освобождаемся от знаков инверсии и находим полином Жегалкина:
=
⊕
⊕
⊕
⊕
⊕
⊕
⊕
⊕
⊕
=
D
C
A
CD
A
D
C
A
D
C
A
D
C
B
A
f
)
1
)(
1
(
)
1
(
)
1
(
)
1
)(
1
(
)
,
,
,
(
⊕
⊕
⊕
⊕
⊕
⊕
⊕
⊕
=
ACD
CD
AC
C
ACD
AD
AC
A
.
D
C
A
ACD
CD
AD
D
CD
A
⊕
⊕
=
⊕
⊕
⊕
⊕
⊕
A
B
D
C
1
1
1
1
1
1
1
1
1
1
1
1
1