ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16657
Скачиваний: 202

171
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. На рисунке 8.7 на вход подан низкий уровень напряжения.
Сколько вольт между эмиттером и коллектором транзистора?
2. На рисунке 8.7 падение напряжения на резисторе R равно
нулю. Сколько вольт между эмиттером и коллектором транзистора?
3. На рисунке 8.7 напряжение между точками A и f равно 5 В.
Найдите падение напряжения на резисторе R, если A = 0.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
8.5 Триггер типа RS
Изобретение бистабильного триггера (т. е. схемы с двумя устойчивыми
состояниями), составившего основу быстродействующей памяти средств авто-
матики и вычислительной техники, является одним из самых ярких и великих
достижений человечества. Изобрёл триггер в 1918 г. русский радиотехник, ос-
новоположник радиоламповой промышленности СССР Михаил Александрович
Бонч-Бруевич (1888–1940).
С тех пор специалистами было предложено много различных схем высо-
кого быстродействия для хранения информации в технических устройствах.
Среди них такие запоминающие элементы, как ферритовые кольца, трансфлюк-
соры, параметроны, криотроны и др. [13].
В настоящее время широчайшее распространение получили статические
триггеры. Простейшим из них является триггер типа RS. Он состоит из двух по-
следовательно соединённых элементов Шеффера, причем выход второго эле-
мента соединён со входом первого. Схема RS-триггера приведена на рисун-
ке 8.10, условное обозначение – на рисунке 8.11.
Рис. 8.10
Рис. 8.11
Триггер RS имеет парафазные выходы. Один из них называется прямым.
Обозначается он буквой без инверсии. Второй выход называется инверсным.
S
Q
R
Q
&
&
S
Q
R
Q

172
Обозначается буквой со знаком отрицания. На рисунке 8.10 прямой выход обо-
значен буквой Q, инверсный – буквой .
Q
В соответствии с вышепринятой ин-
терпретацией будем считать, что триггер находится в нулевом состоянии, если
на его прямом выходе имеется низкий уровень напряжения (тогда на инверс-
ном – высокий). Записывается это следующим образом: Q = 0. Триггер нахо-
дится в единичном состоянии, если на его прямом выходе поддерживается вы-
сокий уровень (а на инверсном – низкий). Записывается: Q = 1.
RS-триггер имеет два установочных входа: S – единичный, R – нулевой.
Исходное состояние входов: R = S = 1. Это режим хранения информации (объём
информации, хранимой одним триггером, – 1 бит). Если принять: R = 1, S = 0,
то триггер установится в единичное состояние. Если принять R = 0, S = 1, то
триггер перейдёт в нулевое состояние.
При R = S = 0 на обоих выходах будут высокие уровни напряжения.
В общем случае это состояние является запрещённым.
На рисунке 8.12 приведена схема RS-триггера, синхронизируемого по
входу C. Если на рисунке 8.10 триггер переходит, например, из нулевого в еди-
ничное состояние тотчас после подачи низкого уровня на вход S, то на рисун-
ке 8.12 триггер не меняет своего состояния при любых изменениях уровней
напряжения на входах R и S, если С = 0. Допустим, что Q = 0, кроме того, S = 1
и R = 0. Пока C = 0, триггер находится в нулевом состоянии. Лишь с момента,
когда на входе C напряжение переходит с низкого уровня на высокий, триггер
меняет своё состояние на единичное. Таким образом, синхронизируемый RS-
триггер переходит из одного состояния в другое только под действием синхро-
импульса. Происходит это в момент, когда напряжение на входе С меняется с
низкого уровня на высокий, а на переход синхроимпульса с высокого уровня на
низкий триггер не реагирует.
Рис. 8.12
Областью применения RS-триггеров является использование их в каче-
стве запоминающих регистров цифровых вычислительных устройств. Согласно
S
Q
R
Q
T
S
R
&
&
C
173
вышерассмотренной интерпретации булевых формул триггеры в этих регистрах
используются в качестве физических моделей логических переменных булевых
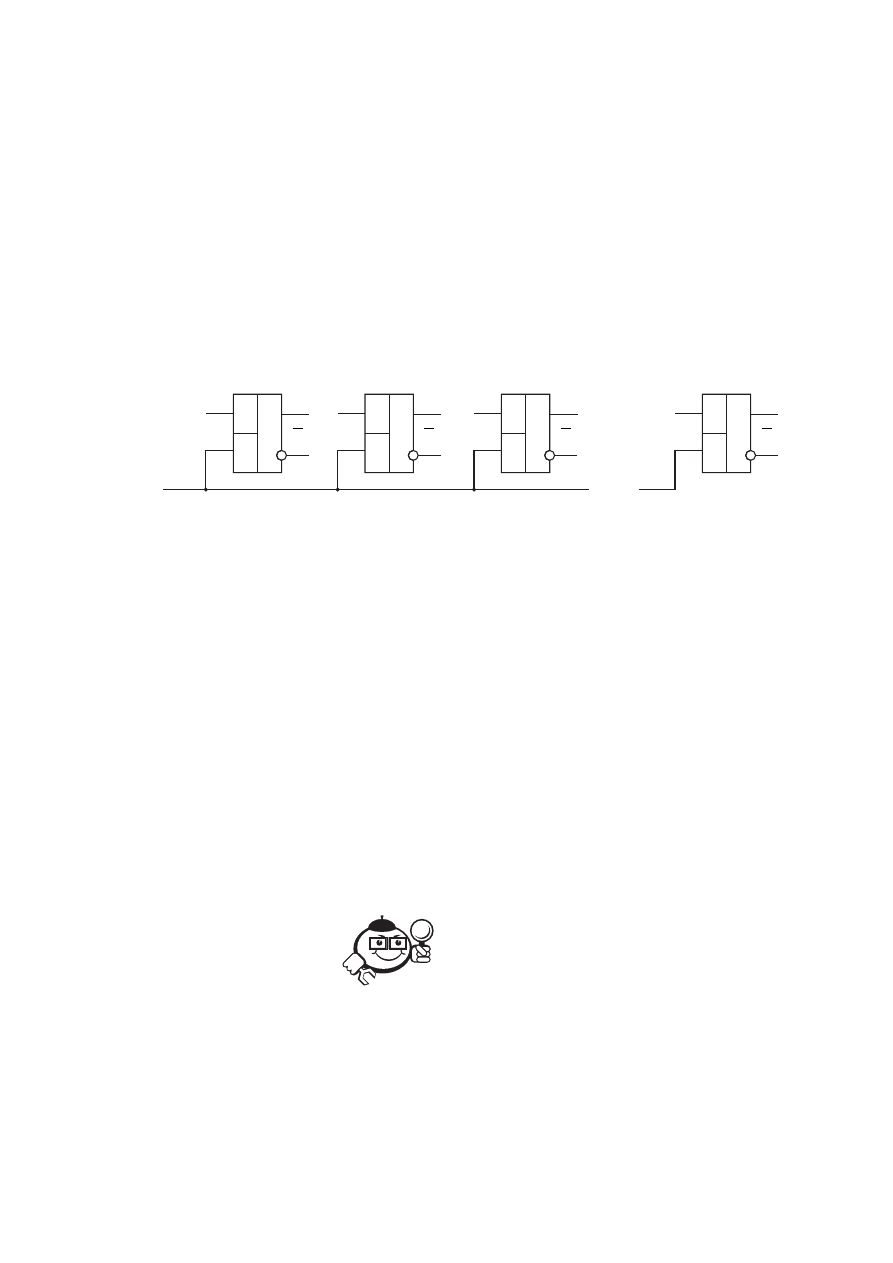
функций. Пример регистра приведён на рисунке 8.13. Всего в регистре n триг-
геров. Каждому триггеру поставлен в соответствие отдельный разряд n-
значного двоичного числа. Веса указаны над триггерами. Слева находится
старший разряд, справа – младший. Вес старшего разряда равен
1
2
−
n
, младше-
го –
0
2 = 1. В n-разрядном регистре может храниться одно число из
n
2 возмож-
ных.
Рис. 8.13
Чтобы регистр перевести в нулевое состояние, на вход «Установка нуля»
необходимо на время t подать низкий уровень сигнала. Обычно время t состав-
ляет доли микросекунды, но вообще на его продолжительность (в большую
сторону) ограничений нет. После этого в регистр можно записать любое n-
значное двоичное число подачей низкого уровня напряжения на единичные
входы соответствующих триггеров.
8.6 Построение комбинационных схем
Всякой булевой функции соответствует вполне определённая комбинаци-
онная схема. При построении комбинационных схем главной является операция
суперпозиции, согласно которой, как отмечено в п. 7.1, логические элементы
можно соединять последовательно. Рассмотрим несколько примеров.
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 8.1
· · · · · · · · · · · · · · · · · · · · · · ·
Реализовать в виде комбинационной схемы булеву функцию
.
D
ABC
f
+
=
Для её построения необходим один элемент И, описываемый функцией
,
ABC
ϕ =
и один двухвходовой элемент ИЛИ, реализующий функцию
ψ = Q + D.
S
n
A
R
A
n
T
Установка
нуля
2
0
S
3
A
R
A
3
T
S
2
A
R
A
2
T
S
1
A
R
A
1
T
2
n
1
–
2
n
1
–
2
n
1
–
. . .
. . .
. . .
174
Если в соответствии с операцией суперпозиции вместо переменной Q вы-
ражения ψ подставим функцию φ, то получим заданное выражение f. Физиче-
ски это соответствует подключению входа Q к выходу элемента φ, как показано
на рисунке 8.14. Схему можно представить и в более компактном виде
(рис. 8.15).
Рис. 8.14
Рис. 8.15
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 8.2
· · · · · · · · · · · · · · · · · · · · · · ·
Представить в виде комбинационной схемы функцию
.
)
)(
(
D
C
B
C
B
A
f
+
+
+
=
Эта функция представлена в КНФ. Для её реализации необходимо два
элемента ИЛИ и один элемент И. Схема приведена на рисунке 8.16. На рисун-
ке 8.17 она изображена в компактном виде.
Рис. 8.16
Рис. 8.17
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
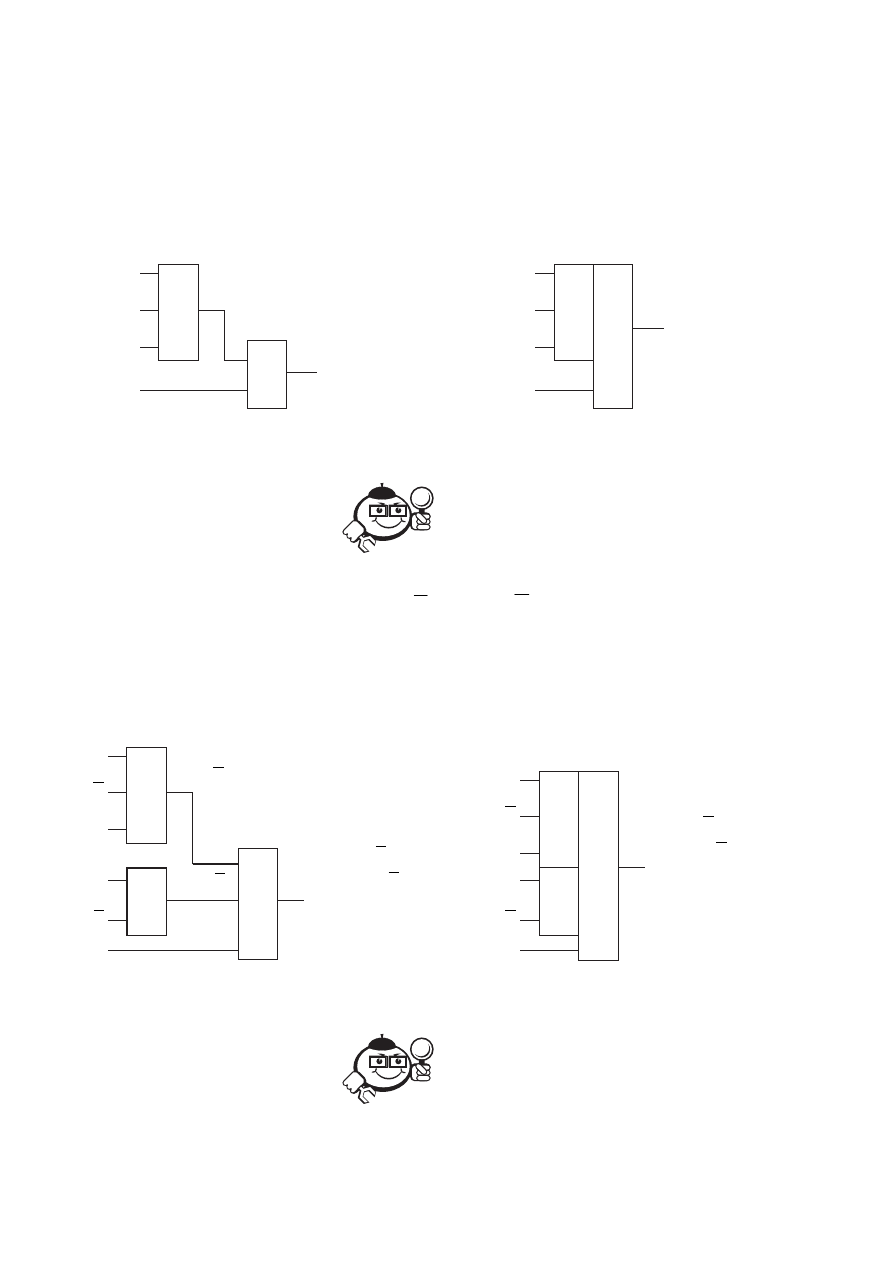
Пример 8.3
· · · · · · · · · · · · · · · · · · · · · · ·
В предыдущих двух примерах схемы построены на основе нормальных
форм. В данном же примере функция представлена в форме третьего порядка:
A
&
f = ABC+D
B
C
D
1
ABC
A
&
f = ABC+D
B
C
D
1
B
A
1
C
D
A
B
C
+
+
1
C
B
&
B
C
+
(
) &
f
A
B
C
=
+
+
&(
)
B
C D
+
B
A
1
C
D
1
C
B
(
) &
f
A
B
C
=
+
+
&(
)
B
C D
+
&
175
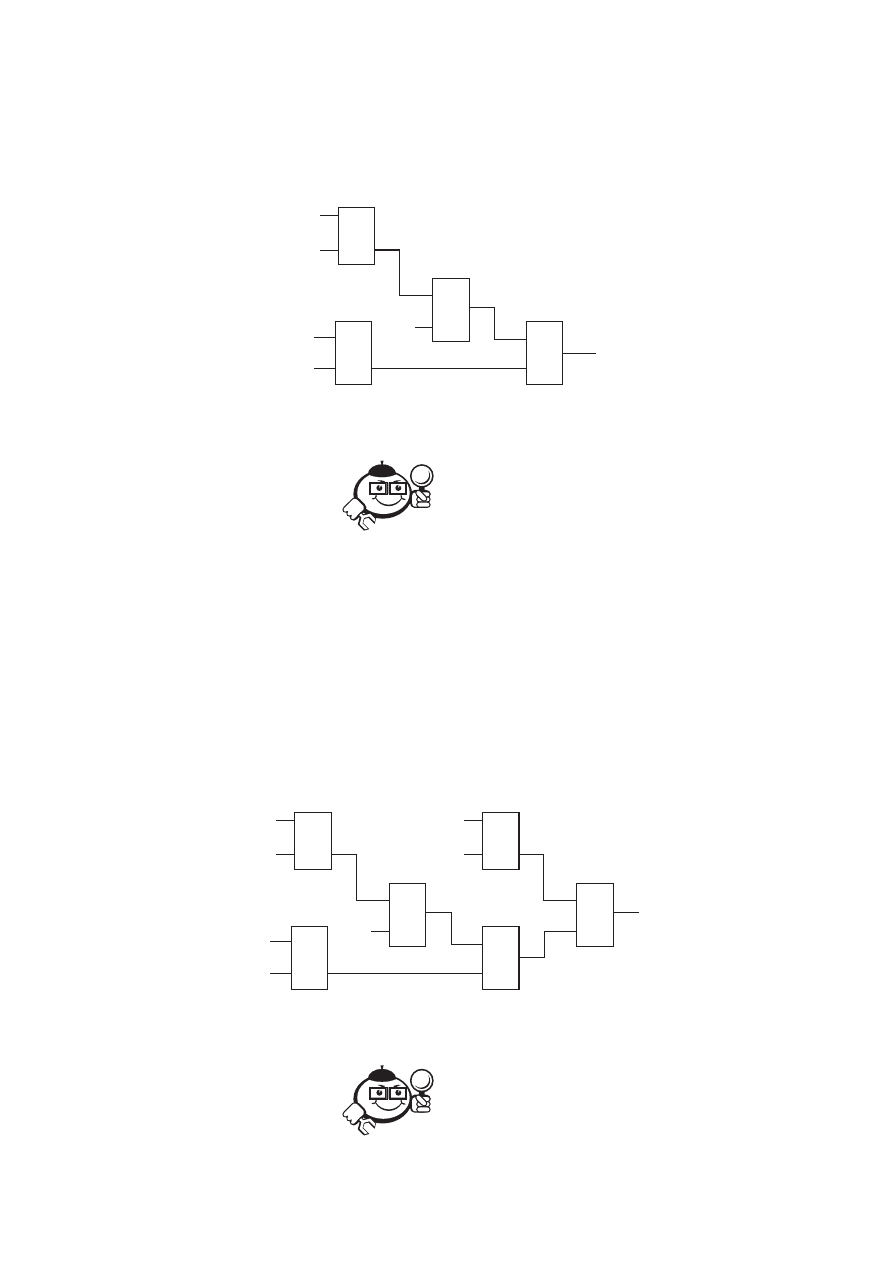
).
)(
(
B
A
R
PQ
f
+
+
=
Схема приведена на рисунке 8.18. Строится она по аналогии с предыду-
щими схемами.
Рис. 8.18
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 8.4
· · · · · · · · · · · · · · · · · · · · · · ·
Усложним функцию до формы четвёртого порядка:
.
)
)(
(
CD
B
A
R
PQ
f
+
+
+
=
Это выражение отличается от функции из примера 8.3, записанной в
форме третьего порядка, только тем, что в неё при помощи операции дизъюнк-
ции включена конъюнкция CD. Вследствие этого порядок функции повысился
до четвёртого. Соответственно и схема данного примера, изображённая на ри-
сунке 8.19, отличается от рисунка 8.18 лишь одной схемой И, реализующей
конъюнкцию CD.
Рис. 8.19
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 8.5
· · · · · · · · · · · · · · · · · · · · · · ·
Изобразить комбинационную схему согласно функции
&
PQ
PQ
R
+
A +B
P
Q
1
R
1
A
B
&
f
&
PQ
PQ
R
+
A +B
P
Q
1
R
1
A
B
&
f
&
CD
C
D
1