ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16656
Скачиваний: 202
176
.
)
](
)
)(
[(
PQ
K
DE
D
C
B
CD
B
A
f
+
+
+
+
+
+
=
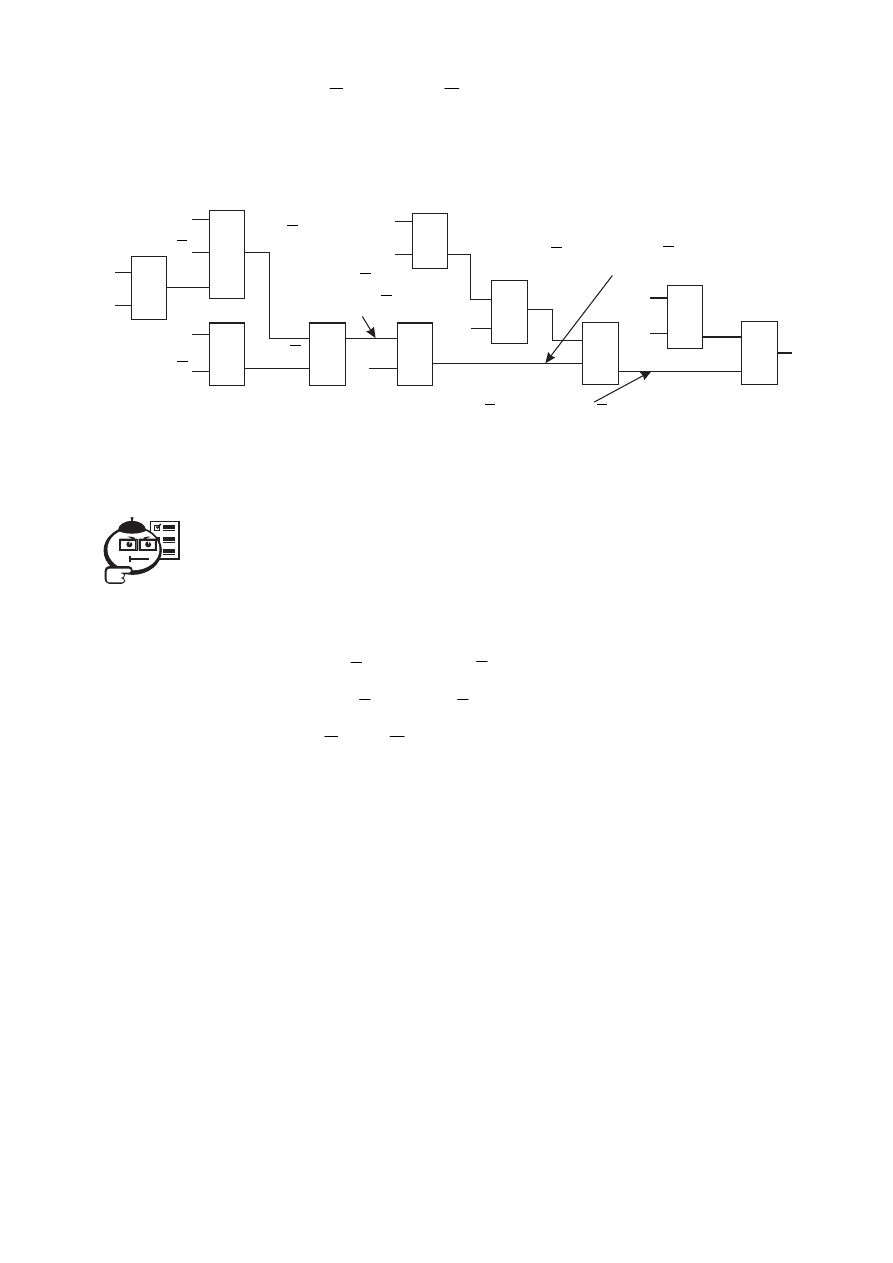
Это выражение шестого порядка. Схема строится по аналогии с преды-
дущими примерами (рис. 8.20).
Рис. 8.20
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Сколько трёхвходовых элементов И и трёхвходовых эле-
ментов ИЛИ потребуется для реализации следующих булевых
функций?
1)
1
(
)(
);
f
A
B
CDE B
C
=
+ +
+
2)
2
[(
)(
)
;
f
A
B
C B
C
E
F
PQR T
=
+ +
+ + +
+
+
3)
].
)
(
[
3
S
T
R
Q
P
F
E
D
C
B
C
B
A
f
+
+
+
+
+
+
=
2. Сколько всего элементов ИЛИ и сколько элементов
И содержится в схеме, построенной по минимальной ДНФ функ-
ции f
1
предыдущего примера?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
8.7 О весовых и невесовых кодах
Пусть дано двоичное число, например 11010. Какое десятичное число ему
соответствует? В общем случае однозначно ответить на этот вопрос невозмож-
но. Если двоичный код является невесовым, то необходима таблица, где для
каждого кода указано соответствующее десятичное число. Соответствие может
быть задано не только таблицей, но и какими-либо формулами или правилами.
В весовых системах таблицы не требуются. Перевод двоичных кодов
в десятичную систему осуществляется на основе полинома вида
f
1
&
P
Q
PQ
&
1
1
&
1
&
D
E
DE
K
B
1
&
C
D
A
B
CD
+
+
DE+K
D
A
B
C
+
(
) &
f
A
B
CD
=
+
+
&(
)
B
C
+
(
)(
)
A
B
CD B
C
D
+
+
+
+
[(
)(
)
](
)
A
B
CD B
C
D DE
K
+
+
+
+
+
B
C

177
,
0
0
1
1
2
2
1
1
q
a
q
a
q
a
q
a
N
n
n
n
n
+
+
+
+
=
−
−
−
−
…
где коэффициенты
0
2
1
,
,
,
a
a
a
n
n
…
−
−
изображают цифры; n – длина кода, т. е. чис-
ло входящих в него знаков 0 или 1. Числа
0
1
2
1
,
,
,
,
q
q
q
q
n
n
…
−
−
обозначают веса.
Именно этими весами и обусловлено все многообразие способов двоичного ко-
дирования чисел, представленных в других системах счисления.
Самым распространенным весовым двоичным кодом является код, по-
строенный на двоичной системе счисления с весами, равными степени числа 2:
1, 2, 4, 8, 16, 32, ….
Например, если n = 5, то
.
1
,
2
,
4
,
8
,
16
0
1
2
3
4
=
=
=
=
=
q
q
q
q
q
Тогда коду 11010 соответствует десятичное число:
1⋅16 + 1⋅8 + 0⋅4 + 1⋅2 + 0⋅1 = 26.
При других весах тому же коду 11010 может соответствовать другое де-
сятичное число. Например, если
.
5
,
1
,
1
,
3
,
12
0
1
2
3
4
=
=
=
=
=
q
q
q
q
q
то двоичному коду 11010 соответствует число 16, так как
1⋅12 + 1⋅3 + 0⋅1 + 1⋅1 + 0⋅5 = 16.
Весовой код задают обычно упорядоченной последовательностью весов.
Например, если
4
3
2
1
0
4,
1,
1,
1,
4,
q
q
q
q
q
=
=
=
=
=
то можно записать только веса: 41114, откуда видно, что код пятизначный и что
веса левого и правого разрядов равны 4, а остальные равны 1. Этого вполне до-
статочно, чтобы по коду найти его десятичный эквивалент. Например, двоич-
ному коду 11010 в системе 41114 соответствует десятичное число 6:
1⋅4 + 1⋅1 + 0⋅1 + 1⋅1 + 0⋅4 = 6.
Таким образом, чтобы по записи весового двоичного кода найти его деся-
тичный эквивалент, необходимо знать веса двоичных разрядов. На практике
обычно считается, что если веса не указаны, то они представляют собой степе-
ни числа 2. Примером может служить код 8421, где веса равны:
.
2
1
,
2
2
,
2
4
,
2
8
0
1
2
3
=
=
=
=
Во всех же остальных случаях необходимо указывать, в какой системе ве-
сов записываются двоичные коды.

178
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 8.6
· · · · · · · · · · · · · · · · · · · · · · ·
Пусть задан весовой двоичный код P = 1224. В нём четыре знака. Всего
четырёхзначных кодов возможно 16. Но сумма весов в коде 1224 равна 9. Сле-
довательно, закодировать этим кодом можно только 10 каких-либо объектов.
Пусть это будут десятичные цифры. Очевидно, что некоторые цифры могут
быть закодированы неоднозначно, т. е. различными двоичными кодами:
0 – 0000;
3 – 1100, 1010; 6 – 0011, 0101;
1 – 1000;
4 – 0110, 0001; 7 – 1011, 1101;
2 – 0100, 0010; 5 – 1110, 1001; 8 – 0111,
9 – 1111.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 8.7
· · · · · · · · · · · · · · · · · · · · · · ·
Пусть задан пятизначный двоичный весовой код Q = 11115. Так как сум-
ма весов равна 9, то его также можно использовать для кодирования десятич-
ных цифр. Существует 32 последовательности нулей и единиц по пять знаков
каждая. Но для кодирования десятичных цифр используется только 10 из них.
Это значит, что избыточность пятизначного кода при кодировании десятичных
цифр гораздо больше по сравнению с четырёхзначными кодами. Список деся-
тичных цифр и способов их кодирования в системе 11115 имеет вид:
0 – 00000;
1 – 10000, 01000, 00100, 00010;
2 – 11000, 10100, 10010, 01100, 01010, 00110;
3 – 11100, 11010, 10110, 01110;
4 – 11110;
5 – 00001;
6 – 10001, 01001, 00101, 00011;
7 – 11001, 10101, 10011, 01101, 01011, 00111;
8 – 11101, 11011, 10111, 01111;
9 – 11111.
Согласно этому списку цифры 0, 4, 5 и 9 кодируются однозначно. Циф-
рам 1, 3, 6 и 8 соответствует по четыре кода. Самыми «урожайными» с позиций
избыточности кодов являются цифры 2 и 7. Каждую их них можно закодиро-
вать шестью способами.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·

179
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1. Сколько возможно способов кодирования в системе 112231
цифры 3? 5?
2. Сколько возможно способов кодирования в системе 111141
цифры 4? 6?
3. Какие десятичные цифры невозможно закодировать в си-
стеме 1356?
4. Какие десятичные цифры можно закодировать двумя спо-
собами в системе двоичных кодов 1356?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
8.8 Синтез преобразователя весового двоичного кода
В предыдущем параграфе приведены коды P = 8421 и Q = 11115. На их
основе построим комбинационный преобразователь входного кода P в выход-
ной код Q.
Сначала построим таблицу (табл. 8.1). В ней три области: левая, средняя и
правая. В средней области, там, где колонки обозначены буквами A, B, C, D (это
выходы триггеров), размещены входные коды с весами 8421. Справа в виде пя-
ти колонок, обозначенных символами f
1
, f
2
, f
3
, f
4
, f
5
, расположены выходные
двоичные коды с весами 11115, обозначающие те же десятичные цифры, что и в
области входных кодов. Веса в таблице не указаны, но они подразумеваются.
В левой части таблицы приведена колонка, где записаны десятичные эквива-
ленты входных кодов.
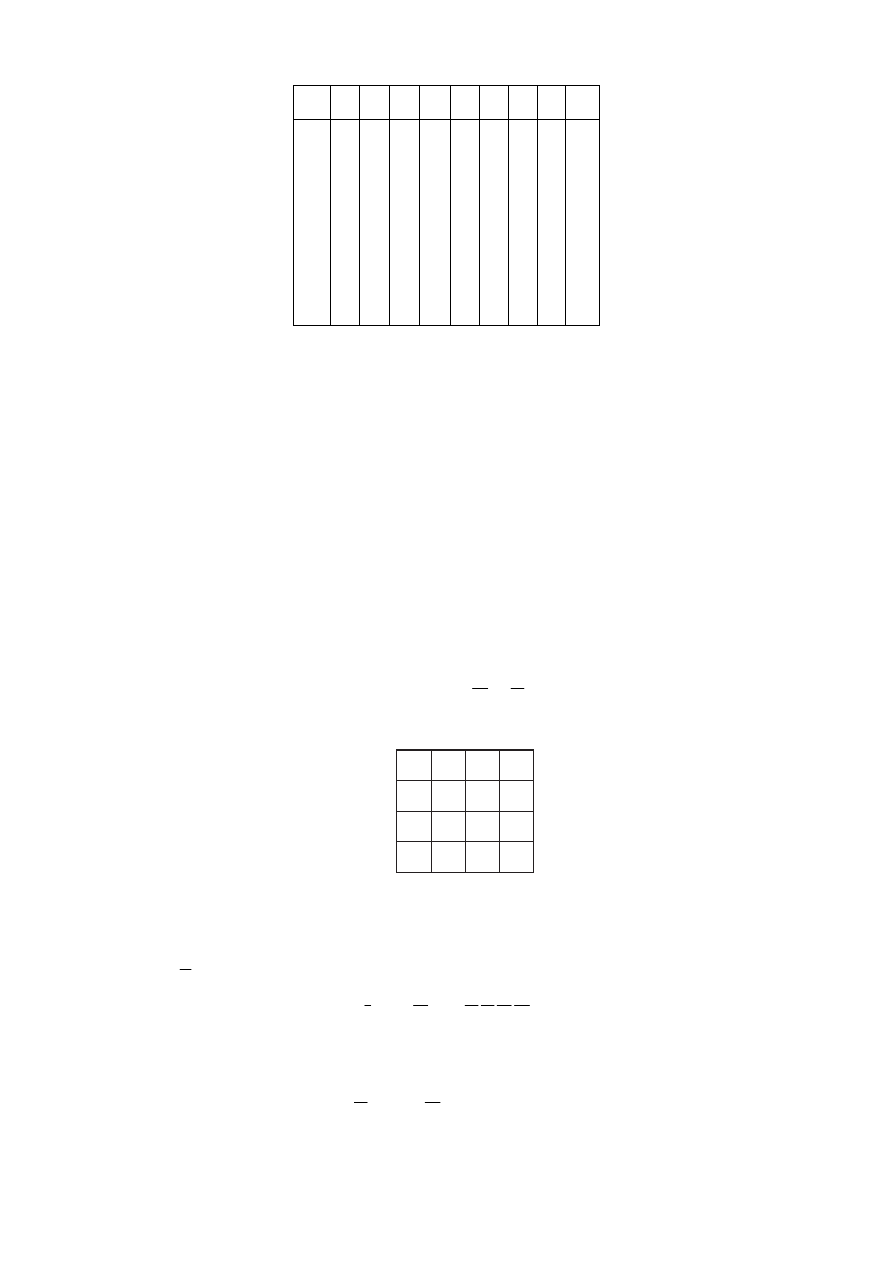
Таблица 8.1
A B C D f
1
f
2
f
3
f
4
f
5
0
1
2
3
4
5
6
7
8
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
1
1
1
0
1
1
1
0
0
1
1
1
0
0
1
1
0
0
0
1
1
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
1
1
1
180
A B C D f
1
f
2
f
3
f
4
f
5
9
10
11
12
13
14
15
1
1
1
1
1
1
1
0
0
0
1
1
1
1
0
1
1
0
0
1
1
1
0
1
0
1
0
1
1
×
×
×
×
×
×
1
×
×
×
×
×
×
1
×
×
×
×
×
×
1
×
×
×
×
×
×
1
×
×
×
×
×
×
В правой части таблицы 8.1 кроме нулей и единиц имеются крестики.
Ими обозначены «лишние» входные двоичные коды, которым не соответствует
никакой выходной код, так как кодов в системе 11115 существует только 10.
«Лишние» коды на вход преобразователя подаваться не будут, следовательно,
их можно рассматривать как неопределённые состояния. Таблица 8.1 представ-
ляет собой таблицу истинности для пяти булевых функций, найдем их мини-
мальные ДНФ и КНФ.
Минимизируем функцию f
1
:
f
1
= (1, 2, 3, 4, 6, 7, 8, 9); [10, 11, 12, 13, 14, 15].
Карта Вейча приведена на рисунке 8.21 (расположение букв вокруг кар-
ты, как в разделе 5). Минимальная ДНФ, согласно этой карте, имеет вид
.
1
D
B
D
B
C
A
f
+
+
+
=
Рис. 8.21
Находим минимальную КНФ. По карте Вейча (рис. 8.22) минимизируем
функцию
1
:
f
.
1
D
C
B
A
D
C
B
f
+
=
Инвертируем это выражение по теореме де Моргана и получаем искомую
КНФ:
).
)(
(
1
D
C
B
A
D
C
B
f
+
+
+
+
+
=
f
1
1
=
1
1
1
1
1
1
1
×
×
×
×
×
×