ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7083
Скачиваний: 35
3.2 Венгерский алгоритм нахождения
максимального паросочетания в двудольном графе
51
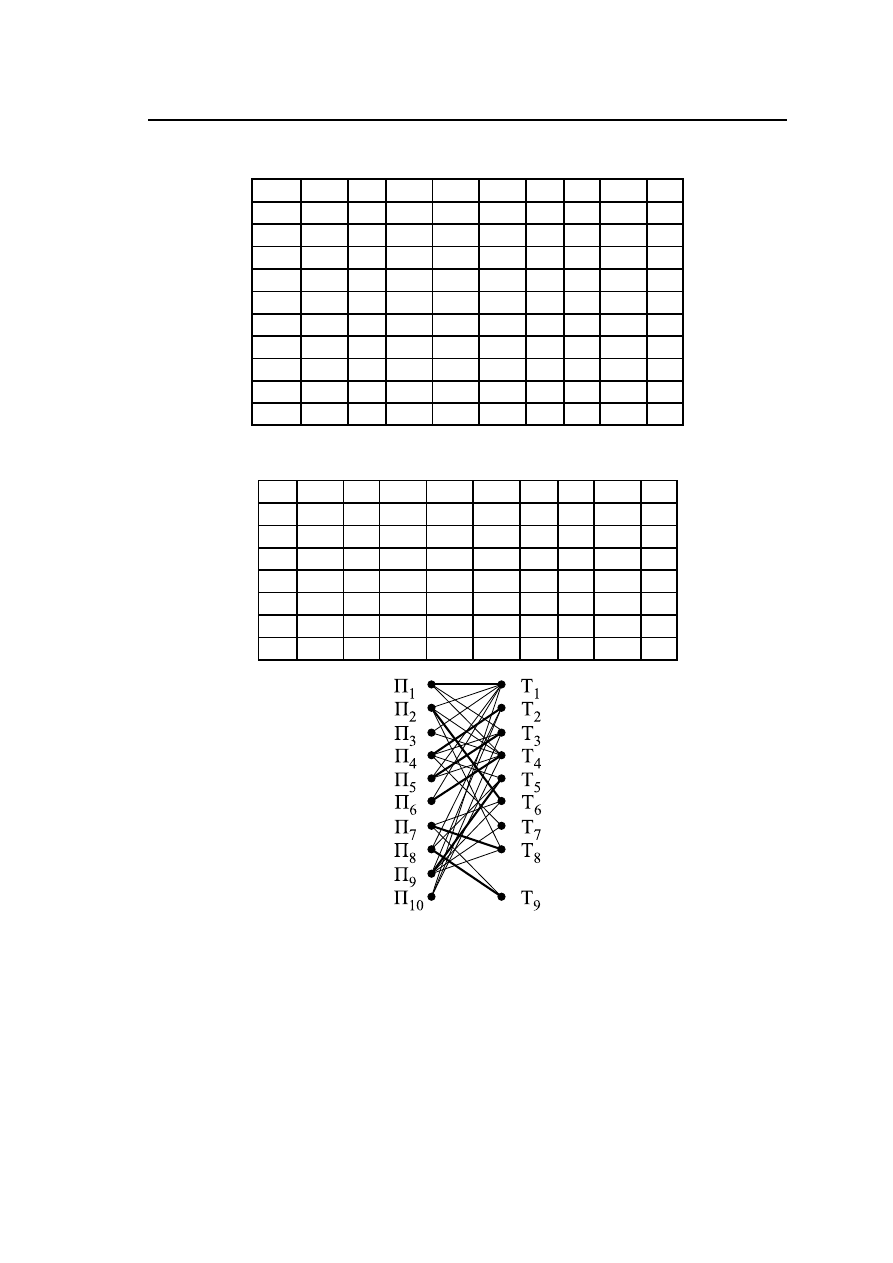
Таблица 3.2 – Матрица смежности B графа L
Т
1
+
Т
*
2
Т
3
+
Т
4
+
Т
5
+
Т
*
6
Т
7
Т
8
+
Т
9
П
1
+
1+
1−
1
П
2
+
1
1−
1
1+
П
3
+
1−
1+
П
*
4
1
1+
1
1
П
5
1
1
1
П
6
1
1
П
7
+
1+
1−
1
П
8
+
1+
1−
1
П
9
+
1
1+
1−
1
1
П
10
1
1
Таблица 3.3 – Матрица смежности B графа L
B
Т
1
+
Т
*
2
Т
3
+
Т
4
+
Т
5
+
Т
*
6
Т
7
Т
8
+
Т
9
П
1
1+
1−
1
П
2
1
1−
1+
1
П
3
1
1
П
4
1
1
1
1
П
*
5
1
1+
1
П
6
1−
1+
П
7
1−
1+
1
Рис. 3.2 – Наибольшее паросочетание K
ν
, выделенное в двудольном
графе L
=
(X
1
, X
2
, U
)
Из матрицы B (табл. 3.3) видно, что увеличить тонкую чередующуюся цепь Q
нельзя, но в графе остались ненасыщенные вершины, инцидентные одному и тому
же ребру, которые можно добавить к искомому паросочетанию K
ν
.
Это рёбра (П
8
, Т
9
), (П
4
, Т
2
).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

52
Глава 3. Экстремальные задачи на графах
. . . . . . . . . . . . . . . . . . . . . . . . .
Выводы
. . . . . . . . . . . . . . . . . . . . . . . . .
В результате получаем наибольшее паросочетание K
ν
(рис. 3.2), в которое вхо-
дят рёбра:
(П
5
, Т
3
),(П
1
, Т
1
),(П
6
, Т
4
),(П
2
, Т
6
),(П
7
, Т
8
),(П
9
, Т
5
),(П
8
, Т
9
),(П
4
, Т
2
).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
На рисунке 3.2 рёбра искомого наибольшего паросочетания K
ν
обозначены
жирными линиями.
3.3 Оптимальные потоки
в транспортных/информационных сетях
Теория транспортных и информационных сетей возникла при решении задач,
связанных с организацией перевозки грузов и передачей информации. Тем не ме-
нее понятие потока на транспортной сети и алгоритм нахождения потока наиболь-
шей величины, критерий существования потока, насыщающего выходные дуги се-
ти, оказались плодотворными для многих других прикладных и теоретических во-
просов комбинаторного характера.
Введём основные понятия теории.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Cетью называется ориентированный связный граф G
=
(V,U),
в котором отсутствуют петли и существует одна и только одна
вершина v
0
∈ V, такая, что множество Г
−1
v
0
= ∅, т. е. степень захода
вершины v
0
равна 0, и существует одна и только одна вершина
z
∈ V, такая, что множество Гz = ∅, т. е. степень исхода вершины
z равна 0. Вершина v
0
называется истоком (вход) сети, вершина z
называется — стоком (выход) сети.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Каждой дуге u
∈ U сети сопоставлено целое положительное число c
(u), кото-
рое называется пропускной способностью дуги.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Пусть U
−
v
— множество дуг, заходящих в вершину v, а U
+
v
— множе-
ство дуг, выходящих из вершины v. Целочисленная неотрицатель-
ная функция
3
(u), определенная на множестве U дуг графа G,
называется потоком, если она удовлетворяет следующим требо-
ваниям:
∑
u
∈U
−
v
3
(u) = ∑
u
∈U
+
v
3
(u) (v /= v
0
, v
/= z),
для всех v
∈ V
/{v
0
, z
}; для всех u ∈ U.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.3 Оптимальные потоки в транспортных/информационных сетях
53
Задача о максимальном потоке.
Группу задач топологического анализа составляют задачи на распределение
сетевых потоков. Это задача о максимальном потоке, в содержание которой оказы-
ваются взаимосвязанными топология сети, пропускные способности каналов свя-
зи или транспортных коммуникаций и распределение сетевых потоков. Подбирая
определенным образом значение сетевых потоков и исходя из заданного распреде-
ления пропускных способностей каналов, можно получить единственно возмож-
ное максимальное для заданной топологии значение общего суммарного потока
в сети. В этом случае, очевидно, ресурсы сетевой связи используются наиболее
полно и эффективно.
Задача о максимальном потоке формулируется следующим образом: пусть за-
дано исходное распределение потоков по дугам графа, отображающего топологи-
ческую структуру сети, а также пропускные способности дуг. Необходимо найти
максимально возможное для данной сети значение суммарного потока между ис-
точниками и стоками, т. е. определить, как увеличить поток, если он не достиг
этого значения. Применительно к рассматриваемой задаче используется одно из
важных положений теории потоков, которое сформулировано и доказано в виде
теоремы Фордом и Фалкерсоном. Согласно этой теореме максимально возможное
значение суммарного потока на конечных дугах равно минимальной пропускной
способности выбранного разреза. При этом под пропускной способностью разреза
понимается сумма пропускных способностей дуг, образующих разрез.
В символической форме записи соотношение, отражающее содержание теоре-
мы Форда—Фалкерсона, выглядит следующим образом:
∑
i
∈B
∑
j
∈̃
B
3
(v
i
, v
j
) = ∑
i
∈B
∑
j
∈̃
B
c
(v
i
, v
j
),
где
3
(v
i
, v
j
) — значение потока по дугам заданного графа; c(v
i
, v
j
) — пропускная спо-
собность дуги; B — множество вершин подграфа, образующих разрез; ̃
B — дополне-
ние множества B до множества V .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Множество B вершин подграфа, образующих разрез всегда содер-
жит вершину z (сток) и никогда не содержит вершину v
0
(исток).
Разрез R
(G) сети включает множество дуг U
′
⊂ U сети, исходящих
из вершин множества ̃
B и входящих в вершины множества B.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Доказательство теоремы Форда—Фалкерсона строится методом от противно-
го на следующих предположениях: граф имеет две характерные вершины — исток
и сток, а разрез R
(G) вершины графа делит на два взаимодополняющих множе-
ства B и ̃
B.
Допустим, что на графе задан максимальный поток Ф, а сток z не отделен
от множества вершин B разрезом, т. е. z
∈ B. Тогда из определения разреза и при
данном условии следует, что существует хотя бы один путь из истока v
0
в сток —
вершину z, для которого должны выполняться условия:
• для прямых дуг пути
(v
0
−
z
) ∶ — 3(v
i
, v
j
) < c(v
i
, v
j
);
• для обратных дуг пути
(v
0
−
z
) ∶ — 3(v
i
, v
j
) > 0.

54
Глава 3. Экстремальные задачи на графах
Это свидетельствует о том, что поток на сети не является максимальным и его
величину можно увеличить, насыщая отдельные дуги по путям, идущим от истока
к стоку.
Иначе, если задан разрез, то он своими дугами однозначно определяет макси-
мально возможный, проходящий через них поток. Очевидно, разрез
(v
0
−
z
) ми-
нимальной общей пропускной способностью дуг задает максимально возможный
для данного графа поток от истока v
0
к стоку z.
Алгоритм Форда—Фалкерсона.
Для транспортной/информационной сети важно найти такие минимальные раз-
резы и оценить соответствующие им значения максимального потока. Это можно
осуществить с помощью алгоритма Форда—Фалкерсона.
Принцип, лежащий в основе алгоритма Форда—Фалкерсона, заключается в том,
чтобы найти все возможные насыщенные пути (цепи), ведущие от v
0
к z.
С этой целью последовательно, начиная с вершины x
0
, просматриваются сна-
чала все смежные ей
{v
i
} вершины. Из множества дуг {(v
0
, v
i
)}, соединяющих v
0
с
{v
i
}, выбирают одну, у которой значение потока ближе всех подходит к значению
насыщения. Помечают вершину v
i
знаком, показывающим, что она была просмот-
рена, и приписывают ей величину
δ, на которую можно увеличить поток по дуге,
ведущей в эту вершину. Затем просматривают все последующие смежные с v
i
вер-
шины
{v
j
} и останавливаются на той, в которую ведёт дуга с потоком, ближайшим
к значению насыщения. По этой дуге переходят в соответствующую вершину v
j
.
Делают пометки вершин и идут далее в направлении вершины z. Если путь, на
котором будут отмечены все пройденные вершины, приведёт в вершину z, то это
говорит о том, что найден один из путей, наиболее близкий к насыщению. Нуж-
но довести поток по нему до насыщения, увеличивая тем самым поток на графе.
Значение, на которое можно увеличить поток, находится как минимальное
δ из
множества отмеченных значений в пройденных по данному пути вершинах. Для
выяснения вопроса, является ли полученный таким образом поток максимальным
или нет, необходимо просмотреть все другие возможные пути, ведущие от x
0
к z.
Для этого необходимо возвратиться в x
0
и повторить описанные выше действия,
но идти следует по еще не помеченным вершинам. В результате выполнения этих
действий можно столкнуться с двумя вариантами:
1) пройденный путь снова приводит от x
0
к z, т. е. удается найти ненасыщен-
ные пути и, значит, можно увеличить потоки на их дугах;
2) придя в некоторую вершину, обнаружить, что все смежные с ней вершины
помечены и, следовательно, больше путей, ведущих к z, нет. Это указывает
на то, что на сети G получен максимальный поток.
Согласно теореме Форда и Фалкерсона значение полученного максимального
потока можно вычислить, выделив дуги разреза R
(G) с минимальной пропускной
способностью и просуммировав их пропускные способности.
3.3 Оптимальные потоки в транспортных/информационных сетях
55
. . . . . . . . . . . . . . . . . . . . . .
Пример 3.2
. . . . . . . . . . . . . . . . . . . . .
Пример решения задачи о максимальном потоке с помощью алгоритма
Форда—Фалкерсона
Пусть задана сеть G
=
(X,U) (рис. 3.3), на дугах u
ij
которой в скобках обозна-
чены значения пропускных способностей дуг — c
(u).
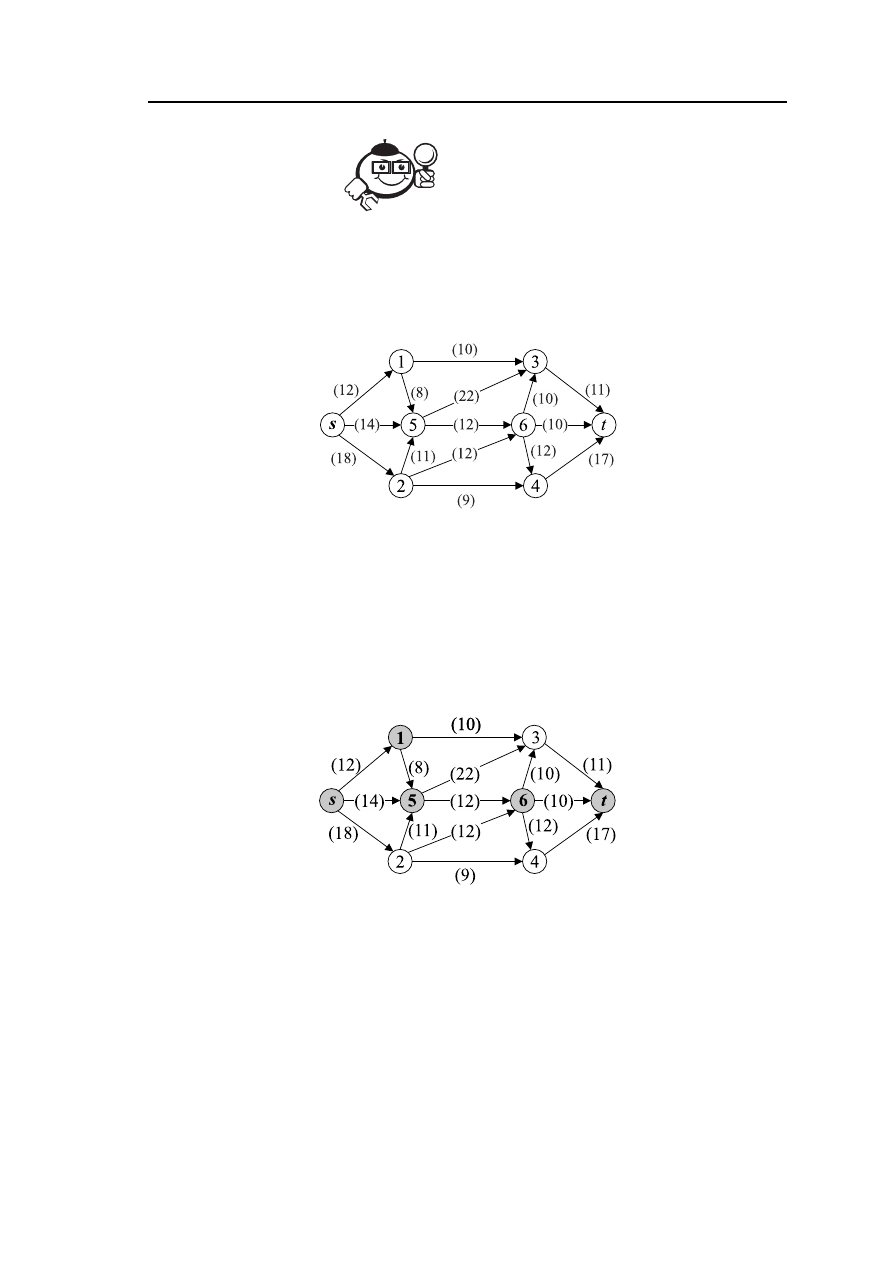
Рис. 3.3 – Сеть G
1. Зададим на сети нулевой поток (на всех дугах величина потока
3
ij
рав-
на 0). Нулевой поток — это начальный допустимый поток на сети. Значение потока
на каждой дуге u
ij
будем указывать за скобками пропускной способности дуги:
c
(u
ij
)3(u
ij
). Значение потока, равное «0», не указываем.
2. Выбираем на сети (произвольно) путь, ведущий из вершины s в вершину t:
s
→ 1 → 5 → 6 → t (рис. 3.4).
Рис. 3.4 – Сеть G
3. Вычисляем значения
{δ
ij
= c
(u
ij
) − 3(u
ij
)} на каждой дуге пути: s → 1 →
→ 5 → 6 → t и выбираем минимальное из них. minδ
ij
= 8 (так как 3
(u
ij
) = 0 на всех
дугах данного пути). На величину min
δ
ij
= 8 увеличиваем поток на каждой дуге
пути s
→ 1 → 5 → 6 → t. Дуга (1,5) становится «насыщенной», так как поток на ней
стал равен 8 (рис. 3.5).
4. Выбираем следующий путь, ведущий из s в t: s
→ 1 → 3 → t (рис. 3.6),
и для него вычисляем значение min
δ
ij
(аналогично тому, как это делалось в п. 3).
min
δ
ij
= 4.