ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7080
Скачиваний: 35

2.9 Структурный анализ графов
41
1. Упорядочим полученные множества вершин в порядке убывания их карди-
нальных чисел: x
2
x
4
x
5
x
7
; x
1
x
3
x
6
x
8
; x
4
x
8
; x
2
x
6
; x
3
x
7
; x
1
x
5
.
2. Припишем вершинам множества
(x
2
, x
4
, x
5
, x
7
) цвет «1» (цвет выбирается
произвольно).
3. Удалим раскрашенные вершины из всех множеств и оставшиеся множества
упорядочим в порядке убывания их мощности:
(x
1
, x
3
, x
6
, x
8
); x
8
; x
6
; x
3
; x
1
.
4. Припишем вершинам множества x
1
, x
3
, x
6
, x
8
цвет «2».
5. Удалим раскрашенные вершины из всех множеств.
Получаем пустое множество.
Вывод. Это говорит о том, что все вершины графа G — раскрашены. Для рас-
краски потребовалось всего два цвета, т. е. хроматическое число
γ
(G) графа G
равно двум:
γ
(G) = 2.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.9.2 Компоненты связности графа
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Граф G
(X,U) связен, если любые его две вершины можно соеди-
нить простой цепью.
Подграф G
′
графа G называется компонентой связности гра-
фа G, если:
1) подграф G
′
связен;
2) подграф G
′
обладает свойством максимальности, т. е. если
G
′′
— некоторый другой связный подграф графа G и G
′
⊂
⊂ G
′′
, то графы G
′
и G
′′
совпадают.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Иными словами, компонента связности — это наибольший связный
подграф данного графа.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
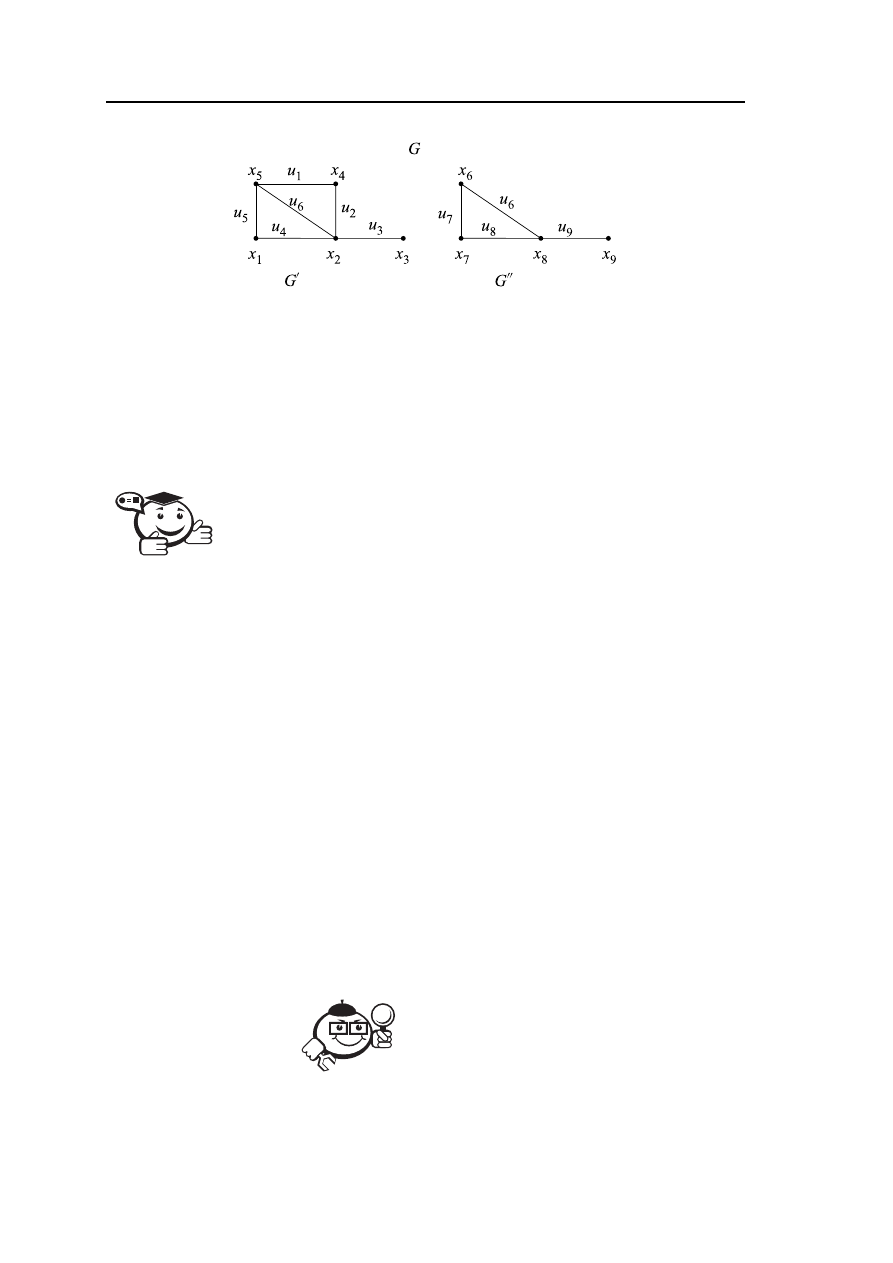
Пример 2.15
. . . . . . . . . . . . . . . . . . . . .
Граф G
=
(X,U) (рис. 2.24) содержит две компоненты связности: G
′
с верши-
нами
(x
1
, x
2
, x
3
, x
4
, x
5
) и G
′′
с вершинами
(x
6
, x
7
, x
8
, x
9
).
42
Глава 2. Теория графов
Рис. 2.24 – Граф G содержит две компоненты связи: G
′
и G
′′
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Способ определения числа компонент связности графа.
При помощи матрицы смежности графа G можно определить число компонент
связности данного графа. Для этого определим операцию элементарной склейки
вершин в мультиграфе и выясним, как эта операция преобразует матрицу смежности.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Мультиграф G
′
=
(X
′
, U
′
) можно получить из мультиграфа G =
=
(X,U) при помощи пошагового выполнения операции элемен-
тарной склейки вершин x
i
и x
j
из множества X , если:
1) X
′
=
(X/({x
i
} ∪ {x
j
})) ∪ {z}, где z /∈ X;
2)
(x
m
, x
l
, n
) ∈ U
′
, где
(m,l /= i,j), n — номер ребра (x
m
, x
l
),
тогда и только тогда, когда
((x
m
, x
l
),n) ∈ U, и (x
m
, z, n
) ∈ U
′
,
где
(m /= i,j).
Здесь z — «новая» вершина G
′
, полученная от склеивания вершин
в графе G.
Из условий 1, 2 следует, что склеиваются только те пары вершин,
которые являются концами одного и того же ребра. Ориентация
рёбер на операцию склеивания не влияет.
Очевидно, что после каждого выполнения операции «склеивания»
количество вершин множества X
′
уменьшается на единицу, а ко-
личество рёбер и их идентификационные номера остаются неиз-
менными, т.е.
∣U
′
∣ = ∣U∣.
Иными словами, при склейке вершин x
i
и x
j
склеиваются только
концы дуг, совпадающие с x
i
и x
j
, а сами дуги сохраняются.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
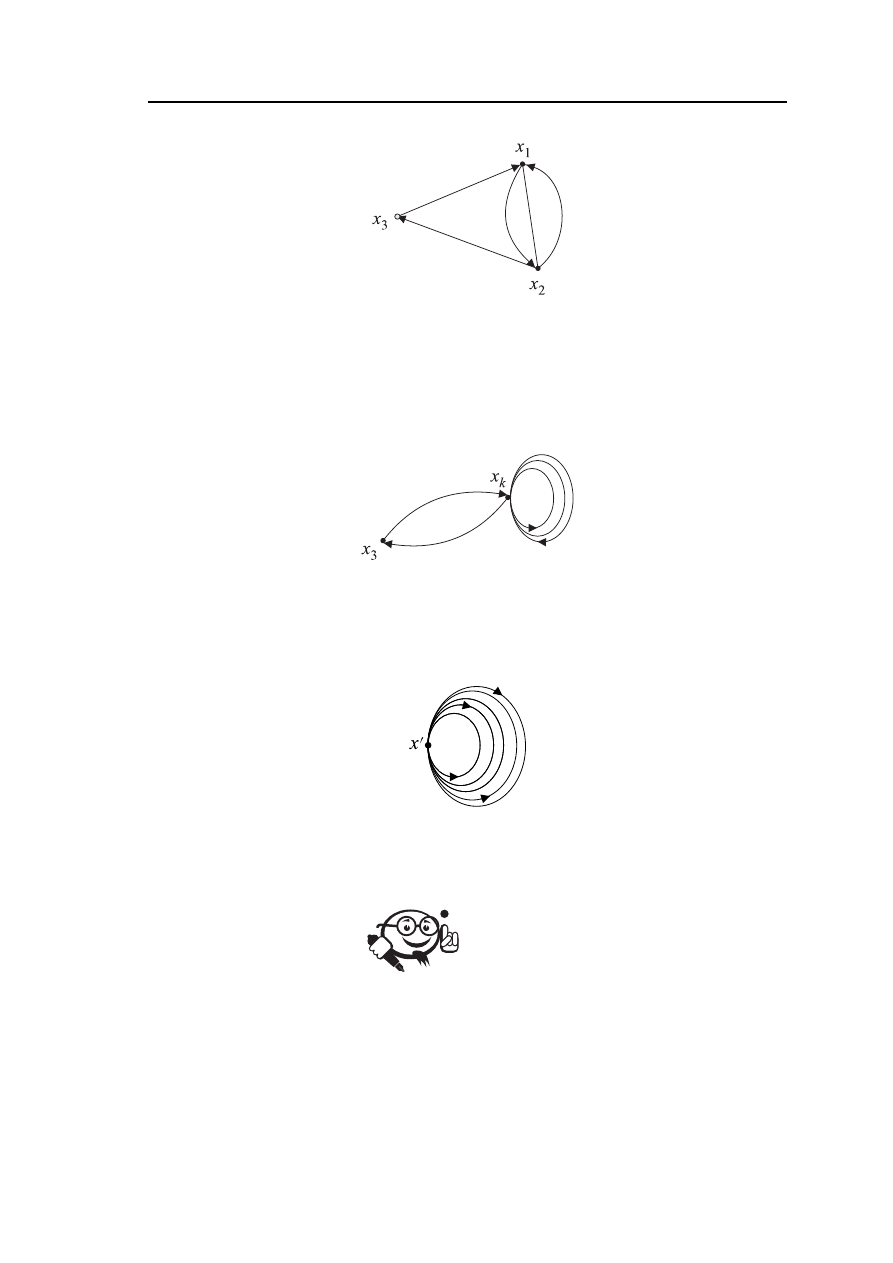
Пример 2.16
. . . . . . . . . . . . . . . . . . . . .
В графе G (рис. 2.25) поэтапно выполнить операцию склеивания вершин.
2.9 Структурный анализ графов
43
Рис. 2.25 – Граф G
Решение:
1-этап. В графе G склеиваем вершины x
1
и x
2
. Получаем граф G
′
(рис. 2.26),
где вершина x
k
= x
1
+
x
2
.
Рис. 2.26 – Граф G
′
, полученный из графа G склеиванием вершин x
1
и x
2
2-этап. В графе G
′
склеиваем вершины x
3
и x
k
. Получаем граф G
′′
(рис. 2.27),
где вершина x
′
= x
3
+
x
k
.
Рис. 2.27 – Граф G
′′
получен из графа G
′
склеиванием вершин x
3
и x
k
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
Выводы
. . . . . . . . . . . . . . . . . . . . . . . . .
Очевидно, поэтапное попарное склеивание вершин графа, принадлежащих од-
ной и той же компоненте связности, не изменяет количества компонент связности.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Процедура склеивания вершин графа должна выполняться поэтапно для каж-
дой пары вершин, из множества тех вершин, к которым можно применять данную
процедуру. После каждого склеивания какой-либо пары вершин получается «но-
вый» граф, в котором нарушен естественный порядок нумерации вершин, в силу

44
Глава 2. Теория графов
того, что количество вершин в новом графе на одну меньше числа вершин в графе,
из которого он получен, и появляется вершина с неопределённым номером.
Для восстановления естественной нумерации графа можно применить следу-
ющий способ.
Обозначим
∣X∣ через n. Это число вершин графа G
(k)
, полученного на k-й ите-
рации склеивания вершин, где k
= 0, 1, . . ., t. Перенумеруем вершины графа G
′
,
полученного элементарной склейкой x
i
и x
j
, следующим способом.
Номера вершин, начиная с первого до i − 1, сохраняют свои значения. Номера
вершин, начиная с i + 1 до j − 1, уменьшают свои значения на единицу, номера
остальных вершин уменьшают значения на две единицы.
«Новой» вершине x
′
присваивается номер (n − 1).
Так вершины графа G
′
(рис. 2.26) получат следующие номера: вершина x
′
—
номер 2; вершина x
3
— номер 1. Единственная вершина x
′′
графа G
′′
(рис. 2.27)
получит номер «1».
Если исходный граф G
(X,U) задан матрицей смежности, то значения элемен-
тов матрицы смежности нового графа G
′′
, полученного в результате склеивания
какой-либо пары вершин из множества X , можно получить, выполняя следующие
вычисления.
Обозначим через f
(k) (k = 1,2,...,n − 2) старый номер вершины с новым но-
мером k. Тогда матрица
∣∣a
′
ijk
∣∣ нового графа строится по матрице ∣∣a
ij
∣∣ графа по
формулам:
a
′
lk
= a
f
(l)f (k)
(l,k ⩽ n − 2),
a
′
n
−1k
= a
if
(k)
+
a
lf
(k)
(k ⩽ n − 2),
a
′
l, n
−1
= a
f
(l)i
+
a
f
(l)j
(l ⩽ n − 2),
a
′
n
−1, n−1
= a
ii
+
a
ji
+
a
jj
.
Для графов G и G
′
имеем соответственно матрицы смежности A, A
′
:
A
=
XXXXX
XXXXX
XXXX
0 2 1
1 1 0
0 1 0
XXXXX
XXXXX
XXXX
;
A
′
=
∥
0 1
1 4∥
.
Процедура «склеивания» вершин графа продолжается до тех пор, пока это
возможно. Если в матрице смежности полученного мультиграфа отличны от ну-
ля лишь элементы, стоящие на главной диагонали, то число компонент связности
исходного графа равно числу этих ненулевых элементов. Если же матрица смежно-
сти исходного графа становится вырожденной, то это означает, что граф содержит
лишь одну компоненту связности.
Матрица смежности графа G
′′
(рис. 2.27), который получен из графа G (рис. 2.25)
с помощью поэтапного применения операции склеивания вершин, является вырож-
денной, следовательно, граф G содержит только одну компоненту связности.

Контрольные вопросы по главе 2
45
. . . . . . . . . . . . . . . . . . . . . . . . .
Выводы
. . . . . . . . . . . . . . . . . . . . . . . . .
Изложенный способ позволяет построить алгоритм для подсчёта числа компо-
нент связности по матрице смежности «нового» графа, полученного на последней
итерации процедуры склеивания вершин.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Алгоритм для вычисления числа компонент связности графа.
Шаг 1. Найти ненулевой элемент матрицы смежности, не стоящий на главной
диагонали. Если он существует, перейти к шагу 2, если нет, то перейти к шагу 3.
Шаг 2. Произвести над матрицей операцию, отвечающую склейке вершин x
i
и x
j
, перейти к шагу 1.
Шаг 3. Подсчитать количество p строк матрицы, содержащих ненулевые эле-
менты на главной диагонали. Результат: число компонент связности графа равно p.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Контрольные вопросы по главе 2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Способы задания графов.
2. Классификация графов.
3. Что определяет метрика графа?
4. Чему равно расстояние между вершинами в графе?
5. Компоненты связности графа (определение).
6. Маршрут в графе (определение). Способы вычисления длины маршрута
в графе.
7. Определение связанного графа.
8. Понятие компоненты связанности графа.
9. Части графа.
10. Операции над графами. Унарные операции на графе: правило удаления
вершин и рёбер в графе, стягивание вершин по ребру, замыкания вершин.
11. Раскраска графа. Правильная раскраска вершин и рёбер графа. Хроматиче-
ское число графа.
12. Вершинные характеристики графа.
13. Внешне устойчивое множество графа.
14. Внутренне устойчивое множество графа.