Файл: Дискретная математика.pdf

26

Глава 2. Теория графов

Кольцевая сумма графов.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Кольцевая сумма графов представляет граф, который не имеет
изолированных вершин и состоит из ребер, присутствующих либо
в одном графе, либо во втором графе. Операция «кольцевая сумма
графов» обозначается символом

⊕:

G

= G

1

⊕ G

2

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

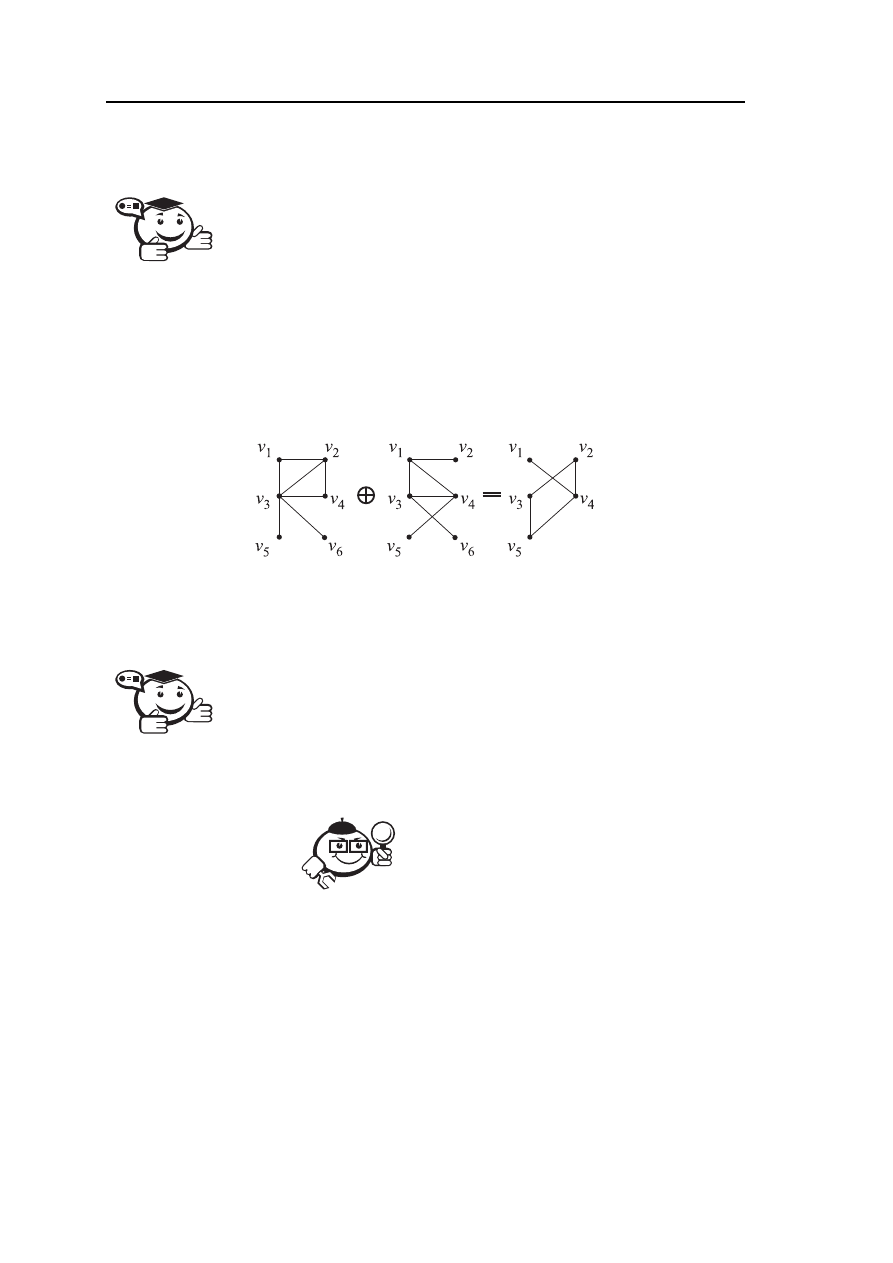
Пример выполнения операции «кольцевая сумма графов» G

1

и G

2

показан на

рисунке 2.9.

Рис. 2.9 – Пример операции «кольцевая сумма графов»

Пересечение графов.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Пересечение графов G

=

(V,X) и H = (U,Y) есть граф G ∩ H,

вершинами которого являются вершины, присутствующие одно-
временно и в графе G, и в графе H , а множество рёбер состо-
ит только из рёбер, присутствующих одновременно и в графе G,
и в графе H .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.6

. . . . . . . . . . . . . . . . . . . . .

Граф G называется пересечением графов G

1

, G

2

, если

V

G

= V

1

∩ V

2

и U

G

= U

1

∪ U

2

.

Операция «пересечения» записывается следующим образом: G

= G

1

∩ G

2

.

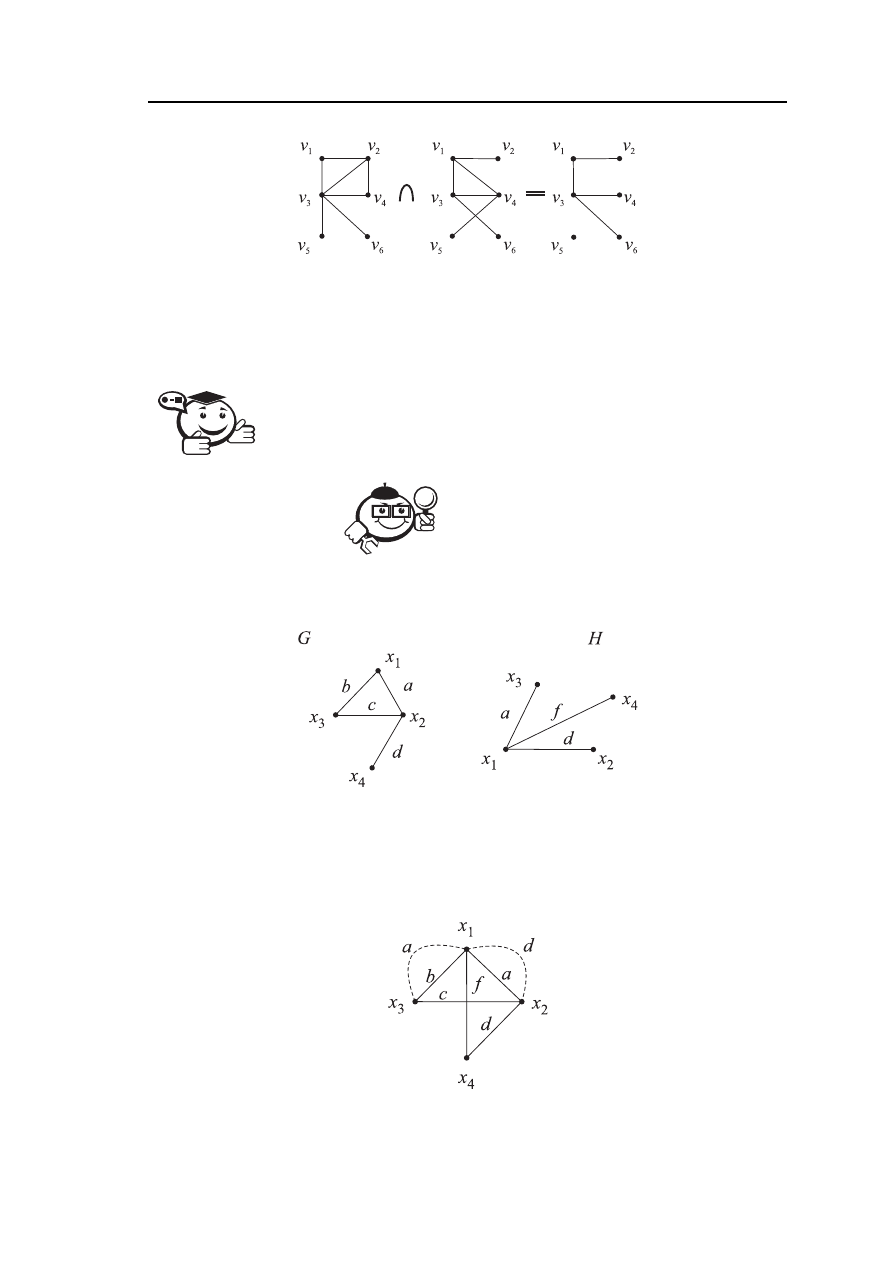
Пример операции «пересечения» графов представлен на рисунке 2.10.

2.6 Определение числа маршрутов длины «L» на графе

27

Рис. 2.10 – Операция «пересечение» графов

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Объединение графов.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Объединением графов G

=

(V,X) и H = (U,Y) называется граф

E

=

(V ∪ U, X ∪ Y).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.7

. . . . . . . . . . . . . . . . . . . . .

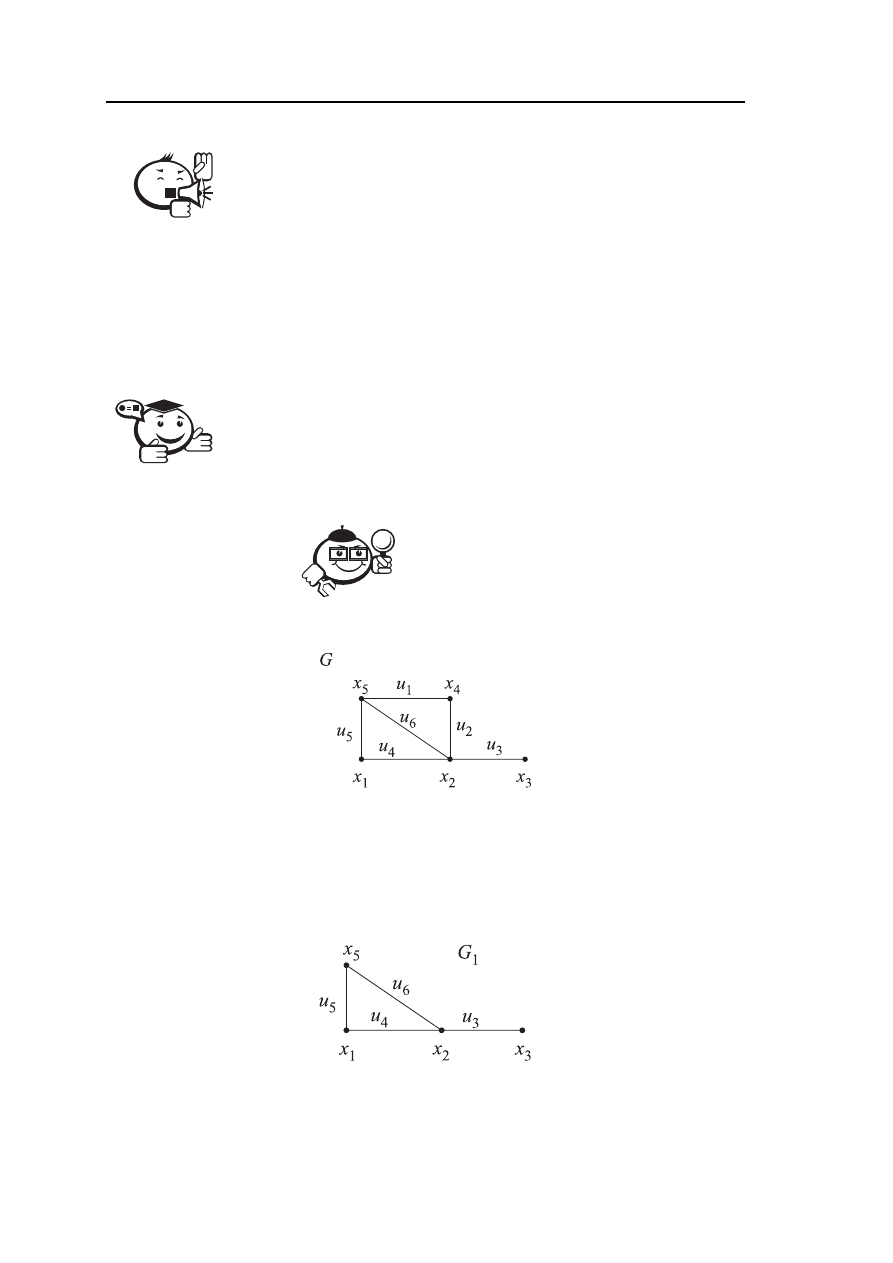
Выполнить операцию объединения графов G

(X,V) и H(Y,U), представленных

на рисунке 2.11.

Рис. 2.11 – Графы — G и H

Решение:
Граф E

=

(X ∪ Y, V ∪ U), полученный объединением графов G и H (рис. 2.12).

Рис. 2.12 – Граф E, полученный объединением графов G и H

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

28

Глава 2. Теория графов

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Операция объединения графов записывается: E

= G ∪ H.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.7 Части графа

2.7.1 Подграф

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Граф G

′

=

(X

′

, U

′

) называется подграфом графа G = (X,U), если

X

′

является подмножеством X

(X

′

⊂ X

), U

′

является подмноже-

ством U

(U

′

⊂ U

) и обе вершины каждого ребра из U

′

принадле-

жат X

′

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.8

. . . . . . . . . . . . . . . . . . . . .

В графе G (риc. 2.13) выделить два подграфа.

Рис. 2.13 – Граф G

Решение:
1. Граф G

1

(рис. 2.14) является подграфом графа G.

2. Граф G

2

(рис. 2.15) является подграфом графа G.

Рис. 2.14 – Граф G

1

— подграф графа G

2.7 Части графа

29

Рис. 2.15 – Граф G

2

— подграф графа G

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.7.2 Частичный граф

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Граф L

′′

=

(X

′′

, Y

′′

) является частичным графом (суграфом) графа

L

(X,U), если: X

′′

= X ; U

′′

является подмножеством U, т. е. U

′′

⊆ U.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.9

. . . . . . . . . . . . . . . . . . . . .

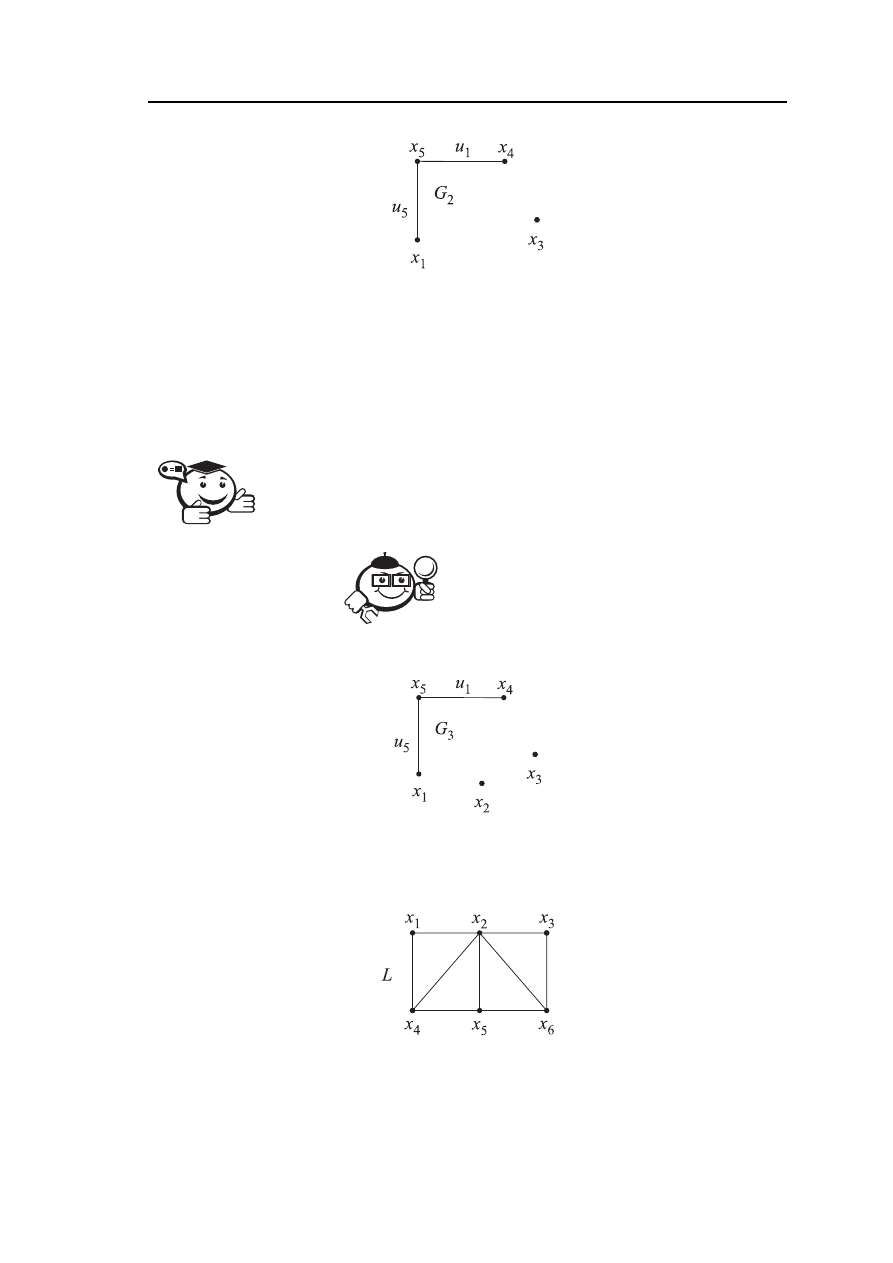
1. Граф G

3

(рис. 2.16) является частичным графом графа G (рис. 2.13).

Рис. 2.16 – Граф G

3

— частичный от графа G (рис. 2.13)

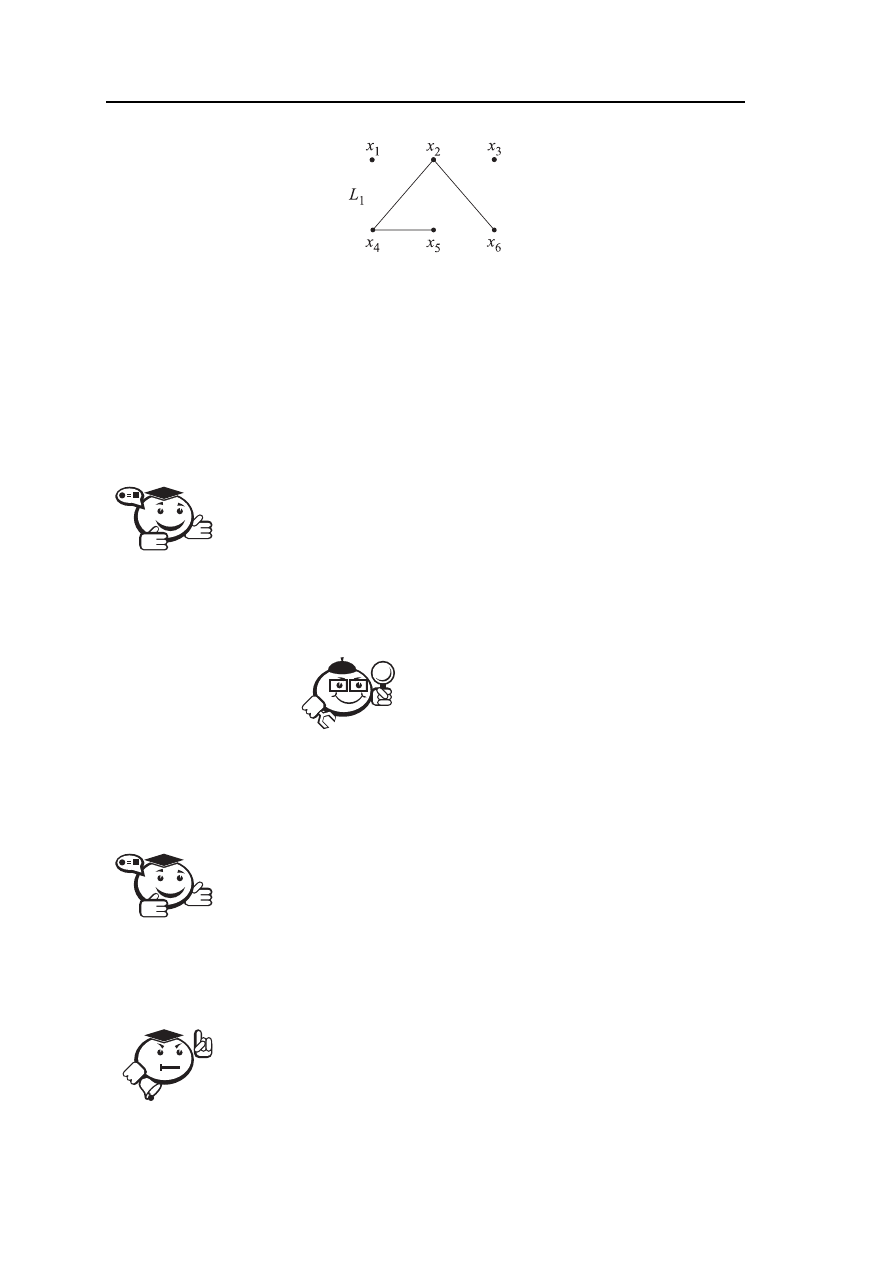
2. Граф L

1

(рис. 2.18) является частичным графом графа L (рис. 2.17).

Рис. 2.17 – Граф L

30

Глава 2. Теория графов

Рис. 2.18 – Граф L

1

— частичный граф от графа L

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.8 Метрика графа

Взвешенный граф

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Задавая на вершинах и рёбрах графа L

=

(X,U) функции p:

X

→ M

p

,

q: U

> M

q

,

где M

p

и M

q

— произвольные множества, получим взвешенный

граф L

(p,q) = (X,U,p,q).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.10

. . . . . . . . . . . . . . . . . . . . .

На множествах X и U можно задавать и более чем по одной функции или,

напротив, задать функцию только на рёбрах.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Вес ребра — значение, поставленное в соответствие данному ребру
взвешенного графа. Обычно, вес — вещественное число, которое
можно интерпретировать как «длину» ребра.

Взвешенный граф — граф, каждому ребру которого поставлено
в соответствие некоторое значение (вес ребра).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

К взвешенным графам принадлежат электрические схемы, сети
коммуникаций, информационные и логические сети, графы авто-
матов, сетевые графики работ и многое другое. Ограничимся здесь
отдельным вопросом, в котором наличие весов является идеей чи-
стой теории графов: длины рёбер.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .