ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7079
Скачиваний: 35
36
Глава 2. Теория графов
. . . . . . . . . . . . . . . . . . . . . .
Пример 2.12
. . . . . . . . . . . . . . . . . . . . .
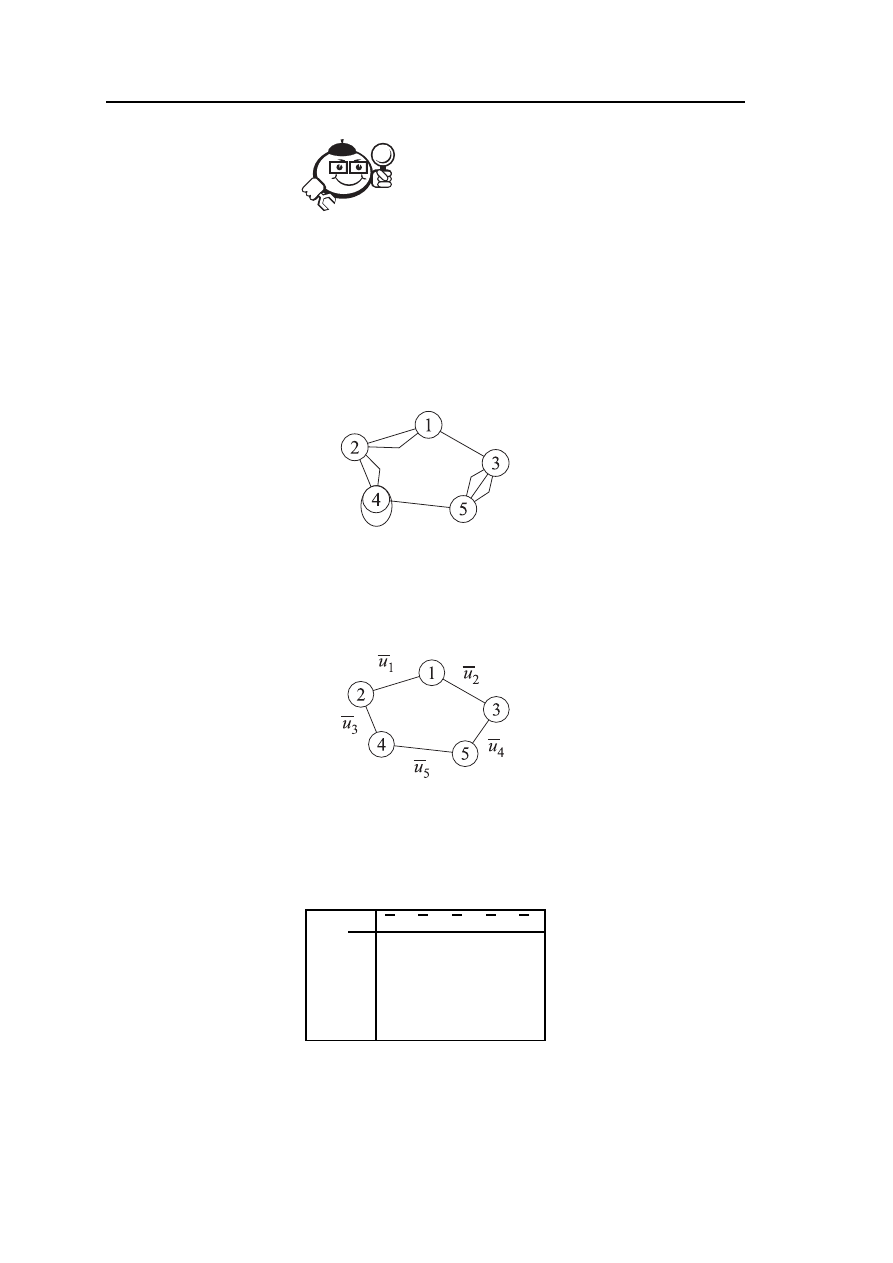
В графе L
=
(X,U;P), изображённом на рисунке 2.20, используя рассмотрен-
ный алгоритм, выделить все максимальные пустые подграфы.
Матрица смежности B графа L (рис. 2.20) содержит элементы b
ij
, равные:
b
11
= b
22
= b
33
= b
55
= 0; b
44
= 1; b
12
= 2; b
13
= 1; b
14
= 0; b
15
= 0;
b
21
= 2; b
23
= 0; b
24
= 2; b
25
= 0; b
31
= 1; b
32
= 0; b
34
= 0; b
35
= 3;
b
41
= 0; b
42
= 2; b
43
= 0; b
45
= 1; b
51
= 0; b
52
= 0; b
53
= 3; b
54
= 1.
Рис. 2.20 – Граф L
=
(X,U;P)
Решение:
Шаг 1. Для графа L строим скелет L
1
(рис. 2.21).
Рис. 2.21 – Скелет графа L
Шаг 2. Граф L
1
зададим его матрицей инциденций A (табл. 2.5).
Таблица 2.5 – Матрица инциденций A
A
=
u
1
u
2
u
3
u
4
u
5
1
1
1
0
0
0
2
1
0
1
0
0
3
0
1
0
1
0
4
0
0
1
0
1
5
0
0
0
1
1
Шаг 3. Введём логические переменные
{x
1
, x
2
, x
3
, x
4
, x
5
} в количестве, равном
числу вершин в графе L
1
, и матрицу A преобразуем в матрицу A
x
(табл. 2.6).
Шаг 4. Составим выражение для произведения
Π
L
:
Π
L
=
(x
1
+
x
2
)(x
1
+
x
3
)(x
2
+
x
4
)(x
3
+
x
5
)(x
4
+
x
5
).

2.9 Структурный анализ графов
37
Таблица 2.6 – Матрица A
x
A
x
=
u
1
u
2
u
3
u
4
u
5
1
x
1
x
1
0
0
0
2
x
2
0
x
2
0
0
3
0
x
3
0
x
3
0
4
0
0
x
4
0
x
4
5
0
0
0
x
5
x
5
Шаг 5. Преобразуем выражения
Π
L
к минимальной форме:
Π
L
=
(x
1
+
x
2
)(x
1
+
x
3
)(x
2
+
x
4
)(x
3
+
x
5
)(x
4
+
x
5
) =
(перемножаем скобки первую со второй и третью с пятой)
=
(x
1
+
x
2
x
3
)(x
4
+
x
2
x
5
)(x
3
+
x
5
) =
(перемножаем скобки первую со второй)
=
(x
1
x
4
+
x
1
x
2
x
5
+
x
2
x
3
x
4
+
x
2
x
3
x
5
)(x
3
+
x
5
) =
(перемножаем скобки)
= x
1
x
3
x
4
+
x
1
x
4
x
5
+
x
1
x
2
x
3
x
5
+
x
1
x
2
x
5
+
x
2
x
3
x
4
+
x
2
x
3
x
4
x
5
+
x
2
x
3
x
5
+
x
2
x
3
x
5
=
(минимизируем полученное выражение, применяя законы булевой алгебры)
= x
1
x
3
x
4
+
x
1
x
4
x
5
+
x
1
x
2
x
5
+
x
2
x
3
x
4
+
x
2
x
3
x
5
.
Преобразование выражения
Π
L
закончено. Получена минимальная форма по-
линома:
Σ
L
= x
1
x
3
x
4
+
x
1
x
4
x
5
+
x
1
x
2
x
5
+
x
2
x
3
x
4
+
x
2
x
3
x
5
.
Шаг 6. Выделим для каждого слагаемого полинома его дополнение до множе-
ства переменных
{x
1
, x
2
, x
3
, x
4
, x
5
}:
S
=
{(x
2
, x
5
); (x
2
, x
3
); (x
3
, x
4
); (x
1
, x
5
); (x
1
, x
4
)}.
Полученные дополнения порождают максимальные пустые подграфы графа L
1
и заданного графа L.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
Выводы
. . . . . . . . . . . . . . . . . . . . . . . . .
Алгоритм Магу—Вэйсмана может быть применён и для выявления в графе
L
=
(X,U; P) общего вида всех максимальных полных подграфов. Для этого необ-
ходимо построить для заданного графа L его скелет — граф L
1
, а для графа L
1
по-
строить дополнительный граф L (определение дополнительного графа дано в те-
ме 2.1 данного пособия). Получить дополнительный граф легко, если исходный
граф задать матрицей смежности его вершин, в которой всем элементам, равным
нулю, присвоить значение «1», а всем элементам, значения которых не равны ну-
лю, присвоить значение «0».
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
Глава 2. Теория графов
Далее для полученного графа L с помощью алгоритма Магу—Вэйсмана (рас-
смотренного выше) выявляем все максимальные пустые подграфы. Эти подграфы
являются максимальными полными подграфами для графов L
1
и L.
. . . . . . . . . . . . . . . . . . . . . .
Пример 2.13
. . . . . . . . . . . . . . . . . . . . .
В графе L= (V , U , P), приведённом на рисунке 2.20, выделить все максимальные
полные подграфы.
Решение:
Шаг 1. Строим скелет L
1
(рис. 2.21) графа L.
Шаг 2. Для графа L
1
строим его дополнительный граф L
′′
, представленный
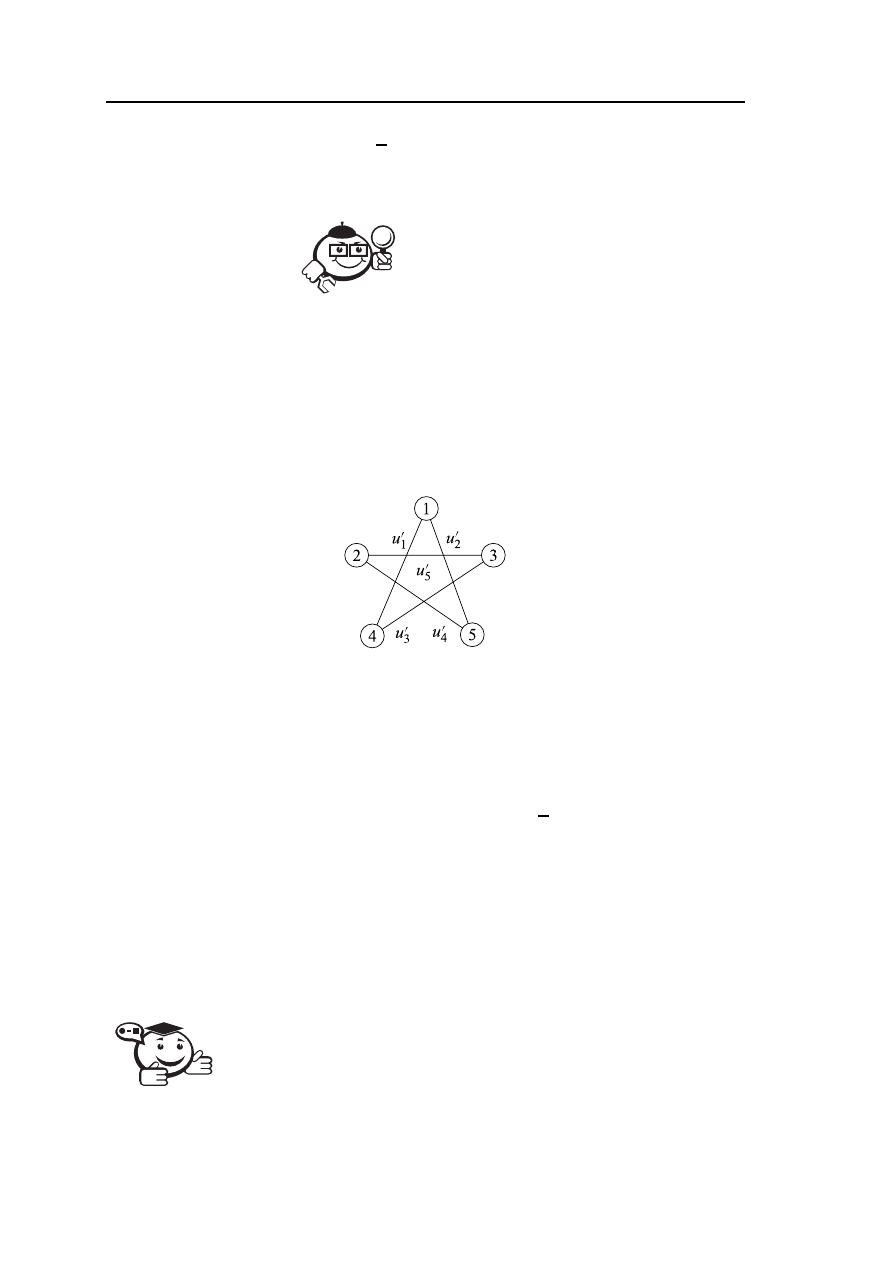
на рисунке 2.22, в котором с помощью алгоритма Магу—Вэйсмана выделим все
максимальные пустые подграфы.
Рис. 2.22 – Граф L
′′
=
(X,U
′
), где X = {1,2,3,4,5}, U
′
=
{u
′
1
, u
′
2
, u
′
3
, u
′
4
, u
′
5
}
Приведём окончательный результат решения данной задачи — полином графа L
′′
:
Σ
L
= x
1
x
2
x
3
+
x
1
x
2
x
4
+
x
1
x
3
x
5
+
x
2
x
4
x
5
+
x
3
x
4
x
5
и дополнения для его слагаемых:
(x
4
, x
5
); (x
3
, x
5
); (x
4
, x
2
); (x
1
, x
3
); (x
1
, x
2
), которые
порождают все максимальные пустые подграфы графа L и максимальные полные
подграфы заданного графа L
=
(V,U; P).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.9.1 Раскраска графов. Правильная раскраска,
хроматическое число
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Под раскраской графа понимают приписывание его вершинам
(рёбрам) какого-либо цвета.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Если в графе G
=
(X,U) его вершины (рёбра) раскрашены так, что смежные
вершины (рёбра) окрашены в разные цвета, то такую раскраску называют правильной.

2.9 Структурный анализ графов
39
Если на правильную раскраску затрачено p цветов, то граф называется p-хро-
матическим.
Наименьшее натуральное число p, для которого граф является p-хроматиче-
ским, называется хроматическим числом графа и обозначается
γ
(G).
Для решения задачи правильной раскраски графа G
=
(X,U) и определения
его хроматического числа можно применить алгоритм Магу—Вейсмана, который
подробно изложен в структурном анализе графов.
Раскраска графа с помощью метода Магу—Вейсмана выполняется в два этапа.
На первом этапе определяются подмножества вершин графа G, которые можно
раскрасить одним цветом.
На втором этапе определяется хроматическое число графа
γ
(G).
Для определения подмножества вершин, которые можно раскрасить одним
цветом, в графе G
=
(X,U) с помощью метода Магу—Вейсмана находятся все
максимальные пустые подграфы G
1
=
(X
1
, U
1
),G
2
=
(X
2
, U
2
),G
3
=
(X
3
, U
3
),...,G
i
=
=
(X
i
, U
i
),...,G
k
=
(X
k
, U
k
).
Очевидно, что вершины, принадлежащие одному подмножеству X
i
, можно рас-
крашивать одним цветом. Наибольшее число цветов P, необходимое для правиль-
ной раскраски вершин графа равно числу максимальных пустых подграфов дан-
ного графа.
Так как множества вершин X
1
, X
2
, X
3
, . . .X
i
, . . ., X
k
максимальных пустых под-
графов могут пересекаться, то число P, как правило, больше хроматического чис-
ла
γ
(G).
Алгоритм определения хроматического числа
γ
(G) с использованием метода
Магу—Вейсмана:
Шаг 1. Упорядочить все максимальные пустые подмножества X
1
, X
2
, X
3
, . . ., X
i
, . . ., X
k
графа G в порядке возрастания их кардинальных чисел —
∣X
i
∣.
Шаг 2. Выбрать подмножество X
i
, имеющее наибольшее значение кардиналь-
ного числа — max
∣X
i
∣.
Шаг 3. Присвоить цвет (допустим, синий) всем вершинам x
t
∈ max X
i
.
Шаг 4. Вычеркнуть из других подмножеств вершины, которым присвоен цвет.
Шаг 5. Исключить из дальнейшего рассмотрения подмножество X
i
.
Шаг 6. Если семейство пустых подмножеств X
1
, X
2
, X
3
, . . .X
i
, . . ., X
k
пусто, то
перейти к шагу 9, иначе — к шагу 7.
Шаг 7. Из оставшихся подмножеств X
1
, X
2
, X
3
, . . .X
i
, . . ., X
k
выбрать следующее
max
∣X
s
∣, где s ∈ I: I = {1,2,3,...,k}, и присвоить вершинам, входящим в него, цвет,
который ещё не использовался.
Шаг 8. Для max
∣X
s
∣ выполнить действия, описанные в шагах (4, 5, 6, 7), при-
нимая i
= s.
Шаг 9. Определить хроматическое число графа
γ
(G): подсчитать полученное
число подмножества вершин, «окрашенных » в разные цвета.
γ
(G) = количество цветов, потребовавшихся для раскраски в ходе выполнения
всех действий, описанных в шагах (1–8).
40
Глава 2. Теория графов
. . . . . . . . . . . . . . . . . . . . . .
Пример 2.14
. . . . . . . . . . . . . . . . . . . . .
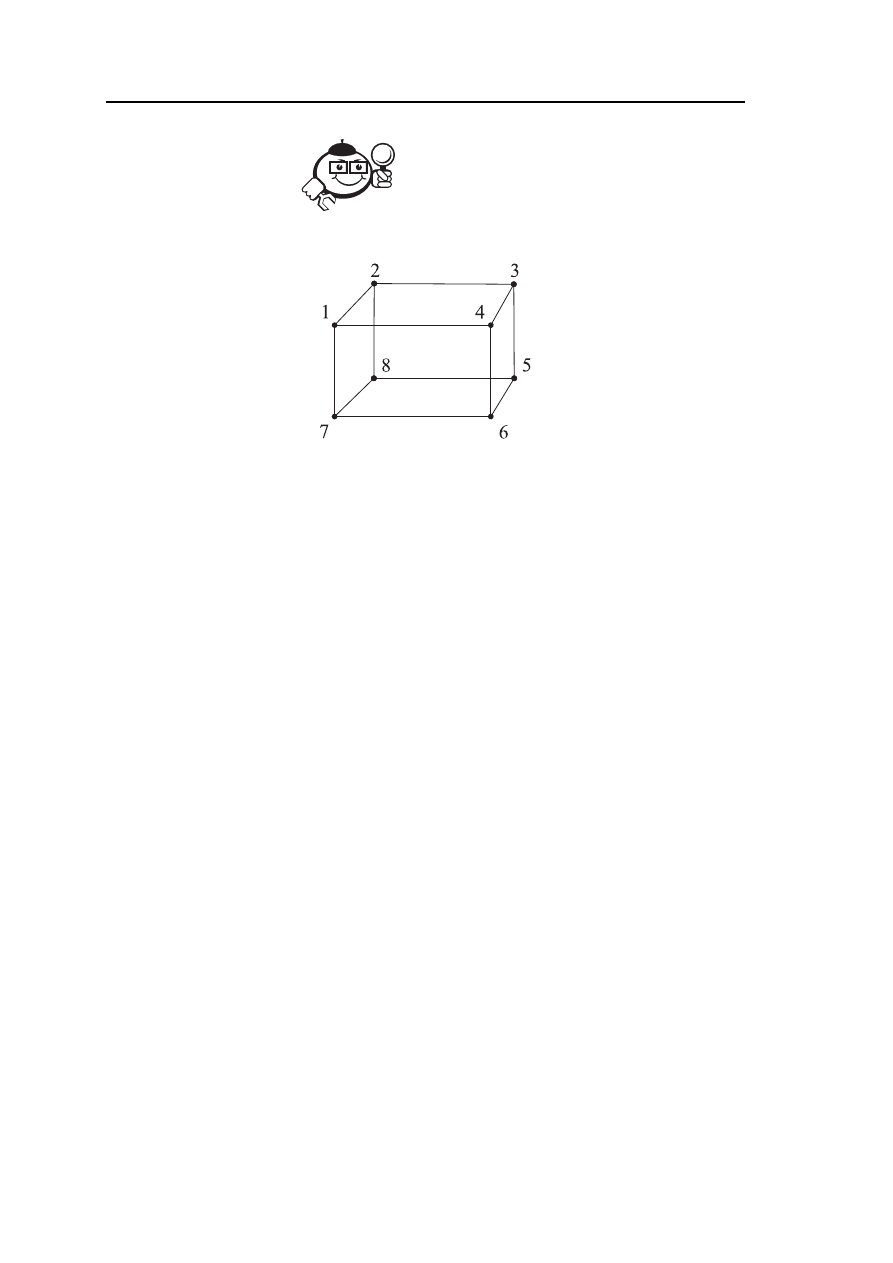
Найти раскраску вершин графа G
=
(X,U) (рис. 2.23).
Рис. 2.23 – Граф G
=
(X,U)
Решение:
1-й этап. Находим все максимальные пустые подграфы графа G
=
(X,U) с по-
мощью алгоритма Магу—Вейсмана.
1. Составляем произведение P
G
:
P
G
=
m
∏
j
=1
n
∑
i
=1
a
ij
⋅
x
i
,
где a
ij
— элемент матрицы инциденций графа G; a
ij
=
(0,1); x
i
∈ X — новые образу-
ющие, подчиняющиеся условиям:
(x
i
)
2
= x
i
,
(x
i
)
2
+
1
= 1, x
i
+
1
= 1, 1 + 1 = 1, 1 + 0 = 1
и законам коммутативности, ассоциативности и дистрибутивности, на основании
которых преобразуем выражение P
G
к минимальной бесскобочной форме.
P
G
=
(x
1
+
x
2
)(x
1
+
x
4
)(x
1
+
x
7
)(x
3
+
x
2
)(x
3
+
x
4
)(x
3
+
x
5
)×
×
(x
6
+
x
4
)(x
6
+
x
5
)(x
6
+
x
7
) × (x
8
+
x
2
)(x
8
+
x
5
)(x
8
+
x
7
) =
=
(x
1
+
x
2
x
4
x
7
)(x
3
+
x
2
x
4
x
5
)(x
6
+
x
4
x
5
x
7
)(x
8
+
x
2
x
5
x
7
) = ... =
= x
1
x
3
x
6
x
8
+
x
1
x
2
x
3
x
5
x
6
x
7
+
x
1
x
3
x
4
x
5
x
7
x
8
+
x
2
x
4
x
5
x
7
+
x
1
x
2
x
4
x
5
x
6
x
8
+
x
2
x
3
x
4
x
6
x
7
x
8
.
2. Для каждого слагаемого преобразованного выражения P
G
запишем его до-
полнение до полной системы образующих
{x
i
}, i = 1,2,...,8 —
x
2
x
4
x
5
x
7
; x
4
x
8
; x
2
x
6
; x
1
x
3
x
6
x
8
; x
3
x
7
; x
1
x
5
.
Получили полный обзор всех максимальных пустых подграфов графа G.
2-й этап. Переходим к раскрашиванию вершин графа G.
Будем кодировать цвета арабскими символами: 1, 2, 3, 4, 5, 6.
Всем вершинам, принадлежащим одному максимальному пустому подграфу
и ещё не раскрашенным, приписываем один цвет. Таким образом, для правильной
раскраски вершин графа G требуется шесть цветов, т. е. p
= 6.
Вывод. Граф G является 6-хроматическим.
3-й этап. Определяем хроматическое число
γ
(G) графа G.