Файл: Дискретная математика.pdf

Скачать файл (1,69Мб)

Заказать решение

ВУЗ: Томский государственный университет систем управления и радиоэлектроники

Категория: Учебное пособие

Дисциплина: Дискретная математика

Добавлен: 28.11.2018

Просмотров: 7077

Скачиваний: 35

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

2.8 Метрика графа

Пусть L

(q) = (X,U; q) — обыкновенный граф с весовой функцией q, относящей

каждому ребру u

∈ U действительное число q

(u) в качестве длины. Если M —

маршрут на графе L, то сумма q

(u) по всем рёбрам маршрута M называется его

q-длиной, а просто «длина» понимается как количество рёбер маршрута (каждое
ребро графа нужно считать столько раз, сколько оно встречается в маршруте).

Число

(x,y) = min{q(M)/M(M(x,y))},

(2.1)

где M

(x,y) — множество всех простых цепей из x в y называется расстоянием меж-

ду вершинами x, y

∈ X взвешенного графа L

(q); если x = y, то M — цепь нулевой

длины и её длина q

(M) = 0; если вершины x и y отделены в графе, то ρ(x,y) = +∞.

Термин «расстояние» оправдан тем, что функция

ρ, определённая посредством

выражения (2.1), удовлетворяет трём аксиомам метрики (аксиомы Фрише):

∀x, y ∈ X

[ρ(x,y) = 0 ⇒ x = y] (аксиома тождества),

(2.2)

∀x, y ∈ X

[ρ(x,y) = ρ(y,x)] (аксиома симметрии),

(2.3)

∀x, y ∈ X

[ρ(x,y) + ρ(y,z) = (x,z)] (аксиома треугольника),

(2.4)

т. е.

ρ является метрикой на множестве вершин X .

В частном случае, когда все q

(u) = 1 и, значит, q — длина всякой цепи совпа-

дает с её обычной длиной, метрика

= ρ

графа L

[1] называется естественной

метрикой обыкновенного графа L

= (X , U).

Вершина x

∈ X графа L = [q] называется центральной, если

∀x ∈ X [max ρ(x, y) ⩾ max ρ(x

, y

)],

∈ X , y ∈ X.

Вершина x

∈ X графа G = [q] называется периферийной, если

∀x ∈ X [max ρ(x, y) ⩽ max ρ(x

, y

)],

∈ X , y ∈ X.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Величина

(G) = min max ρ(x, y),

∈ X , y ∈ X

носит название радиуса графа.

Величина

(G) = max ρ(x, y),

x, y

∈ X

называется диаметром графа L

(X , U).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

У несвязного графа для любой пары вершин x, y

∈ X , max ρ(x, y) =

= +∞, поэтому каждая его вершина x является одновременно
и центральной, и периферийной, а радиус и диаметр бесконечны.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Глава 2. Теория графов

. . . . . . . . . . . . . . . . . . . . . .

Пример 2.11

. . . . . . . . . . . . . . . . . . . . .

Дан граф L

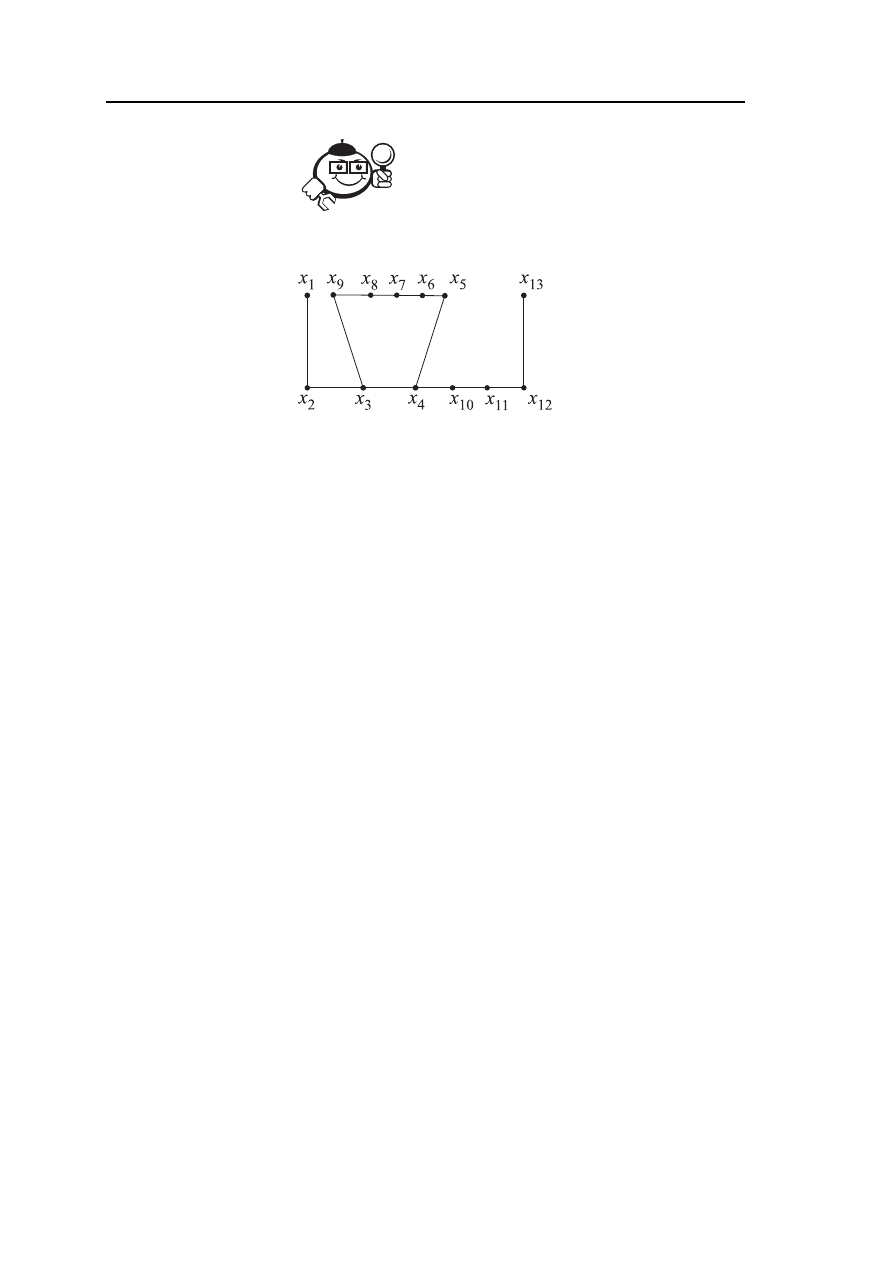
= (X , U) (рис. 2.19) с естественной метрикой ρ.

Рис. 2.19 – Граф L

(X , U), где X = {x

, x

, . . ., x

}

У данного графа вершины x

и x

— центральные, вершины x

, x

— пе-

риферийные, радиус r

(L) = 4, диаметр d(L) = 7.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Алгоритм вычисления значений элементов матрицы метрики
для графа общего вида

Для нахождения метрики

= ρ

графа L

= (X , U) достаточно знать его матри-

цу смежности R над булевой алгеброй B

= (0, 1), где элемент матрицы r

i j

= 1, если

вершины x

и x

— смежны, и r

i j

= 0, в противном случае.

Все дальнейшие действия над элементами матрицы R выполняются по прави-

лам алгебры логики Буля:

+ 1 = 1; 0 + 0 = 0; 1 + 0 = 1; 0 ⋅ 0 = 0; 1 ⋅ 0 = 0.

Сопоставляя уже известные нам способы для установления существования

в графе маршрутов длины l, можно утверждать, что при возведении в степень
матрицы S

= R + E, где E — единичная матрица той же размерности, что и размер-

ность матрицы R, на некотором шаге возведения в степень получим: S

= S

, т. е.

устойчивую матрицу S в степени «k».

Значения степеней k матрицы S

: k

= {1, 2, 3, . . ., t} равны длинам простых крат-

чайших цепей, связывающих вершины x

и x

Таким образом, последовательно возводя в степень k

= {1, 2, 3, . . ., t} матрицу S,

до получения устойчивой матрицы S

можно определить расстояния между всеми

вершинами графа L

= (X , U), построив матрицу метрики графа L.

Алгоритм построения матрицы метрики графа

Введём обозначения, которые будут использоваться в алгоритме построения

матрицы метрики (матрицы отклонений):

2.9 Структурный анализ графов

• L

= (X , U) — граф;

• R — матрица смежности заданного графа L;
• E — единичная матрица;
• M — матрица метрики;
• матрица смежности R графа L c элементами логического типа:

i,j

⎧⎪⎪

⎨⎪⎪

⎩

если вершины x

, x

— смежны;

в противном случае;

• S — матрица S

= R + E.

Значения элементов m

i,j

матрицы M определяются за несколько итераций по

результатам последовательного возведения матрицы S

(E + R) в степень k, где

{1,2,3,...,t} до получения устойчивой матрицы S

. Матрица S

называется

устойчивой, если S

= S

Шаг 1. Задаём матрицу метрики M

i,j

)

×n

. Размерность матрицы M равна

размерности матрицы R. Все элементы m

i,j

матрицы M не определены.

Шаг 2. Начальное значение степени k матрицы S равно «1»: k

= 1. ∀m

i i

при-

сваиваем значение «0», на основании 1-ой аксиомы Фрише.

Шаг 3. Всем элементам m

i,j

, значения которых не определены, присвоить зна-

чение степени k, если соответствующие им элементы матрицы S

≠ 0. (Значения

элементов m

i,j

определяются только один раз.)

Шаг 4. Повышаем степень k матрицы S: k

= k + 1.

Шаг 5. Проверяем, является ли матрица S

−1

устойчивой.

Если матрица S

−1

— неустойчивая, то переходим к шагу 3.

Иначе — переходим к шагу 6.
Шаг 6. Всем элементам m

i,j

матрицы M, значения которых остались неопреде-

ленными, присваиваем значение ∞ (бесконечность).

Шаг 7. Матрица метрики M

i,j

) построена. Конец алгоритма.

Примечание: Элементам

i,j

} значения присваиваются только один раз. Сле-

довательно, если значение элемента m

i,j

уже определено, то оно больше не меняется.

Радиус графа определяется по матрице метрики следующим способом: в каж-

дой строке матрицы M выделяется значение максимального элемента.

Наименьшее из выделенных значений — есть величина радиуса графа.
Диаметр графа также определяется по матрице метрики M следующим спосо-

бом: в каждой строке матрицы M выделяется значение максимального элемента.
Наибольшее из выделенных значений — есть величина диаметра графа.

2.9 Структурный анализ графов

Задача структурного анализа графов является одной из центральных задач тео-

рии графов и имеет широкое применение при решении фундаментальных теорети-
ческих проблем в программировании и прикладных задачах при анализе объектов
математических моделей.

Данная задача связана с базовыми понятиями: связность графа, компонента

связности графа, число компонент связности, полный граф, максимальные полные

Глава 2. Теория графов

подграфы (клика) и максимальные пустые подграфы, скелет графа. Рассмотрим
эти понятия.

Связность графа

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Говорят, что две вершины в графе G

(X,U) связаны, если суще-

ствует (простая) цепь, соединяющая их. Отношение связности вер-
шин является эквивалентностью. Классы эквивалентности по от-
ношению связности называются компонентами связности. Чис-
ло компонент связности графа G будем обозначать k

(G). Граф

G является связным тогда и только тогда, когда k

(G) = 1. Если

(G) > 1, то G — несвязный граф. Обозначим число вершин и чис-

ло рёбер графа G соответственно через

(G) и q(G). Граф, состо-

ящий только из изолированных вершин (в котором k

(G) = ρ(G)

и q

(G) = 0), называется вполне несвязным.

Скелет G

∧

графа G получается путём отбрасывания в графе G

всех петель и заменой кратных рёбер одним эквивалентным, а так-
же дезориентацией имеющихся дуг.

Говорят, что в графе G вершина покрывает инцидентные ей рёб-
ра, а ребро покрывает инцидентные ему вершины.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Множество вершин графа G, покрывающее все рёбра, называется вершинным

покрытием. Наименьшее число вершин во всех вершинных покрытиях называется
числом вершинного покрытия и обозначается

(G).

Множество таких рёбер, которые покрывают все вершины, называется рёбер-

ным покрытием. Наименьшее число рёбер во всех рёберных покрытиях называет-
ся числом рёберного покрытия и обозначается

(G).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Подграф L

′

называется максимальным пустым подграфом гра-

фа L

(X,U), если L

′

не является собственным подграфом ни-

какого большего максимального пустого подграфа данного графа L.

Подграф L

′′

называется максимальным полным подграфом графа

(X,U), если L

′′

не является подграфом никакого большего

максимального полного подграфа графа L.

Подмножество X

⊆ X вершин неорграфа G =

(X,U) называется

кликой, если G

) полный подграф (без петель) некоторого

неорграфа G

(X,Γ), соответствующего графу G = (X,U).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Клика X

k max

называется максимальной, если соответствующий ей подграф G

k max

строго не содержится ни в каком другом полном подграфе графа G.

2.9 Структурный анализ графов

Алгоритм нахождения всех максимальных пустых и всех
максимальных полных подграфов (максимальных клик)
в графе общего вида

Задача выявления всех максимальных полных и максимальных пустых подгра-

фов в заданном графе L

(X,U; P) общего вида легко сводится к случаю обыкно-

венных графов.

Поэтому для практического выявления всех максимальных полных и макси-

мальных пустых подграфов в произвольном неорграфе достаточно уметь выявлять
все максимальные полные и максимальные пустые подграфы в обыкновенных графах.

Рассмотрим алгоритм выявления всех максимальных пустых подграфов в неор-

графе общего вида, основанный на работах Х. Магу и Дж. Вэйсмана.

Шаг 1. Для графа L

(X,U; P) общего вида построить его скелет.

Шаг 2. Построить матрицу инциденций A графа L

(X,U) с элементами a

, где

= 1, n, j = 1, m, n =

∣X∣ — число вершин и m = ∣U∣ — число рёбер в графе L = (X,U).

Шаг 3. Ввести систему логических переменных x

, x

, . . ., x

, подчинив её

условиям, вытекающим из законов булевой алгебры:

2
i

= x

= 1,

а также законам коммутативности, ассоциативности и дистрибутивности.

Шаг 4. Матрицу инциденций A преобразовать в матрицу A

и составить про-

изведение

⎛

⎜⎜

⎜

⎝

. . . a

. . .

. . . a

⎞

⎟⎟

⎟

⎠

= Π

, x

, . . ., x

) =

∏

∑

где j-й сомножитель произведения

есть сумма двух слагаемых, соответствую-

щих тем двум вершинам, которые в графе L соединены j-м ребром.

Шаг 5. Преобразовать выражение произведения

к бесскобочному виду и при-

вести его к минимальной форме, применяя законы дистрибутивности, ассоциатив-
ности, коммутативности и закон поглощения:

а) a + a ⋅ b

= a; б)

(a + b)(a + c)...(a + p) = a + b ⋅ c...p,

где a, b, c, . . ., p — логические переменные, принимающие значения 0; 1, выполняя
при этом условия, описанные в шаге 3. В результате выполненных преобразова-
ний выражение

будет иметь минимальную форму и представлять выражение

суммы произведений переменных из множества x

, x

, . . ., x

, т. е. многочлен.

Обозначим его

Шаг 6. Для каждого слагаемого многочлена

выделить переменные, кото-

рые в него не входят, но входят в множество

, x

, . . ., x

}. Эти переменные