4. Как влияет давление газа на его электрическую прочность?

5. Как внешне проявляется процесс пробоя в газообразных диэлектриках?

ПРОВОДНИКИ

К проводникам электрического тока относятся как твердые тела, так и жидкости, а при соответствующих условиях и газы. Важнейшими практически при­меняемыми в электротехнике твердыми проводниковыми материа­лами являются металлы и их сплавы.

Из металлических проводниковых материалов могут быть выде­лены металлы высокой проводимости, имеющие удельное сопротив­ление  при нормальной температуре не более 0,05 мкОм м, и сплавы высокого сопротивления, имеющие  при нормальной температуре не менее 0,3 мкОм м. Металлы высокой проводимости используются для проводов, токопроводящих жил кабелей, обмоток электриче­ских машин и трансформаторов и т. п. Металлы и сплавы высокого сопротивления применяются для изготовления резисторов, электро­нагревательных приборов, нитей ламп накаливания и т. п.

К жидким проводникам относятся расплавленные металлы и различные электролиты. Для большинства металлов температура плавления высока, только ртуть, имею­щая температуру плавления около минус 39 °С, может быть исполь­зована в качестве жидкого металлического проводника при нормаль­ной температуре. Другие металлы являются жидкими проводниками при повышенных температурах.

Механизм прохождения тока в металлах – как в твердом, так и в жидком состоянии – обусловлен движением (дрейфом) свободных электронов под воздействием электрического поля; поэтому металлы называют проводниками с электронной электропроводностью или проводниками первого рода. Проводниками второго рода, или электро­литами, являются растворы (в частности, водные) кислот, щелочей и солей. Прохождение тока через эти вещества связано с переносом вместе с электрическими зарядами ионов в соответствии с законами Фарадея, вследствие чего состав электролита постепенно изменя­ется, а на электродах выделяются продукты электролиза. Ионные кристаллы в расплавленном состоянии также являются провод­никами второго рода. Примером могут служить соляные закалоч­ные ванны с электронагревом.

Общие представления о зонной теории электропроводности твердых тел были даны в ведении.

Классическая электронная теория металлов представляет твер­дый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных (свободных) электронов. В свободное состоя­ние от каждого атома металла переходит от одного до двух электро­нов. К электронному газу применялись представления и законы статистики обычных газов. При изучении хаотического (теплового) и направленного под действием силы электрического поля движения электронов был выведен закон Ома. При столкновениях электронов с узлами кристаллической решетки энергия, накопленная при уско­рении электронов в электрическом поле, передается металлической основе проводника, вследствие чего он нагревается. Рассмотрение этого вопроса привело к выводу закона Джоуля–Ленца. Таким образом, электронная теория металлов дала возможность аналитически описать и объяснить найденные ранее экспериментальным путем основные законы электропроводности и потерь электрической энергии в металлах.

---

Выявленные противоречия некоторых выводов теории с опытными данными удалось преодолеть, рассматривая некоторые положе­ния с позиций квантовой механики. В квантовой механике принимается, что электронный газ в металлах при обычных температурах находится в состоянии вырождения. В этом состоянии энергия электронного газа почти не зависит от температуры, т. е. тепловое движение почти не изменяет энергию электронов. Представляя металл как систему, в которой положительные ионы скрепляются посредством свободно движущихся электронов, легко понять природу всех ос­новных свойств металлов: пластичности, ковкости, хорошей тепло­проводности и высокой электропроводности.

К важнейшим параметрам, характери­зующим свойства проводниковых материалов, относятся: 1) удельная проводимость  или обратная ей величина – удельное сопротивление , 2) температурный коэффициент удельного сопротивления ТК_ или _, 3) коэффициент теплопроводности _т, 4) контактная раз­ность потенциалов и термоэлектродвижущая сила (термо-ЭДС), 5) работа выхода электронов из металла, 6) предел прочности при растяжении _р и относительное удлинение перед разрывом l/l.

Лабораторная работа № 6

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО
СОПРОТИВЛЕНИЯ ПРОВОДНИКА

6.1. Цель работы

6.2. Задачи работы

Определить удельные сопротивления исследуемых образцов и сравнить со справочными данными.

6.3. Краткие теоретические сведения

С позиции классической электронной теории металлы рассмат­риваются как система, состоящая из положительных ионов, обра­зующих узлы кристаллической решетки, и свободных (коллективи­зированных) электронов – электронов проводимости, заполняющих остальное пространство решетки.

Электрический ток в металлических проводниках обусловлен упорядоченным движением – дрейфом электронов проводи­мости под действием внешнего электрического поля.

Количественно это явление описывается законом Ома. Согласно закону Ома в дифференциальной форме плотность тока пропорцио­нальна напряженности поля:

j =  Е,

где j — плотность электрического тока, А/м²; Е — напряженность поля, В/м;  – коэффициент пропорциональности, представляющий удельную электропроводность, См/м.

На основании классической электронной теории удельная элек­тропроводность у металлов определяется выражением:

, (6.1)

где е — заряд электрона, Кл = А с; п – концентрация электронов про­водимости, м^–3; а — подвижность электронов, обусловленная действи­ем электрического поля, м²/(В с), (а = v_cp.дp/E= eE/E2m = e/2mv);  – средняя длина свободного пробега электрона между двумя столк­новениями с решеткой в ускоряющем поле напряженностью Е, м; т – масса электрона, кг; v – средняя скорость теплового движения электронов в металле, м/с;  – время между двумя столкновениями, с; v_cp.дp – среднее значение дрейфовой скорости, м/с.

---

У всех металлов величину средней скорости v теплового дви­жения можно считать постоянной. Концентрация п электронов проводимости, как и скорость v, мало зависит от природы метал­ла. Поэтому удельная электропроводность  металлических про­водников зависит в основном от средней длины свободного про­бега электрона , величина которой существенно влияет на подвижность а электронов: чем меньше , тем меньше а. Величи­на , в свою очередь зависит от степени деформации кристаллической решетки металлического проводника. У идеального металли­ческого проводника при температуре, равной 0 К, электроны проводимости не будут сталкиваться с узлами кристаллической решетки, поэтому длина свободного пробега электрона  и, следо­вательно, электропроводность  должны быть бесконечно больши­ми, а удельное сопротивление  равно нулю.

Зависимость удельной проводимости ρ от концентрации и свободных зарядов легко получить, используя закон Ома для участка цепи:

(6.2)

где I – сила тока протекающего по участку цепи; R – сопротивление участка цепи; U – напряжение на концах участка цепи.

Сопротивление проводника простейшим способом определяют, используя закон Ома для участка электрической цепи. Для этого нужно измерить вольтметром разность потенциалов U на концах проводника и амперметром силу тока I в проводнике и поделить одно на другое. Этот метод измерений (по току и напряжению) называют техническим. Однако при таком способе измерения вносятся систематические ошибки, величина которых зависит от сопротивлений измерительных приборов и величины измеряемых сопротивлений.

Действительно, при включении приборов по схеме на рис. 6.1 показания вольтметра соответствуют напряжению на сопротивлении (U_V = U), но показания амперметра соответствуют не току через сопротивление, а сумме токов через проводник и вольтметр:

I_A = I_V + I (6.3)

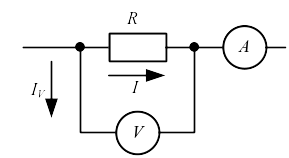
Рис. 6.1. Схема электрическая принципиальная измерения сопротивления вольтметром и амперметром

При включении по схеме на рис. 6.2 показания амперметра соответствуют току через сопротивление (I_A = I), но вольтметр показывает не напряжение на сопротивлении, а суммарное напряжение на сопротивлении и амперметре:

U_V= IR + IR_A (6.4)

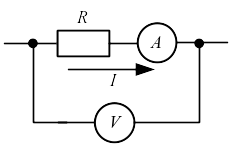
Рис. 6.2. Схема электрическая принципиальная измерения сопротивления вольтметром и амперметром

Из выражений (6.3) и (6.4) следует, что для уменьшения погрешностей, вносимых при подключении приборов, сопротивление амперметра должно быть малым, а сопротивление вольтметра – большим. Данный метод лежит в основе работы омметров. Прибор прикладывает известную разность потенциалов к измеряемому сопротивлению и измеряет протекающий ток.

Мостовые схемы измерения сопротивлений позволяют избавиться от ошибок, вносимых электроизмерительными приборами, так как здесь эти приборы используются не для измерения силы тока и напряжения, идущих в дальнейшие расчеты, а только в качестве чувствительных индикаторов, работающих либо в режиме постоянного показания, либо, чаще, в режиме отсутствия тока (нуль-метод).

---

Схема моста Уитстона составлена из сопротивлений R_x, R₁, R₂, R₃, образующих плечи моста (рис. 6.3). В одну из диагоналей мостовой схемы CD включается чувствительный измеритель тока – миллиамперметр. К другой диагонали АВ подключается источник питания с сопротивлением R_д. В плечи моста АС и DВ включаются известные сопротивления R₂ и R₃. В плечо AD включается измеряемое сопротивление R_x, а в плечо СВ – магазин сопротивлений. Магазин сопротивлений представляет собой набор достаточно точных переменных сопротивлений. Процесс измерения по этой схеме заключается в подборе такого сопротивления магазина, при котором миллиамперметр в диагонали СD показывает отсутствие тока.

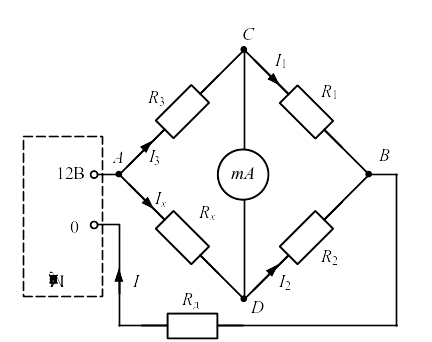
Рис. 6.3. Схема моста Уитстона

При произвольном соотношении сопротивлений через все плечи моста и через гальванометр идут токи. Изменяя сопротивление магазина, добиваются такого состояния, при котором потенциалы точек С и D будут одинаковыми, и ток через миллиамперметр станет равным нулю. Это состояние схемы называется равновесием моста.

В состоянии равновесия разность потенциалов между точками А и С равна разности потенциалов между точками А и D, а
φ_C – φ_B = φ_D – φ_B. В соответствии с законом Ома для пассивного участка электрической цепи разность потенциалов на концах участка равна падению напряжения на участке – произведению силы тока на сопротивление этого участка цепи: φ₁ – φ₂ = IR. Приравнивая падения напряжения на сопротивлениях R_x и R₃, R₁ и R₂, получим следующие выражения:

I₃R₃ = I_xR_x (6.5)

I₁R₁ = I₂R₂ (6.6)

Эти равенства справедливы только тогда, когда мост находится в состоянии равновесия. Так как ток в диагонали СD при этом равен нулю, то ток I₁ протекающий по сопротивлению R₁, равен току I₃, протекающему по сопротивлению R₃, а ток I_x, протекающий по сопротивлению R_x, равен току I₂, протекающему по магазину сопротивлений R₂. Разделив уравнение (6.5) на уравнение (6.6), получим условие равновесия моста Уитстона:

. (6.7)

Из него следует, что если установить ток в гальванометре равным нулю, то неизвестное сопротивление _Rx определяется по остальным трем сопротивлениям:

(6.8)

Активное сопротивление зависит от формы и размеров проводника:

(6.9)

Для однородного проводника с поперечным сечением S и длиной l:

(6.10)

6.4. Используемое оборудование

Модуль «Измеритель RLC», «Модуль питания», образцы ис­следуемых проводников, соединительные проводники.

6.5. Задание на выполнение лабораторной работы

1. Измерить сопротивления проводников R и вычислить удельное сопротивление материалов .

2. Сравнить полученные результаты со справочными.

6.6. Программа работы

1. Прочитать методические указания по подготовке и проведению лабораторной работы.

2. Получить у преподавателя вариант задания исходных данных к работе.

3. При ознакомлении с рабочим местом проверить наличие необходимых приборов и соединительных проводников (в случае отсутствия какого-либо ком­плектующего элемента типового комплекта необходимо немедленно сообщить об этом преподавателю или техническому персоналу);

---

4. Перед сборкой цепи проверить, чтобы все приборы на рабочем столе бы­ли выключены;

5. Подать питание на комплект включением автоматического выключателя и УЗО «Модуля питания и измерений». Установить соединительные проводники в гнёзда RLС-метра, как указано на рисунке 1.9, выбрать режим измерения со­противлении, нажимая кнопку L/C/R; диапазон измерения выбирается автомати­чески при измерении. Измерить сопротивление проволоки. Измерить сопротив­ление проволоки на участке различной длины (от 0,1 м до 0,5 м) с шагом 0,05–0,15 м (рис. 6.4). Так как проволока не имеет собственной изоляции, необходимо расположить её таким образом, чтобы она не соприкасалась сама с собой и дру­гими металлическими предметами. Измеренное сопротивление и длину участка заносить в табл. 6.1.

Таблица 6.1

l1, м
R1, Ом
l2, м
R2, Ом
….
ln, м
Rn, Ом

В табл. l_i – длина измеренного участка i-ой проволоки, R_i – сопротивление участка длинной l_i i-ой проволоки/

6. Повторить измерения в соответствии с пунктом 2 с другой проволокой.

7. Построить график зависимости R(l). При построении графика учесть, что прямая не будет проходить через точку (0,0) так как RLC-метр и его щупы имеют собственное сопротивление. По графику определить коэффициент , как тангенс угла наклона графика. Значение коэффициента заносить в табл. 6.2.

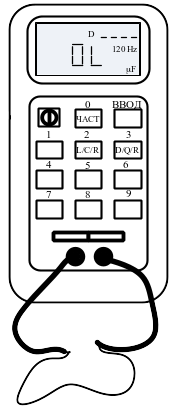
Рис. 6.4. Измерение сопротивления проволоки RLC-метром

6. Повторить измерения в соответствии с пунктом 2 с другой проволокой.

7. Построить график зависимости R(l). При построении графика учесть, что прямая не будет проходить через точку (0,0) так как RLC-метр и его щупы имеют собственное сопротивление. По графику определить коэффициент , как тангенс угла наклона графика. Значение коэффициента заносить в табл. 6.2.

Таблица 6.2

Исследуемая проволока		d	S	ρ
1
2
…
n

Из формулы (6.10) видно, что

,

таким образом, найдем удельное сопротивление

.

Площадь сечения S рассчитать, как площадь круга:

,

где d – диаметр исследуемой проволоки (указан на ярлыке).

Заполнить табл. 6.2, значения рассчитывать по вышеприведенным фор­мулам.

8. Сравнить полученные значение ρ с табличными значениями, указать ис­точник справочной информации. По полученным результатам сделайте вывод о материале, из которого изготовлена каждая исследованная проволока.

---

Смотрите также файлы

• Макро 2 семестр.docx

• Компьютерный английский Met_196.doc

• Информатика.docx

• Задачи по физике.docx

• дневник ПГС.doc