Добавлен: 31.01.2019
Просмотров: 4560
Скачиваний: 45
Третья составляющая термоэдс возникает в контуре вследствие увлечения электронов квантами тепловой энергии (фононами). Их поток также распространяется к холодному концу. Все составляющие термоэдс определяются небольшой концентрацией электронов, расположенных на энергетических уровнях, близких к уровню Ферми, и отстоящих от него на величину порядка kT. Поэтому удельная термоэдс для металлов оказывается очень небольшой. Квантовая теория дает следующее выражение для удельной термоэдс одновалентных металлов:
![]() (8.3)
(8.3)
где k =1,38 10–23Дж/К – постоянная Больцмана, e = –1,6 10–19 – заряд электрона.
При комнатной температуре отношение kT/WF имеет значение порядка 10-3 . Поэтому Т должна составлять несколько мкВ/К.
Существенно большее значение удельной термоэдс можно получить при использовании металлических сплавов, которые имеют сложную зонную структуру.
Металлические термопары широко используются для точного измерения температуры. В процессе измерений необходимо стабилизировать температуру одного из спаев.
В реальных условиях полностью исключить перепады температуры практически невозможно. Поэтому в электрических цепях могут возникать паразитные термоэдс. Для уменьшения их влияния в цепях электроизмерительных приборов следует подбирать контактирующие материалы с малыми значениями Т.
8.4. Используемое оборудование
«Модуль питания», модуль «Магнитомягкие материалы и тепловой коэффициент сопротивления / емкости», модуль «Мультиметры», «ТКС проводников», соединительные проводники.
8.5. Задание на выполнение лабораторной работы
1. Измерить термоэдс U и разность температур горячего спая tг и свободных концов tс.
2. На основании формулы (8.2) вычислить удельную термоэдс исследуемой термопары.
8.6. Программа работы
1. Прочитать методические указания по подготовке и проведению лабораторной работы.
2. Получить у преподавателя вариант задания исходных данных к работе.
3. При ознакомлении с рабочим местом проверить наличие необходимых приборов и соединительных проводников (в случае отсутствия какого-либо комплектующего элемента типового комплекта необходимо немедленно сообщить об этом преподавателю или техническому персоналу);
4. Перед сборкой цепи проверить, чтобы все приборы на рабочем столе были выключены;
5. Согласно рисунку 1.12 выполнить электрические соединения модулей. Монтаж схемы производить при отключенном питании.
В качестве нагревателя использовать минимодуль «ТКС проводников» (он оснащен двумя термопарами).
В качестве источника питания для нагрева «15В» использовать нерегулируемый выход модуля питания «15В».
В качестве термометра Р1 использовать мультиметр в режиме измерения температуры «С0».
В качестве вольтметра PV1 использовать мультиметр в режиме измерения постоянного напряжения с пределом 200 мВ. Для подключения исследуемой термопары к вольтметру необходимо использовать щупы с зажимами. Подключить «+» термопары к гнезду «VΩHz» мульгиметра P1, а «–» к гнезду «СОМ».

Рис. 8.3. Схема электрическая соединений типового комплекта для измерения термоэдс
После проверки правильности соединений схемы преподавателем или лаборантом, подать напряжение питания на комплект включением автоматического выключателя и УЗО «Модуля питания».
Включить мультиметры. Если термопара не соединена с гнездами мультиметра Р1, на его индикаторе будет отображаться комнатная температура (комнатная температура равна температуре свободных концов tс). Соединить термопару с гнездом «ТЕМР» мультиметра Р1 и, в случае если показания температуры на мультиметре ниже комнатной, изменить полярность подключения выводов термопары (перевернуть вилку). Заносить значение температуры в табл. 8.1.
Таблица 8.1
-
Температура свободных концов tс, С0
№п.п.
tг, 0C
U, В
tг – tс, 0C
т
1
2
….
6. Измерить температуру рабочего спая tг мультиметром P1 и термоэдс U мультимегром PV1. Значения заносить в табл. 8.1.
7. Заносить показания мультиметров в табл. 8.1 через 5 – 10С°. Не нагревать минимодуль более 100С°.
8. Рассчитать разность температур рабочего спая и свободных концов термопары, для каждого пункта табл. 8.1.
9. Построить график зависимости U(tг – tс). По графику определить относительную удельную термоэдс т, как тангенс угла наклона графика, и сравнить со справочным значением для данной термопары.
10. После оформления отчета и проверки результатов преподавателем необходимо разобрать схему, предоставить комплект в полном составе и исправности преподавателю или лаборанту.
8.7. Содержание отчета
1. Название работы. Цель работы.
2. Используемое оборудование и схемы электрических соединений.
3. Результаты измерений.
4. Результаты расчётов и построенные опытные зависимости (графики).
5. Краткие выводы по каждой работе, анализ полученных результатов:
– сравнение опытных зависимостей (графиков) с теоретическими;
– сравнение полученных экспериментальных значений с табличными, с обязательными ссылками на источники информации;
– сопоставление их расхождений с точностью измерений.
6. Обобщающий вывод по всей лабораторной работе. Вывод включает в себя:
а) основные численные результаты работы;
б) погрешность измерений, в случае относительной погрешности более 15% обязательны анализ и указание причин, приведших к снижению точности эксперимента.
8.8. Контрольные вопросы
1. В каких условиях возможно появление термоэдс в замкнутой цепи?
2. Назовите основные механизмы возникновения термоэдс.
3. Приведите определение рабочего спая термопары?
4. Каков физический смысл относительной удельной термоэдс?
ПОЛУПРОВОДНИКИ
Большая группа материалов с электронной п и дырочной р проводимостью, удельное сопротивление которых при температуре 20 °С больше, чем у проводников, но меньше, чем у диэлектриков, относится к полупроводникам. С точки зрения зонной теории твердого тела, к полупроводникам относятся те материалы, ширина запрещенной зоны (33) которых имеет величину в пределах от 0,05 до 3 эВ.
Электрофизические характеристики полупроводниковых материалов зависят не только от их природы, но и от интенсивности внешнего энергетического воздействия, природы и концентрации легирующей примеси – примеси, которую специально вводят в полупроводниковый материал для создания определенного типа и величины электропроводности. Полупроводниковый материал, используемый для изготовления приборов, должен иметь очень высокую степень чистоты.
Управляемость удельной электропроводностью полупроводниковых материалов посредством температуры, света, электрического поля, механического напряжения положена в основу принципа действия соответствующих приборов: терморезисторов, фоторезисторов, нелинейных резисторов (вариаторов), тензорезисторов и т.д.
Наличие двух или более взаимно связанных p-n-переходов образуют управляемые системы – кристаллические транзисторы и тиристоры. Полупроводниковые системы широко используют для преобразования различных видов энергии в электрическую и наоборот.
Величина и тип электропроводности полупроводников зависят от природы и концентрации примеси, в том числе специально введенной (легирующей).
Концентрация легирующей примеси обычно незначительна, например у Ge она составляет один атом на 1010–1012 атомов полупроводника. В этой связи все полупроводники можно разбить на две группы: собственные и примесные.
Собственные полупроводники не содержат легирующие примеси; к ним относятся высокой степени чистоты простые полупроводники: кремний Si, германий Ge, селен Se, теллур Те и др. и многие полупроводниковые химические соединения: арсенид галлия GaAs, антимонид индия InSb, арсенид индия InAs и др.
Примесные полупроводники всегда содержат донорную или акцепторную примесь. В производстве полупроводниковых приборов примесные полупроводники используют чаще, поскольку в них свободные носители заряда образуются при более низких температурах (чем в собственных полупроводниках), которые отвечают рабочему интервалу температур полупроводникового прибора.
Электропроводность собственных полупроводников. В собственных полупроводниках при достаточности тепловой энергии решетки или в результате внешнего энергетического воздействия электрон(ы) перейдет(ут) из валентной зоны (ВЗ) в зону проводимости (ЗП) и станет(ут) свободным(и). Необходимая для этого перехода энергия определяется шириной запрещенной зоны (33) – W полупроводника. При комнатной температуре эта энергия может возникать вследствие флуктуации тепловых колебаний решетки (средней тепловой энергии решетки для такого перехода недостаточно). С уходом электрона в ЗП в валентной зоне остается свободным энергетический уровень, называемый дыркой, а сама ВЗ становится не полностью заполненной (рис. __, а). Электрон имеет отрицательный заряд, дырку принято считать положительно заряженной частицей, численно равной заряду электрона.

Рис. ____. Энергетические диаграммы полупроводников:
а – полупроводник без лигирующей примеси; б – полупроводник (p-типа) с акцепторной примесью; в – полупроводник (n-типа) с донорной примесью; Wa – энергия активации (образования) дырок в ВЗ полупроводника за счет перехода электронов на уровни акцепторной примеси; Wд – энергия активации электронов – энергия, необходимая для перехода электронов с уровней донорной примеси в ЗП полупроводника
Таким образом, в кристалле образуется пара свободных носителей заряда — электрон в ЗП и дырка в ВЗ, которые и создают собственную электропроводность полупроводника, тип которой электронно-дырочный.
В отсутствие внешнего электрического поля электрон и дырка совершают тепловые хаотические движения в пределах кристалла, а под действием поля осуществляют дополнительно направленное движение – дрейф, обусловливая тем самым электрический ток. Если концентрации свободных электронов и дырок равны между собой, то подвижность у них различна. В результате более низких значений эффективной массы и инерционности при движении в поле кристаллической решетки свободные электроны более подвижны, чем дырки. Поэтому собственная электропроводность полупроводников имеет слабо преобладающий электронный тип.
Электропроводность примесных полупроводников. В примесных полупроводниках атомы примеси либо поставляют электроны в ЗП полупроводника, либо принимают их с уровней ВЗ. Эти переходы электронов осуществляются при существенно меньших затратах энергии, которые требуются электронам для преодоления потенциального барьера в виде 33 полупроводника. Поэтому эти виды переходов в примесных полупроводниках являются основными, доминирующими над переходом электронов из ВЗ в ЗП.
Атомы примеси, размещаясь в запрещенной зоне полупроводника, создают в пределах этой зоны дискретные энергетические уровни либо у нижнего ее края вблизи к ВЗ, либо – у верхнего, вблизи к 3П (см. рис. ___, б, в). Вследствие своей малой концентрации атомы примеси располагаются в решетке полупроводника на очень больших расстояниях друг от друга, поэтому между собой не взаимодействуют.
Лабораторная работа № 9
ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ ПОЛУПРОВОДНИКОВ
9.1. Цель работы
Изучить зависимость сопротивления полупроводника от температуры. Научиться определять энергию активации полупроводников в джоулях по зависимости ln от обратной температуры 1/T.
9.2. Задачи работы
1. Для исследуемых образцов определить температурные коэффициенты сопротивления ТКR.
2. Вычислить энергию активации полупроводников для исследуемых образцов.
9.3. Краткие теоретические сведения
При температуре 0 К и в отсутствие другого энергетического воздействия все валентные электроны полупроводника находятся на энергетических уровнях ВЗ. В этом состоянии полупроводник подобен диэлектрику и его проводимость равна нулю. Для переброса электронов из ВЗ в ЗП нужна дополнительная энергия для преодоления потенциального барьера в виде 33. При температуре большей 0 К и дальнейшем ее повышении электроны под действием тепловой энергии начнут переходить в ЗП; в результате образуются пары свободных носителей заряда – электроны в ЗП, а дырки – в ВЗ. Этот процесс называют тепловой генерацией свободных носителей заряда. В ЗП (благодаря наличию свободных уровней) электроны под действием приложенного электрического поля будут перемещаться с уровня на уровень, образуя электрический ток. Аналогично в ВЗ дырки образуют электрический ток. Одновременно с тепловой генерацией свободных носителей заряда существует и обратный процесс, когда свободный электрон возвращается в незаполненную ВЗ. Этот процесс называется рекомбинацией электрона с дыркой. При заданной температуре между этими процессами осуществляется термодинамическое равновесие, в результате чего в ЗП устанавливается некоторая, вполне определенная концентрация свободных электронов, а в ВЗ – дырок проводимости.
В примесных полупроводниках переходы электронов из ВЗ полупроводника на уровни акцепторной примеси и с локальных уровней донорной примеси в ЗП полупроводника осуществляются при более низких затратах энергии, чем переход электронов из ВЗ собственного полупроводника в его ЗП, т. е. W > Wа (Wд ). Поэтому электропроводность примесных полупроводников начинает проявляться при более низких температурах, чем электропроводность собственных полупроводников.
Вероятность переходов носителей заряда на свободные уровни энергии и, следовательно, величина электропроводности сильно возрастают с ростом температуры. Зависимость удельной электропроводности от температуры в общем виде выражается экспоненциальной функцией:
![]() ,
,
где А – постоянная величина; W – ширина 33, эВ; k – постоянная Больцмана, равная 1,38 10–23 Дж/К; Т – абсолютная температура.
Для полупроводников с одним типом носителей заряда удельная электропроводность , См/м, определяется тем же выражением:
= n q a, (9.1)
где п – концентрация свободных носителей заряда, м–3; q – величина заряда каждого из них, Кл; а – их подвижность – отношение дрейфовой скорости V свободных носителей заряда к напряженности Е электрического поля, вызвавшего дрейфовую скорость (а = V/E, [(м/с)/(В/м) = м2/(В с)]). Поскольку подвижность а носителя заряда имеет тот же знак, что и его заряд q, удельная электропроводность , получаемая из формулы (9.1), всегда будет положительной независимо от знака заряда.
В широком интервале температуры концентрация свободных носителей заряда п и их подвижность а изменяются по различным законам. Поэтому зависимость удельной электропроводности примесных полупроводников от обратной температуры в широком интервале имеет сложный характер. В общем виде эта зависимость представлена на рис. 9.1, на котором видны области примесной электропроводности пр (участок АБ) и собственной соб (участок ВГ). При этом = соб + пр.
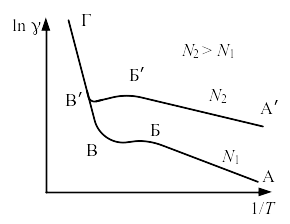
Рис. 9.1. Температурная зависимость удельной электропроводности примесного полупроводника с различной концентрацией N примеси: АБ и А'Б' – участки, характеризующие примесную электропроводность; ВГ – участок, характеризующий собственную электропроводность; БВ и Б'В' – области насыщения.
Собственную электропроводность и примесную можно опреде лить с помощью следующих уравнений:
![]() , (9.2)
, (9.2)
![]() , (9.3)
, (9.3)
где A – постоянная величина; k – постоянная Больцмана; Т – абсолютная температура. Уравнение (9.3) справедливо, пока не наступит полная ионизация примеси.
Таким образом, собственная и примесная электропроводности полупроводниковых материалов с ростом температуры возрастают, т.е. они обладают отрицательным коэффициентом сопротивления.
Прологарифмировав уравнения (9.2) и (9.3), получим:
![]() ,
,
![]() .
.
Из выражений (9.3, 9.3) получаем выражение для удельного сопротивления полупроводника