Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	математика

дисциплине

Выполнил(а) студент(ка)
			фамилия имя отчество
Идентификационный номер:		2009-1201-8

Пермь 2021

Задание № 2. Найти производные функций.



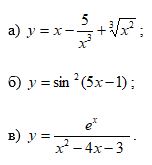
А)



Б)

1. 
   Заменим u=sin(5x−1)u=sin⁡(5x−1).
   
2. 
   В силу правила, применим: u2u2 получим 2u2u
   
3. 
   Затем примените цепочку правил. Умножим на ddxsin(5x−1)ddxsin⁡(5x−1):
   
   1. 
      Заменим u=5x−1u=5x−1.
      
   2. 
      Производная синуса есть косинус:
      

ddusin(u)=cos(u)ddusin⁡(u)=cos⁡(u)

3. 
   Затем примените цепочку правил. Умножим на ddx(5x−1)ddx(5x−1):
   
   1. 
      дифференцируем 5x−15x−1 почленно:
      
      1. 
         Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
         
         1. 
            В силу правила, применим: xx получим 11
            

Таким образом, в результате: 55

2. 
   Производная постоянной −1−1 равна нулю.
   

---

В результате: 55

4. 
   В результате последовательности правил:
   
5. 
   5cos(5x−1)5cos⁡(5x−1)
   
1. 
   В результате последовательности правил:
   
2. 
   10sin(5x−1)cos(5x−1)10sin⁡(5x−1)cos⁡(5x−1)
   
3. 
   Теперь упростим:
   

5sin(10x−2)5sin⁡(10x−2)

Ответ: 5sin(10x−2)

В)

1. 
   Применим правило производной частного:
   

ddxf(x)g(x)=−f(x)ddxg(x)+g(x)ddxf(x)g2(x)ddxf(x)g(x)=−f(x)ddxg(x)+g(x)ddxf(x)g2(x)

f(x)=exf(x)=ex и g(x)=x2−4x−3g(x)=x2−4x−3.

Чтобы найти ddxf(x)ddxf(x):

1. 
   Производная exex само оно.
   

Чтобы найти ddxg(x)ddxg(x):

2. 
   дифференцируем x2−4x−3x2−4x−3 почленно:
   
   1. 
      Производная постоянной −3−3 равна нулю.
      
   2. 
      В силу правила, применим: x2x2 получим 2x2x
      
   3. 
      Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
      
      1. 
         В силу правила, применим: xx получим 11
         

Таким образом, в результате: −4−4

3. 
   В результате: 2x−42x−4
   

Теперь применим правило производной деления:

−(2x−4)ex+(x2−4x−3)ex(x2−4x−3)2−(2x−4)ex+(x2−4x−3)ex(x2−4x−3)2

2. 
   Теперь упростим:
   

(x2−6x+1)ex(−x2+4x+3)2(x2−6x+1)ex(−x2+4x+3)2

Ответ:

(x2−6x+1)ex(−x2+4x+3)2

Задание № 3. Составить уравнение касательной к графику функции  y=x³–4x+3 в точке x=2

Ответ: у=8х–13.

Решение:

y=x³–4x+3, х₀=2.
Переобозначим функцию: f(x)=x³–4x+3.
Уравнение касательной имеет вид:
y=f(x₀)+f'(x₀)(x–x₀).
Вычисляем:
f(x₀)=f(2)=2³–4·2+3=8–8+3=3,
f'(x)=3x²–4,
f'(x₀)=f'(2)=3·2²–4=12–4=8.
Составляем уравнение касательной:
у=3+8(х–2),
у=3+8х–16,
у=8х–13.
Задание № 4. Вычислить неопределенные интегралы.

 

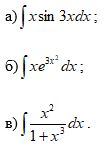
Ответ:

А)

1. 
   Рассмотрим интеграл ∫(x * sin(3 * x))dx, которого обозначим через А. Применим формулу интегрирования по частям: ∫u(x)dv(x) = u(x) * v(x) - ∫v(x)du(x). Положим u = x, dv = sin(3 * x) dx. Тогда: du = dx и v = -(1/3) * cos(3 * x).
   
2. 
   Поэтому A = ∫(x * sin(3 * x))dx = -(1/3) * x * cos(3 * x) - ∫(-(1/3) * cos(3 * x))dx = -(x / 3) * cos(3 * x) + (1/3) * ∫cos(3 * x)dx.
   
3. 
   Легко вычисляется интеграл ∫cos(3 * x)dx = (1/3) * sin(3 * x) + С. Следовательно, А = -(x / 3) * cos(3 * x) + (1/9) * sin(3 * x) + С.
   

---

Ответ:  -(x / 3) * cos(3 * x) + (1/9) * sin(3 * x) + С.
Б)


Выражение 2*x подведем под знак дифференциала, т.е.:
2·x·dx = d(x²), t=x²
Тогда исходный интеграл можно записать так:

Это табличный интеграл:

Чтобы записать окончательный ответ, осталось вместо t подставить x^2.


В)


Выражение 3*x^2 подведем под знак дифференциала, т.е.:
3·x²·dx = d(x³), t=x³
Тогда исходный интеграл можно записать так:


Вычисляем табличный интеграл:

Ответ:

или
ln((x+1)^1/3) + C
Чтобы записать окончательный ответ, осталось вместо t подставить x^3.


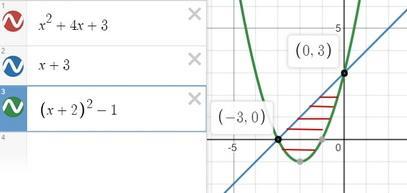
 Задание № 5. Вычислить площадь фигуры, ограниченной линиями y = x² + 4x + 3  и y = x + 3. Построить график.

Ответ:

9/2

Пошаговое объяснение:

Сначала чертим графики

y = х² + 4x + 3

Выделим полный квадрат  х² + 4x + 3 = (х² +2*2х +4) -4 +3 = (х+2)² -1

---

значит, берем известный график функции у = х²,

смещаем его на -2 по оси ОХ и на -1 по оси ОУ.

y = x + 3

берем известный график у = х и смещаем его на -3 по оси ОХ.

Вот мы получили нужную нам фигуру.

Теперь по формуле Ньютона - Лейбница вычислим определенный интеграл, что и будет площадью фигуры

   , где

х ∈ [a; b] ;    за у₁(х) принимают функцию, график которой лежит "выше" на отрезке  [a; b]

Для нашего случая

---

Смотрите также файлы

• Индивидуальные траектории профессионального развития (тест с ответами Синергиямои мти мосап).docx

• Рабочая программа воспитания 20222027 год (входит в состав ооп ноо, ооо, соо) п. Мамакан, 2022 2 содержание.pdf

• Контрольная работа решение задач методом бесконечного цепного повтора (Вариант 20) Студент.docx

• Организационная культура.ppt

• Эндоскопическая хирургия, 5, Синдром ПрадераВилли (спв).pdf