Файл: Занятие 12 и 13. Проектирование логических схем с помощью функций алгебры логики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема Основные логические элементы
Практическое занятие № 12 и 13. Проектирование логических схем с помощью функций алгебры логики
Цель занятия: ПОСТРОЕНИЕ ФУНКЦИОНАЛЬНЫХ СХЕМ на базе элементарных логических элементов
Порядок выполнения отчета по практической работе №4
1. Ознакомиться с теоретическим материалом по практической работе.
2. Записать краткий конспект теоретической части.
3. Выполнить задание по практической работе согласно варианту.
4. Продемонстрировать результаты выполнения заданий преподавателю.
5. Записать выводы о проделанной работе.
6. Подготовить отчет по практической работе с ответами на контрольные вопросы и результатами проделанной работы.
Краткие теоретические материалы по теме практического занятия
Логическая схема цифрового устройства (в том числе и цифрового автомата) строится на основе объединения электронных элементов. Эти элементы реализуют конкретные логические и математические операции и носят название ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ. На вход каждого элемента подаются сигналы, называемые входными. На выходе получаем выходной сигнал. Если есть сигнал – значит, он равен 1, если нет сигнала – равен 0. Каждая логическая схема реализует определенную логическую функцию, и при подаче на ее вход строго определенной комбинации входных сигналов мы должны получить на выходе вполне определенный результат — 0 или 1.
Принципы работы цифровых автоматов в своей основе весьма просты. Их работа состоит в операциях над числами и символами, закодированными двумя цифрами – 0 и 1. А работа всех устройств компьютера заключается в операциях над этими последовательностями из 0 и 1. Существуют различные физические способы кодирования двоичной информации. В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули, например, уровню сигнала 5 вольт соответствует логическая 1, а уровню 0 вольт соответствует логический-0:
Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Логическая схема отображает процесс вычисления логической формулы, заключающийся в определенной последовательности выполнения логических операций. Каждый отдельный блок логической схемы, обозначающий логическую операцию, называется логическим элементом. Этим элементам присвоены следующие названия:
• логический элемент И — конъюнктор: осуществляет конъюнкцию — логическое умножение;
• логический элемент ИЛИ — дизъюнктор: осуществляет дизъюнкцию — логическое сложение;
• логический элемент НЕ — инвертор: осуществляет инверсию —логическое отрицание.
Схемные элементы ЭВМ
Электронные цифровые схемы формально можно разделить на 2 класса:
1. Комбинационные схемы (КС) – не обладают памятью. Выходной сигнал формируется в зависимости от комбинации входных данных в фиксированный момент времени (учитывая задержку на преобразования сигналов), в качестве примеров можно привести следующие функциональные узлы компьютера: Управляемые шины, мультиплексоры и демультиплексоры, дешифраторы и шифраторы, преобразователи кодов, комбинационные счетчики и сумматоры и т. д. 2. Схемы с памятью – алгоритм их работы зависит от состояния входов и памяти (того, что было в предыдущие моменты времени). Например, триггер. Эти схемы описываются с применением теории конечных автоматов.
Другими словами первый класс — логические устройства, обрабатывающие входной сигнал. Второй - элементы обладающие памятью и реагирующие на сигнал в зависимости от введенных в них данных.
Логические операции и базовые элементы компьютера
Преобразование информации в ВМ осуществляется элементами (схемами) двух классов:
• комбинационными;
• последовательностными (схемами с памятью).
Состояние выходов к о м б и н а ц и о н н ы х схем однозначно определяется состояниями входов в данный момент времени.
Состояние выходов в п о с л е д о в а т е л ь н о с т н ы х схемах определяется
не только состоянием входов, но и внутренними состояниями, имевшими место в предыдущие моменты времени.
Комбинационные схемы являются техническим аналогом булевых функций. Подобно тому, как сложная булева функция может быть получена суперпозицией более простых функций, так и комбинационная схема может строиться из более простых схем.
Логический элемент процессора (ЦА) — это часть электронной схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-HE» или другие (называемые также вентилями), а также триггер. Можно показать, что с помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Работу логических элементов описывают с помощью таблиц истинности.
Рассмотрим логические операции и соответствующие им элементы логических схем.
Конъюнкция. Соединение двух (или нескольких) высказываний в одно с помощью союза «И» называется операцией логического умножения, или конъюнкцией. Эту операцию принято обозначать знаками « ^ , &» или знаком умножения « х » . Сложное высказывание А и В истинно только в том случае, когда истинны оба входящих в него высказывания. (см. Практическое занятие № 1).
Л о г и ч е с к а я схема «И» реализует конъюнкцию двух или более логических значений. Условное обозначение на схеме для 2 входных переменных:
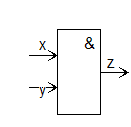
Единица на выходе схемы «И» будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль. Связь между выходом z этой схемы и входами х и у описывается соотношением z = x & у (читается как «х и у»). Операция конъюнкции на структурных схемах обозначается знаком «&».
Дизъюнкция. Объединение двух (или нескольких) высказываний с помощью союза или (or) называется операцией логического сложения, или дизъюнкцией. Эту операцию обозначают знаками «| , v» или знаком сложения «+». Сложное высказывание A v В истинно, если истинно хотя бы одно из входящих в него высказываний (см.
Практическое занятие № 1). Л о г и ч е с к а я схема «ИЛИ» реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы «ИЛИ» будет единица, на ее выходе также будет единица. Условное обозначение на структурных схемах схемы «ИЛИ» с двумя входами представлено на рис.
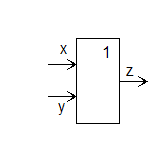. Знак «1» на схеме происходит от классического обозначения дизъюнкции как «>» (т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами х н у описывается соотношением z = x v у.Работа элемента ИЛИ предполагает, что сигнал 1 на выходе будет получен, если сигнал 1 поступает хотя бы на один вход: либо на Х, либо на Y, либо и на Х и на Y одновременно. Сигнал 0 на выходе элемента ИЛИ появляется только в том случае, если сигнал 1 не поступил ни на один вход.
Исключающее ИЛИ( XOR) – операция, которая принимает значение «истина» только если всего один из аргументов имеет значение «истина».
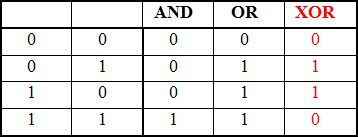
XOR обладает следующими свойствами:
a XOR 0 = a
a XOR a = 0
a XOR b = b XOR a
(a XOR b) XOR b = a
Процесс построения функциональных схем для разработки устройств ПК можно описать следующим образом:
1. На основании анализа функции, которую реализует устройство, составляется таблица истинности.
2. По этой таблице находят логическую функцию.
а) в заданной таблице выбираются наборы переменных, при которых значение функции равно 1.
б) для каждого такого набора записываются конъюнкции всех входных переменных, имеющих значение 1. При этом те переменные, которые имеют значение 0, записываются с отрицанием.
в) все полученные конъюнкции объединяются знаками дизъюнкции. Это и будет искомая логическая функция, которую предстоит далее упростить.
3. Производится упрощение логической функции.
4. По упрощённой логической функции строится функциональная логическая схема устройства.
5. При построении логической схемы необходимо учитывать установленные в алгебре логики правила (приоритеты) для выполнения логических операций, которые в данном случае реализуются с помощью логических элементов НЕ, И и ИЛИ. Порядок производимых логических операций будет следующий: операция инверсии (отрицания), операция логического умножения (конъюнкции) и затем операция логического сложения (дизъюнкции).
В качестве примера ниже представлена схема электрическая функциональная логического преобразователя (комбинационного автомата), реализующего логическую функцию
в элементном базисе из логических элементов И, ИЛИ, НЕ. 
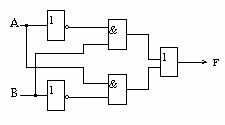
Способы задания логических функций
В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функций). Для описания функций алгебры логики могут быть использованы различные способы. Основными из них являются описание функций в словесной форме, в виде таблиц истинности и алгебраических выражений.
Проиллюстрируем словесное описание функции алгебры логики на примере.
Логическая функция трех переменных равна 1, если хотя бы две входные переменные равны 1.
Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства.
Таблица, содержащая все возможные комбинации входных переменных xn-1 …x1x0 и соответствующие им значения выходных переменных yi, называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2n строк и m+n столбцов, где n – количество входных сигналов, а m – выходных.
При описании функций алгебры логики алгебраическим выражением используются две стандартные формы ее представления – так называемые дизъюнктивная и конъюнктивная нормальные формы.
Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз.
ДНФ может быть получена из таблицы истинности с использованием следующего алгоритма:
а) для каждого набора переменных, на котором функция алгебры логики равна единице, записывают элементарные логические произведения входных переменных, причем переменные, равные нулю, записывают с инверсией. Полученные произведения называют конституентами единицы;
б) логически суммируют все конституенты единицы.