Файл: Занятие 12 и 13. Проектирование логических схем с помощью функций алгебры логики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 72
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ДНФ, полученную суммированием конституент единицы, называют совершенной (СДНФ).
Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входят один раз.
КНФ может быть получена из таблицы истинности с использованием следующего алгоритма:
а) для каждого набора переменных, на котором функция алгебры логики равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля;
б) логически перемножают все полученные конституенты нуля.
КНФ, полученную суммированием конституент нуля, также называют совершенной (СКНФ).
Пример 1.1.Запишите дизъюнктивную и конъюнктивную нормальные формы для следующей таблицы истинности:
| x2 | x1 | x0 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Решение. Согласно приведенному выше алгоритму дизъюнктивная нормальная форма примет вид
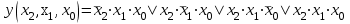, (1.1)а конъюнктивная нормальная форма определится как
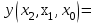
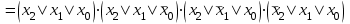. (1.2)Иногда удобнее применять не саму функцию алгебры логики, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать нулевые, а для записи СКНФ – единичные значения функции.
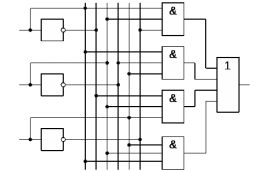
Рис. 1. Пример структурной схемы логического устройства
Варианты заданий
Синтезировать логическую схему, реализующую следующие логические функции.
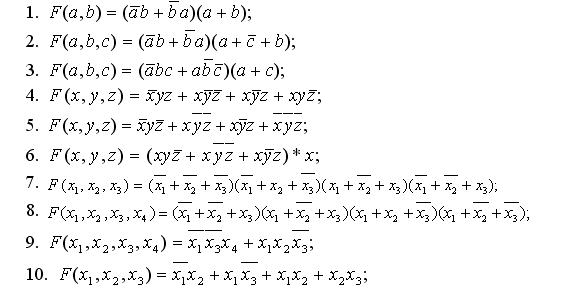
11.
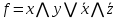
12.
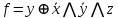
13.
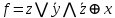
Варианты заданий (продолжение)
1.
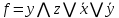
2.
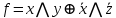
3.
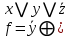)4.
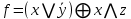
5.
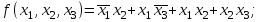
6.
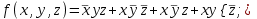
7.
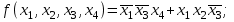
8.
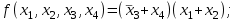
9.
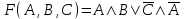
10.
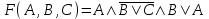
11.
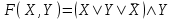
12.
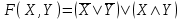
13.
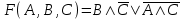
Контрольные вопросы:
3.1 Что такое логическая схема?
3.2 По каким принципам можно классифицировать логические схемы?
3.3 Что такое логические операторы?
3.4 Таблица истинности логических операций:
a ∧ b; a ∨ b; a → b; a = b; a ⊕ b.
3.5. Условное графическое обозначение (УГО) базовых логических элементов.
3.6. Напишите основные Законы алгебры логики.
3.7. Алгоритм построения логической функции по ее таблице истинности
Примечание. Для графического отображения логических схем существуют различные компьютерные программы, называемые графическими редакторами. Данные программы могут быть включены в другие компьютерные программы, например в программах Microsoft Word и Microsoft Excel такие редакторы реализованы с помощью панелей инструментов «Рисование», или быть самостоятельными программами, например Paint, Microsoft Visio и т. д.