Файл: Методические указания к выполнению контрольной работы по дисциплине Дискретная математика для обучающихся 2 курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 101
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 x2 x4 x3)
А и В содержат одинаковый сомножитель (подчеркнуты). Поэтому осуществляет операцию приведения подобных членов: в А или В заменяем его на 1 или, что то же самое, вычеркиваем его из А или из В.
Окончательно имеем с.к.н.ф.
F = АВ= (x1 x3 x2 x4) (x1 x3 x2 x4) (x1 x2 x4 x3).
Глава 4. РАСПОЗНАЮЩИЕ КОНЕЧНЫЕ АВТОМАТЫ
Распознающими конечными автоматами являются конечные автоматы, результатом работы которых является обнаружение некоторого свойства в заданном тексте. Обработку произвольного слова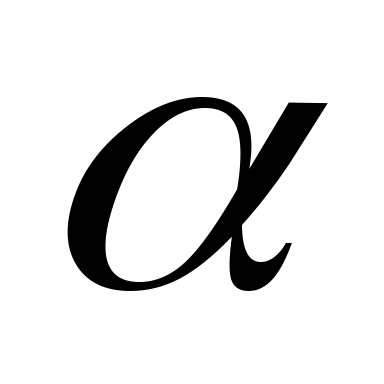 во входном алфавите
во входном алфавите  автомат начинает из специально выделенного начального состояния. В каждый такт дискретного времени на вход автомата поступает очередная буква обрабатываемого слова, под ее воздействием автомат меняет свое состояние; состояние в которое автомат перейдет, определяется предыдущим его состоянием и прочитанной буквой входного слова. Над словом длины
автомат начинает из специально выделенного начального состояния. В каждый такт дискретного времени на вход автомата поступает очередная буква обрабатываемого слова, под ее воздействием автомат меняет свое состояние; состояние в которое автомат перейдет, определяется предыдущим его состоянием и прочитанной буквой входного слова. Над словом длины 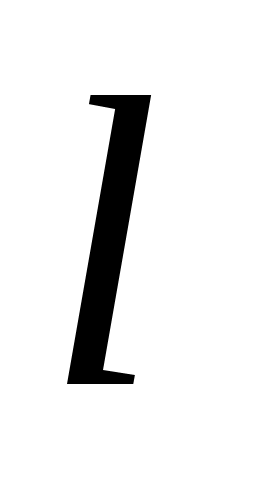 автомат работает
автомат работает 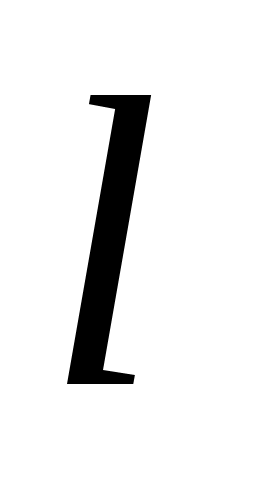 тактов. Результат работы автомата определяется состоянием, в котором он оказывается по ее завершении.
тактов. Результат работы автомата определяется состоянием, в котором он оказывается по ее завершении.
Формально конечный автомат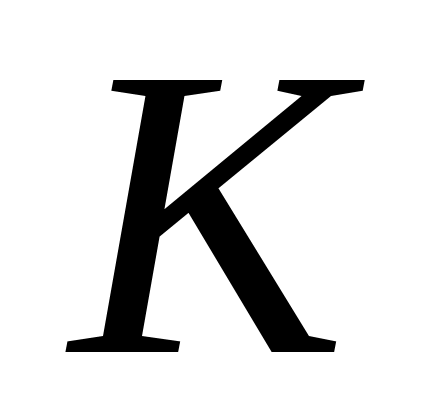 определяется как совокупность
определяется как совокупность
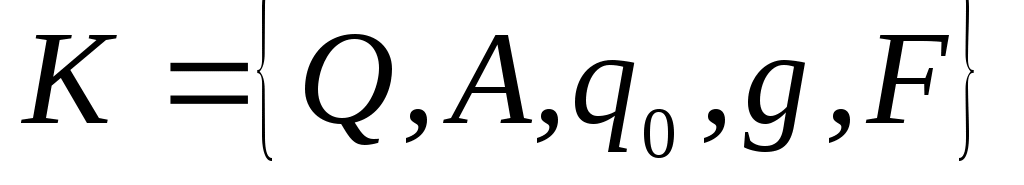 ,
,
где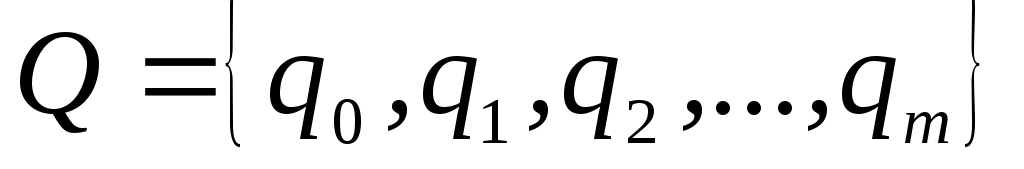 – множество состояний автомата;
– множество состояний автомата;  – входной алфавит;
– входной алфавит; 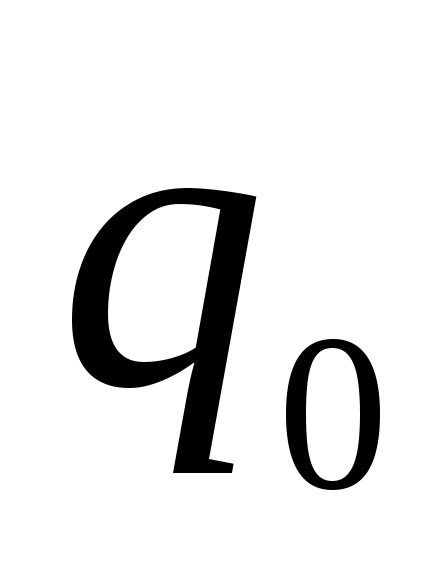 – специально выделенное состояние автомата, именуемое начальным состоянием;
– специально выделенное состояние автомата, именуемое начальным состоянием; 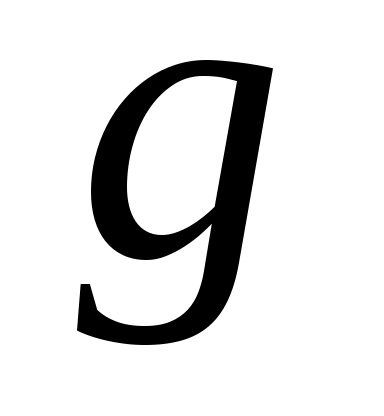 – функция переходов конечного автомата, представляющая собой отображение типа
– функция переходов конечного автомата, представляющая собой отображение типа 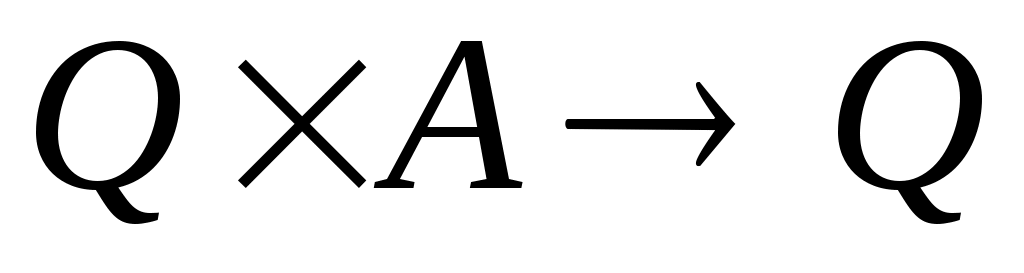 (если
(если 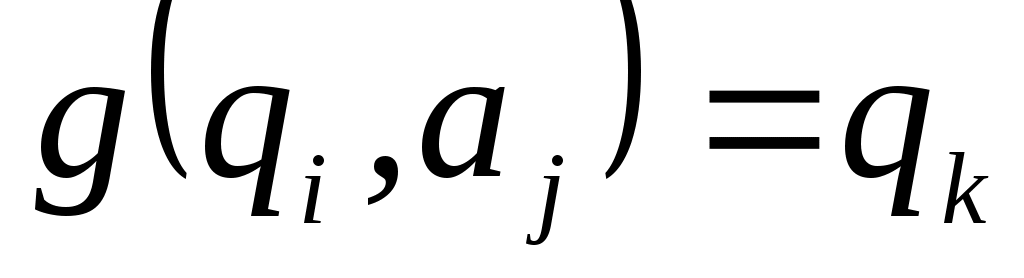 , то автомат из состояния
, то автомат из состояния 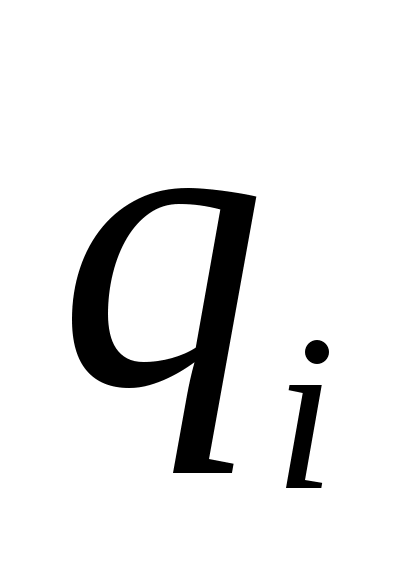 под воздействием буквы
под воздействием буквы  должен перейти в состояние
должен перейти в состояние 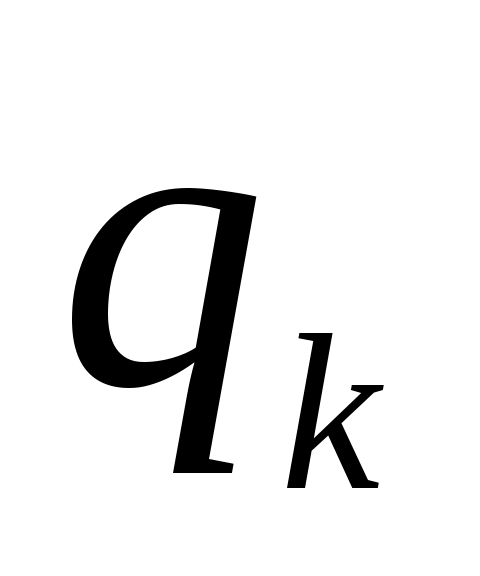
);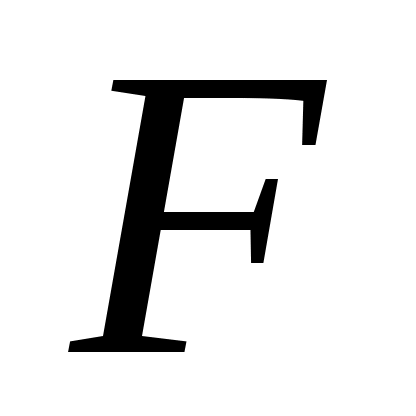 – специально выделенное подмножество состояний автомата, которые условно называются «хорошими»,
– специально выделенное подмножество состояний автомата, которые условно называются «хорошими»,  . (соответственно «плохими» называются состояния из множества
. (соответственно «плохими» называются состояния из множества 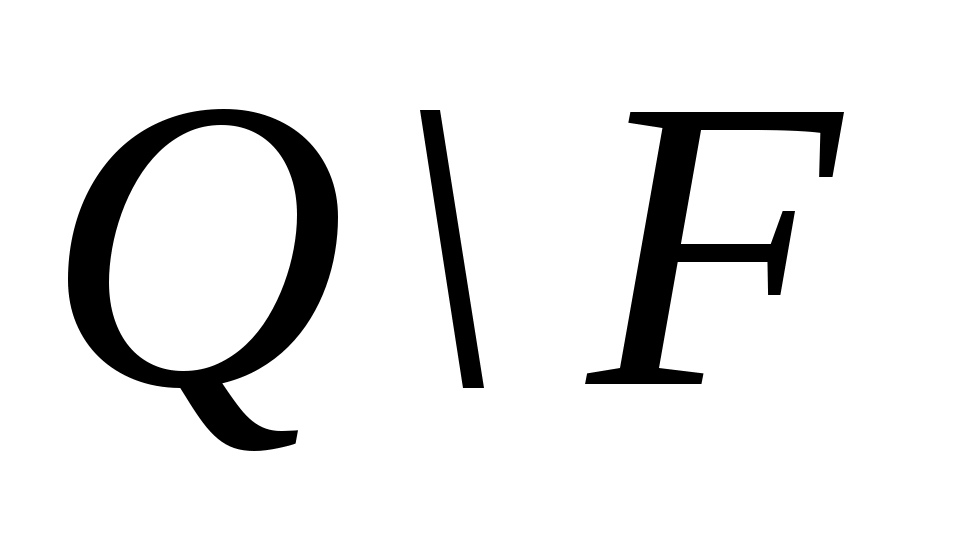 ).
).
Пусть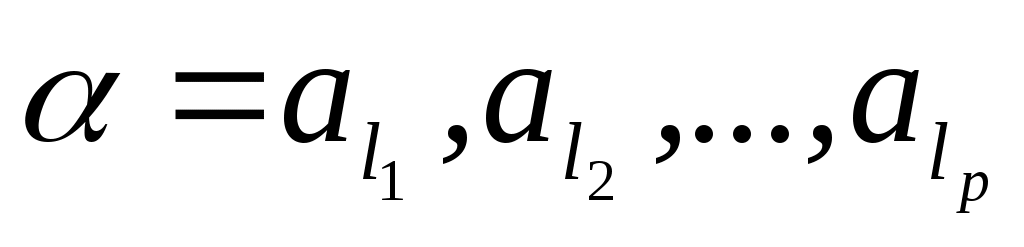 – входное слово,
– входное слово, 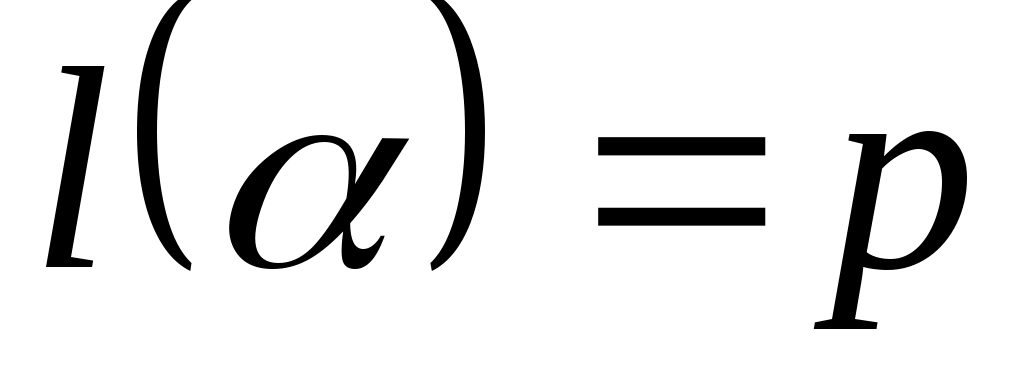 . Через
. Через 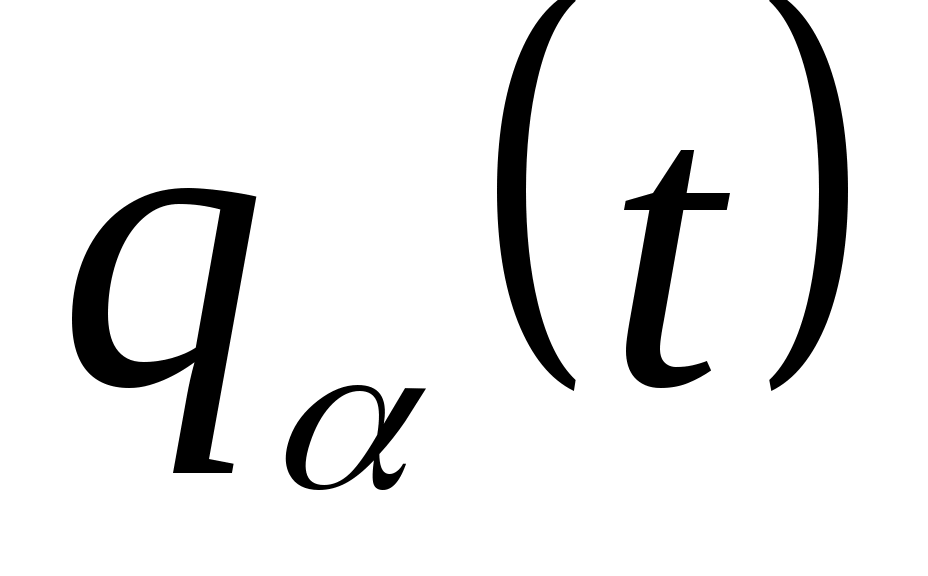 обозначим состояние, в котором оказывается автомат
обозначим состояние, в котором оказывается автомат  через
через 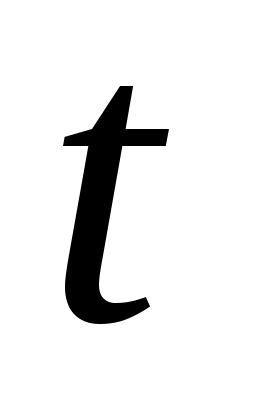 тактов работы над этим словом (здесь
тактов работы над этим словом (здесь 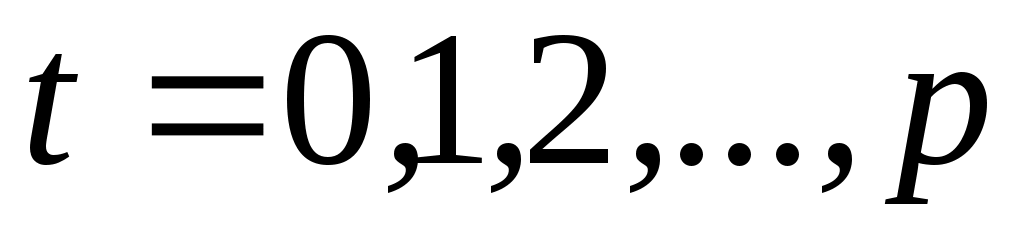 ):
): 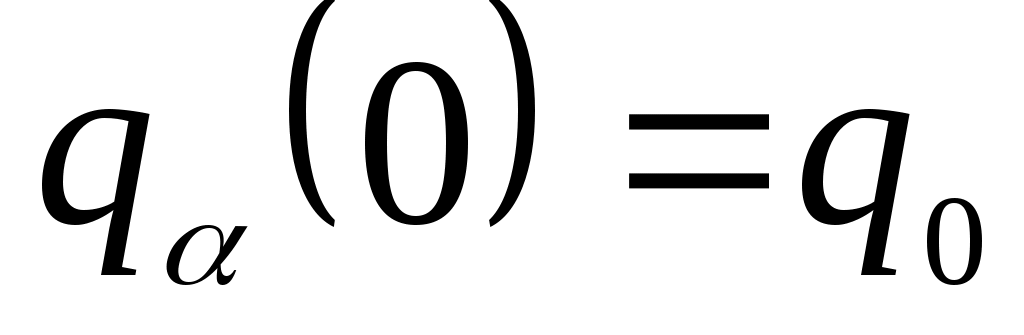 ,
, 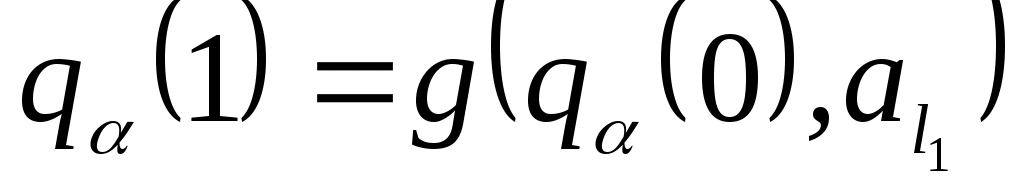 ,
, 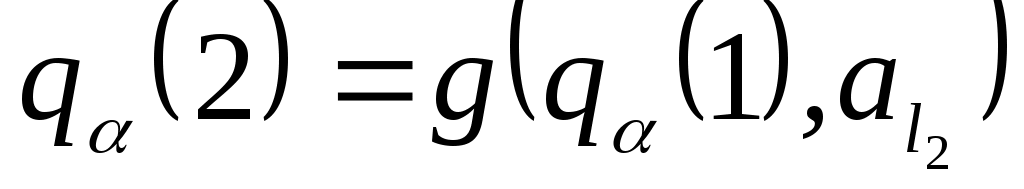 , …,
, …, 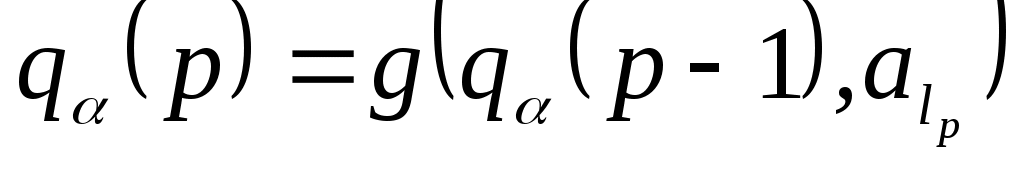 .
.
Слово принимается автоматов
принимается автоматов  , если
, если 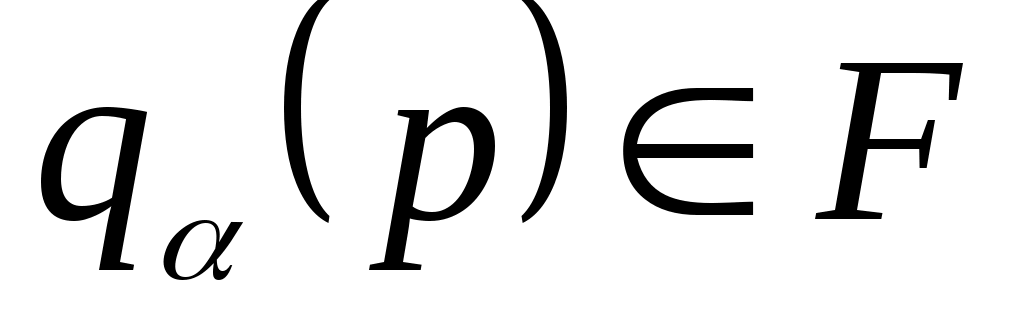 . Введем в рассмотрение язык
. Введем в рассмотрение язык 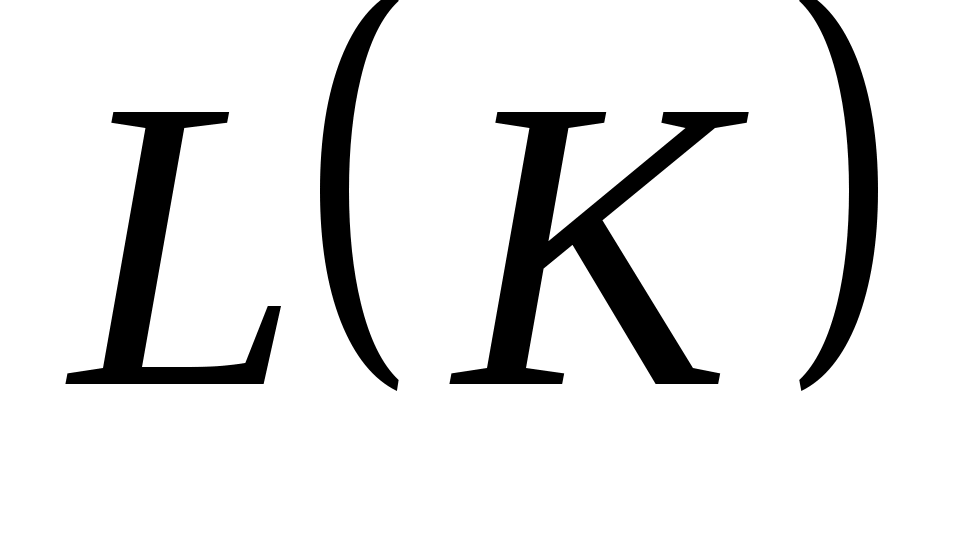 : слово
: слово  принадлежит языку
принадлежит языку 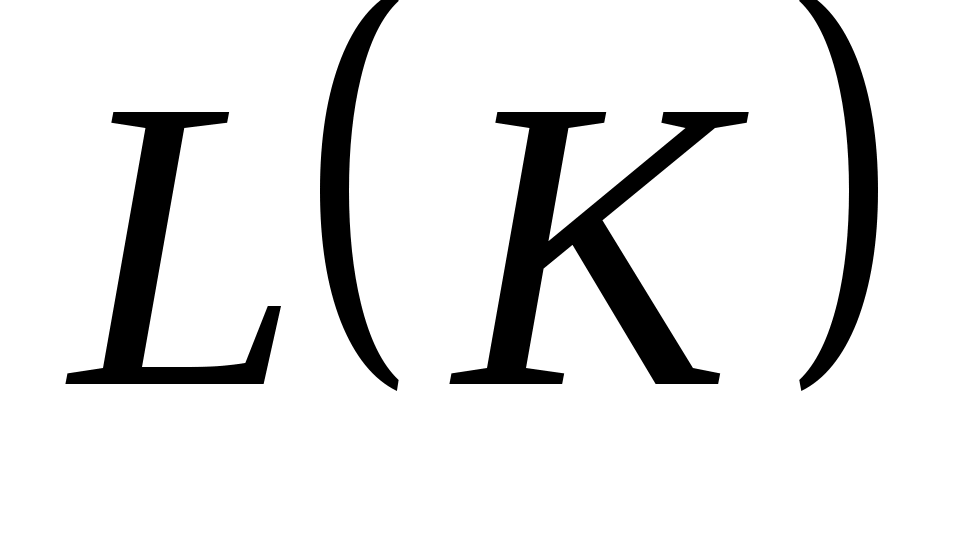 , если данное слово принимается автоматом
, если данное слово принимается автоматом  . Язык
. Язык 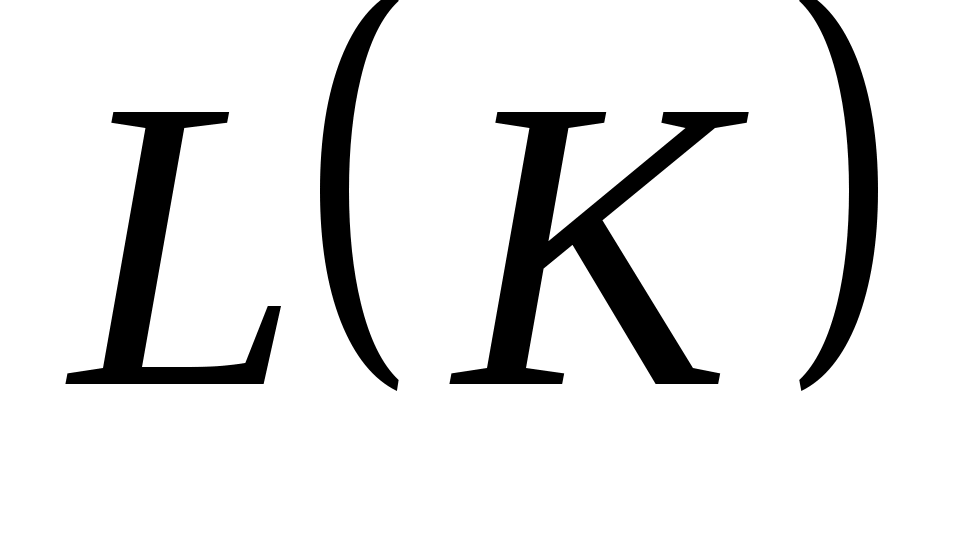 называется языком, распознаваемым данным конечным автоматом.
называется языком, распознаваемым данным конечным автоматом.
Определение 1. Язык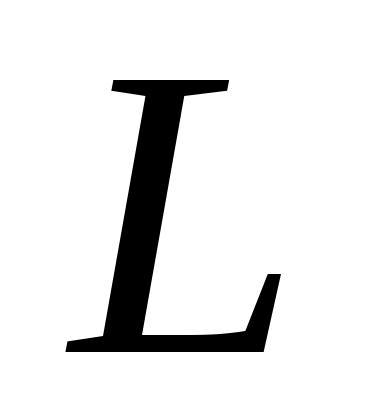 называется регулярным, если для него можно построить распознающий конечный автомат.
называется регулярным, если для него можно построить распознающий конечный автомат.
Конечный автомат удобно задавать диаграммой его переходов. Диаграмма представляет собой ориентированный граф, вершины которого одноименны состояниям автомата; дуга из вершины в вершину
в вершину  с надписанной над ней буквой
с надписанной над ней буквой  проводится тогда и только тогда, когда
проводится тогда и только тогда, когда  . В случае, когда переход из
. В случае, когда переход из  в
в  осуществляется под воздействием любой из букв некоторого подмножества
осуществляется под воздействием любой из букв некоторого подмножества 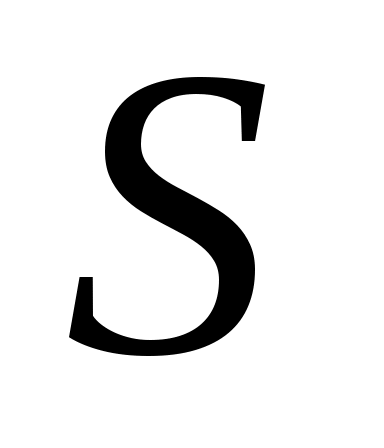 ,
, 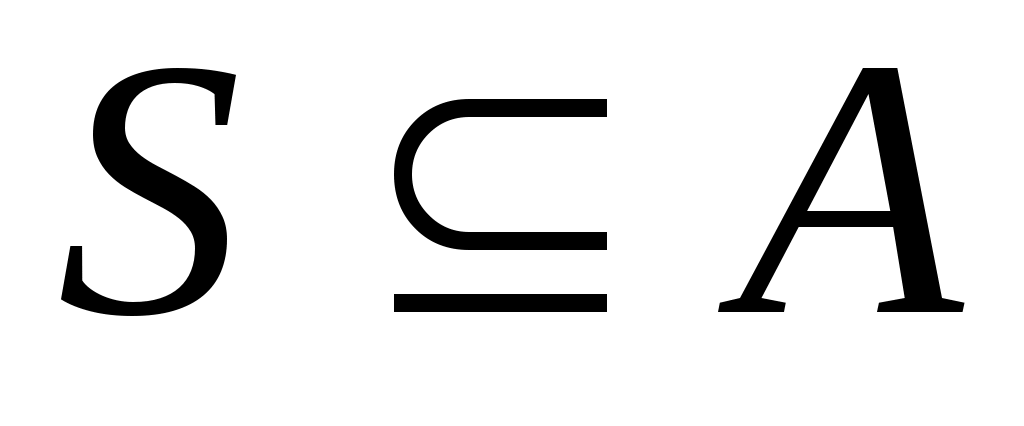 , все буквы этого подмножества подписываются над соответствующей дугой (вместо перечня всех букв допускается сокращенная запись «
, все буквы этого подмножества подписываются над соответствующей дугой (вместо перечня всех букв допускается сокращенная запись «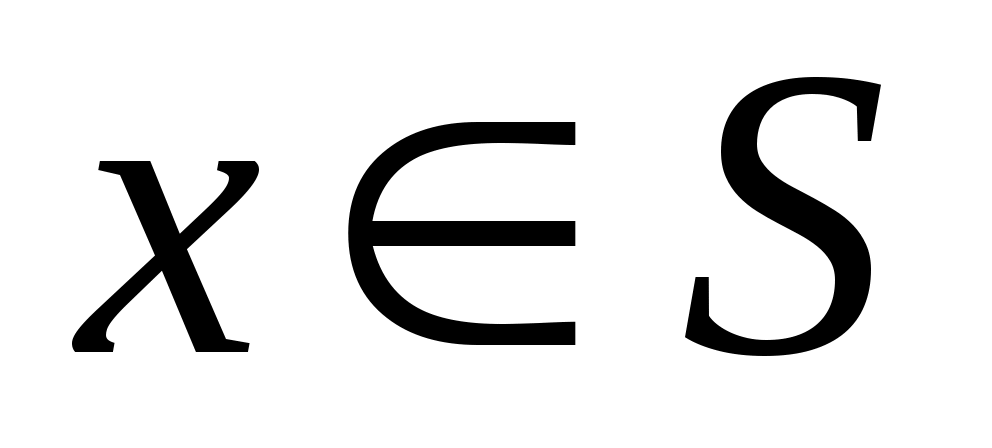 » или «
» или «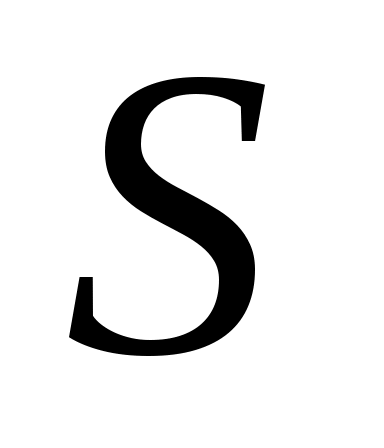 ». Если произвольное состояние
». Если произвольное состояние  входит в
входит в  , то данный факт на диаграмме отмечается жирным кружком, выделяющим вершину
, то данный факт на диаграмме отмечается жирным кружком, выделяющим вершину  .
.
На рис.1 примера 1 показана диаграмма автомата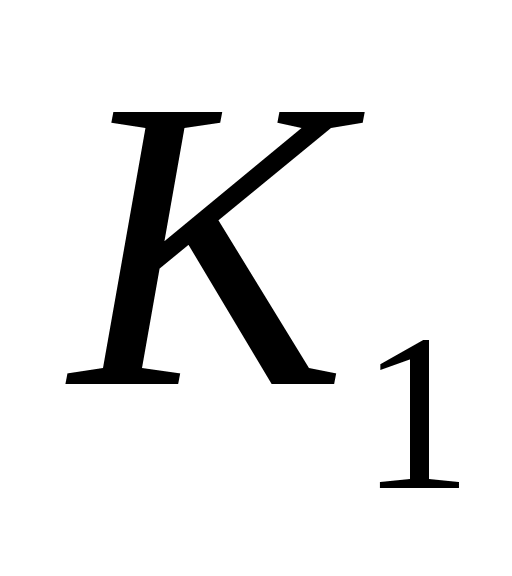 , работающего над словами алфавита
, работающего над словами алфавита 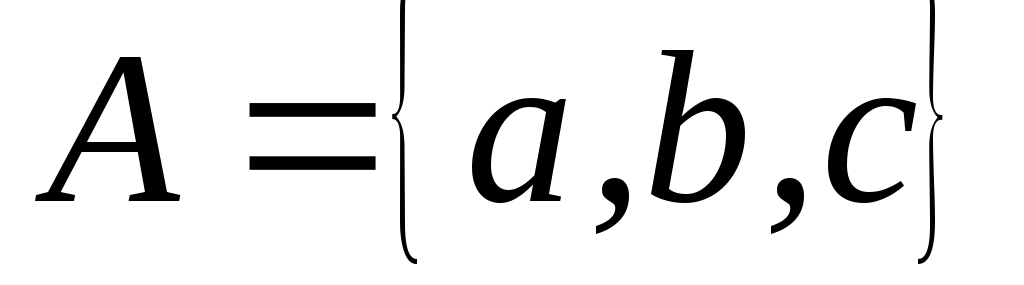 . Автомат имеет два состояния:
. Автомат имеет два состояния:  и
и 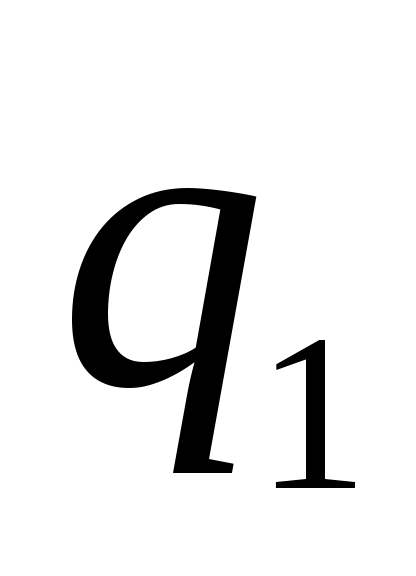 , причем «хорошим» является только состояние
, причем «хорошим» является только состояние 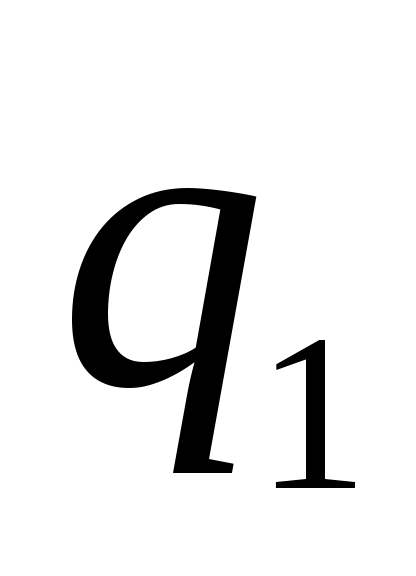 . Начав работу в состоянии
. Начав работу в состоянии  , автомат под воздействием букв
, автомат под воздействием букв 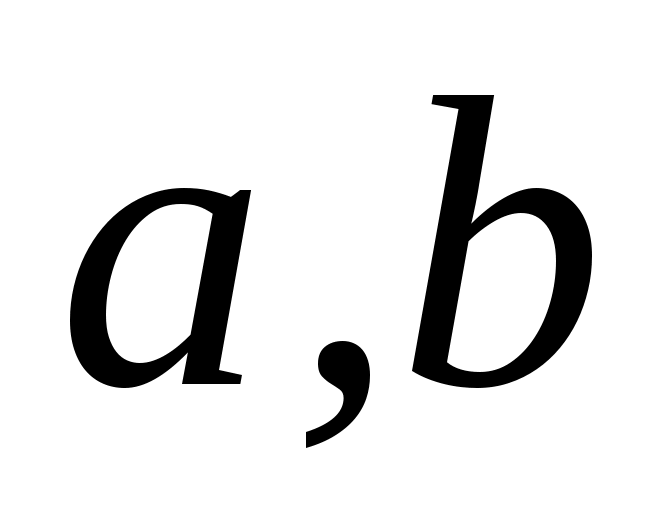
из этого состояния не выходит; под воздействием буквы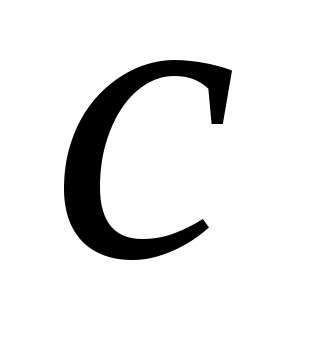 реализуется переход в состояние
реализуется переход в состояние  ; любая далее поступающая буква оставляет автомат в том же состоянии. Таким образом, автомат
; любая далее поступающая буква оставляет автомат в том же состоянии. Таким образом, автомат  распознает язык
распознает язык 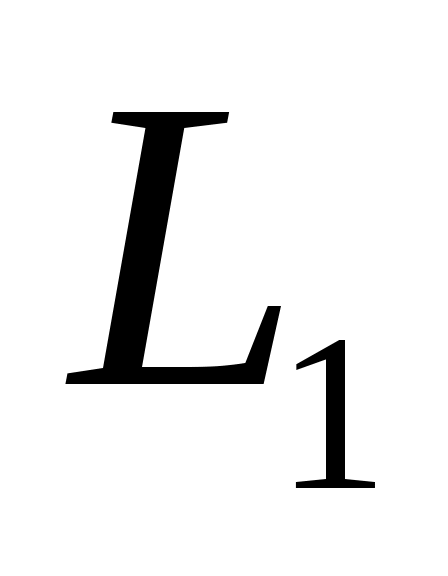 , состоящий из слов, имеющих в своем составе букву
, состоящий из слов, имеющих в своем составе букву 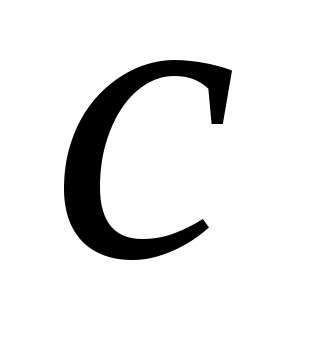 .
.
П ример 1.
ример 1.
Рисунок 1.
Класс регулярных языков замкнут относительно основных теоретико-множественных операций – объединения, пересечения, разности.
Пусть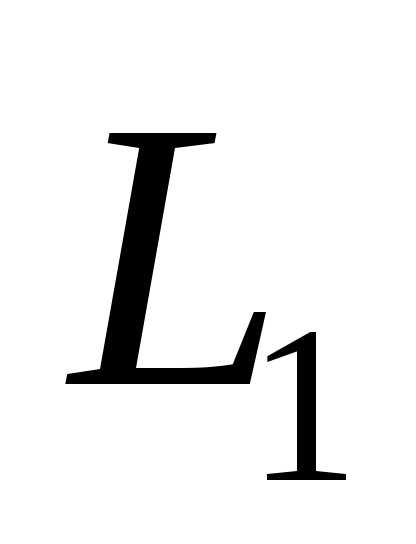 и
и 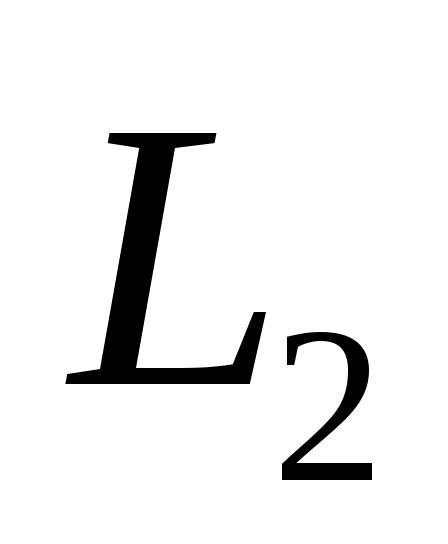 - регулярные языки, распознаваемые конечными автоматами
- регулярные языки, распознаваемые конечными автоматами 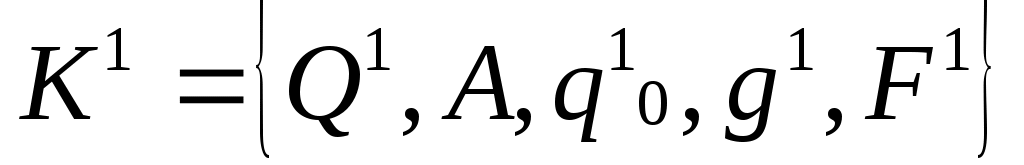 и
и  соответственно. Считаем, что
соответственно. Считаем, что 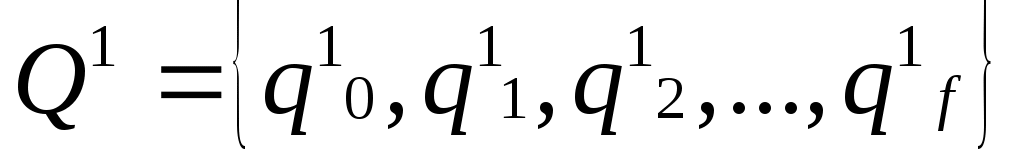 и
и 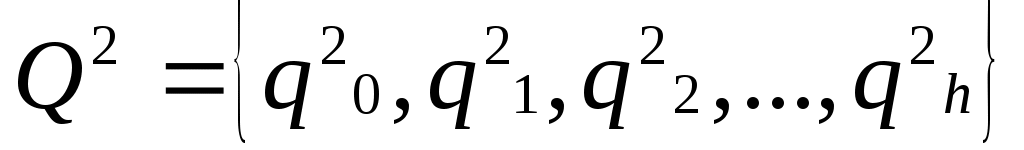 . Автомат
. Автомат 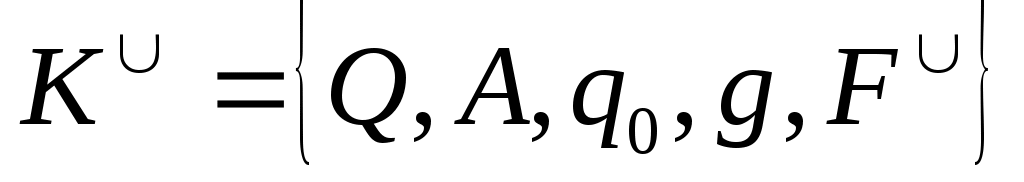 , распознающий язык
, распознающий язык 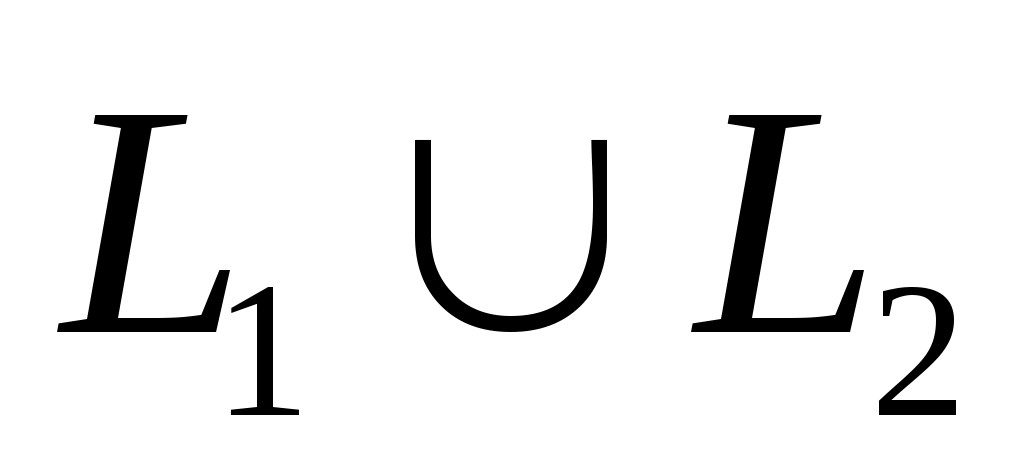 строим следующим образом. Полагаем
строим следующим образом. Полагаем 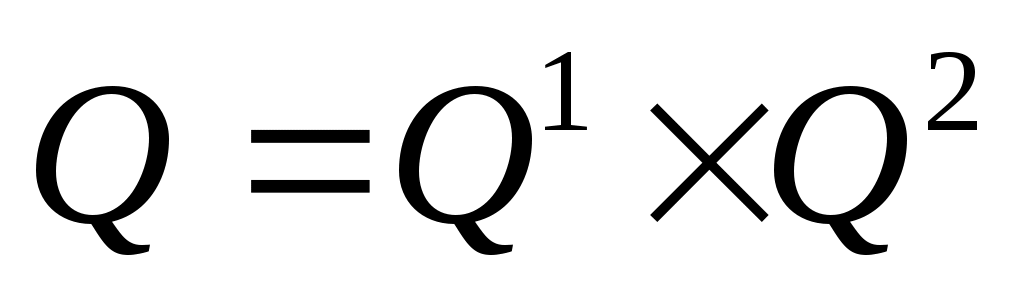 ; каждое состояние конструируемого автомата содержит две компоненты, левую и правую. Начальным состоянием нового автомата считаем
; каждое состояние конструируемого автомата содержит две компоненты, левую и правую. Начальным состоянием нового автомата считаем 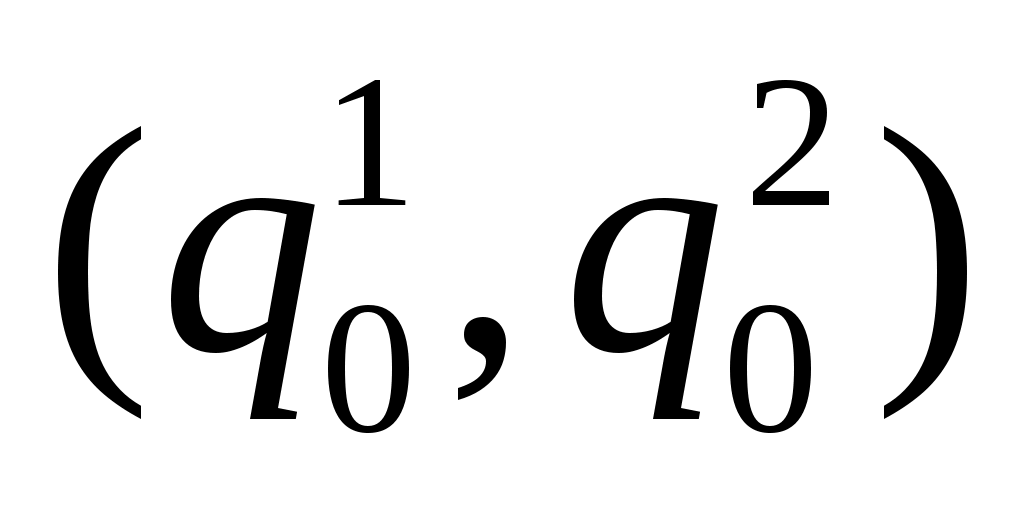 , а функцию переходов g определяем следующим образом:
, а функцию переходов g определяем следующим образом:
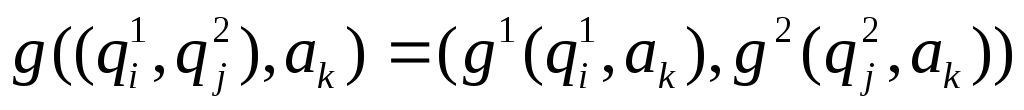 .
.
Очевидно, по первой компоненте автомат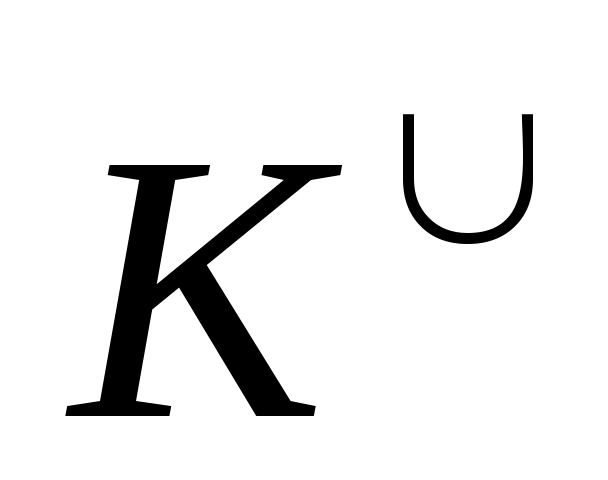 моделирует действия автомата
моделирует действия автомата 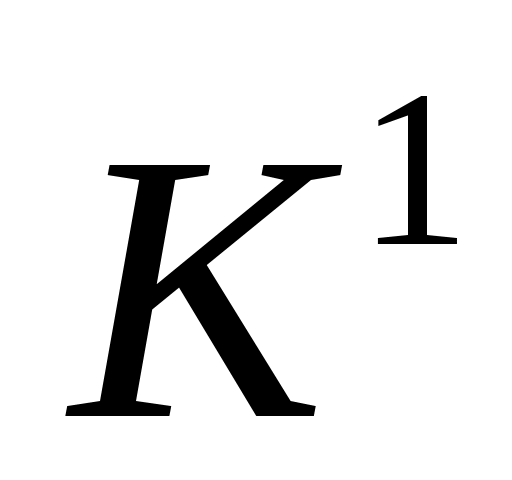
А и В содержат одинаковый сомножитель (подчеркнуты). Поэтому осуществляет операцию приведения подобных членов: в А или В заменяем его на 1 или, что то же самое, вычеркиваем его из А или из В.
Окончательно имеем с.к.н.ф.
F = АВ= (x1 x3 x2 x4) (x1 x3 x2 x4) (x1 x2 x4 x3).
Глава 4. РАСПОЗНАЮЩИЕ КОНЕЧНЫЕ АВТОМАТЫ
Распознающими конечными автоматами являются конечные автоматы, результатом работы которых является обнаружение некоторого свойства в заданном тексте. Обработку произвольного слова
Формально конечный автомат
где
);
Пусть
Слово
Определение 1. Язык
Конечный автомат удобно задавать диаграммой его переходов. Диаграмма представляет собой ориентированный граф, вершины которого одноименны состояниям автомата; дуга из вершины
На рис.1 примера 1 показана диаграмма автомата
из этого состояния не выходит; под воздействием буквы
П
 ример 1.
ример 1.Рисунок 1.
Класс регулярных языков замкнут относительно основных теоретико-множественных операций – объединения, пересечения, разности.
Пусть
Очевидно, по первой компоненте автомат