Файл: Методические указания к выполнению контрольной работы по дисциплине Дискретная математика для обучающихся 2 курса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 98
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
G соединяет единственная простая цепь;
5) G — ациклический граф, обладающий тем свойством, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
Задача об остове минимального веса(о кратчайшем остове): связном взвешенном графе (G, w) порядка n найти остов минимального веса.
Алгоритм Краскала, решающий эту задачу, заключается в следующем.
Алгоритм Прима отличается от алгоритма Краскала только тем, что на каждом этапе строится не просто ациклический граф, но дерево. Именно:
2. Если дерево Ti порядка i +1 уже построено и i<n— 1, то среди ребер, соединяющих вершины этого дерева с вершинами графа G, не входящими в Ti, выбираем ребро ei+1 минимального веса. Строим дерево Ti+1, присоединяя к Ti ребро ei+1 вместе с его не входящим в Тi концом.
Цикл в графе называется эйлеровым, если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом. Такой граф можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.
Помимо задачи о кёнигсбергских мостах известен ряд других старинных занимательных задач (головоломок), решение которых сводится к выяснению вопроса «являет
ся ли граф эйлеровым?». В одной из них требуется обрисовать фигуру, именуемую саблями (знаком) Магомета, не отрывая карандаша от бумаги и не повторяя линий.
Теорема. (Л. Эйлер, 1736 г.). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом. Задача определения содержит ли данный граф гамильтонов цикл является NP-полной.
Глава 3. МАТЕМАТИЧЕСКАЯ ЛОГИКА.
Логические операции над двумя высказываниями
Очевидно различных логических операций над двумя высказываниями имеется столько, сколько существует различных третьих столбцов в соответствующих таблицах истинности, а именно 24=16. Условимся обозначать эти операции символом fk и представим их следующей “сводной” таблицей истинности:
Совокупность из 16 операций fk можно разбить на 3 группы:
I. f0 0, f15 1.
II. f3 =
, f5 =
, f10 =
, f12 =
.
III. f1=
, f7=
,
f14=
, f8= 
,
f13=
, f2 =
,
f11 =
, f4 =
,
f9=
, f6= 
.
Формулы в АВ строятся по следующим правилам:
10. Переменная есть формула.
20.Если F и Ф - формулы, то и F , (FФ), (FФ), (FФ), (FФ) - тоже формулы.
30. Любая формула имеет вид, 10 или 20.
Например, выражение
является формулой.
Эквивалентные формулы.
1. Для конъюнкции и дизъюнкции:
, 
(1)
(закон противоречия), 
(закон исключенного третьего) (2)
,
(3)
, 
(4)
2. Для отрицания, конъюнкции и дизъюнкции:
(5)
(6)
(7)
Здесь (6) и (7) иногда называют законами де Моргана.
3. Законы дистрибутивности
(8)
(9)
Обозначив через x1 x2 любую из функций x1 x2 , x1 x2 . Тогда функция x1 x2 обладает свойством ассоциативности
(x1 x2 )x3 = x1 (x2 x3 ). (10)
4. Эквивалентные формулы
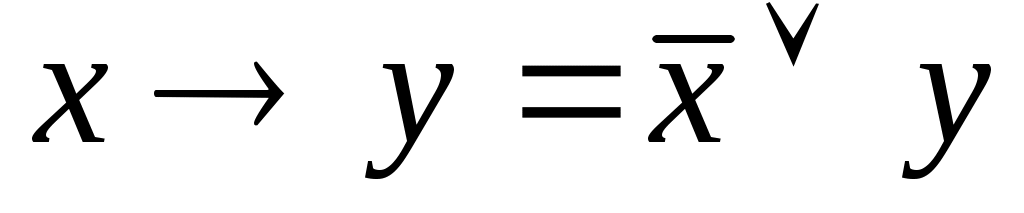(11)
(12)
(13)
Совершенные формы.
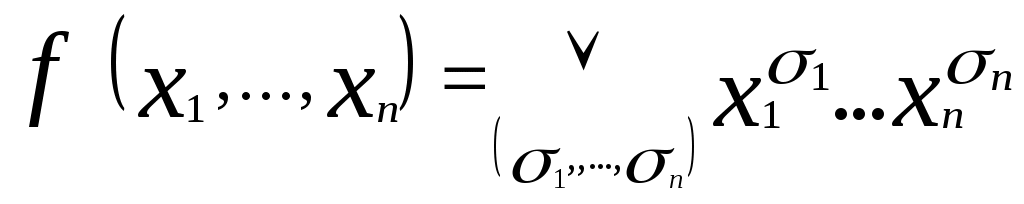(1)
Разложение вида (1) называется совершенной дизъюнктивной нормальной формой(с.д.н.ф.) и позволяет использовать следующий алгоритм построения с.д.н.ф. для всякой булевой функции f= f(x1, ..., xn), если f0.
Этап 1. В таблице, задающей f(x1, ..., xn), отмечаем все строки (1, ..., n), в которых
=1.
Этап 2. Для каждой отмеченной строки образуем конъюнкцию
(2)
Этап 3. Все полученные конъюнкции (1) соединим знаком дизъюнкции .
Преобразовать булеву формулу к с.д.н.ф. можно с помощью эквивалентных формул. Для этого избавляемся от импликации и эквиваленции и приводим формулу к д.н.ф. Далее дополняем недостающие переменные с помощью закона исключенного третьего.
(3)
Каждую булеву функцию f(x1,..., xn)1 можно представить в виде (3), где выражение (3) называется совершенной конъюнктивной нормальной формой (с.к.н.ф.)
Если булева функция задана таблицей истинности, то для построения с.к.н.ф. надо выбрать строки (1, ..., n), в которых
=0.
Для каждой отмеченной строки образуем дизъюнкцию
. Все полученные дизъюнкции соединим знаком конъюнкции.
Формулу F можно привести к с.к.н.ф. с помощью эквивалентных преобразований в два этапа.
Этап 1. Приведение F к виду к.н.ф. (F) с помощью законов (9.1)-(9.13).
Этап 2. Приведение к.н.ф. (F) к с.к.н.ф. [F]
Преобразование к.н.ф. (F) в с.к.н.ф. [F] осуществляется на базе закона дистрибутивности следующим образом:
Пусть к.н.ф.
содержит элементарную дизъюнкцию 
и пусть D не включает в себя переменную 
. Тогда осуществляем следующее тождественное преобразование:
.
Упражнение 1. Привести к с.к.н.ф. формулу
F=F(x1, x2, x3, x4) =(x1x3x2x3)( x1 x2 x4)
Этап 1. Приведем к к.н.ф.
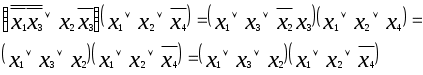(2)
Этап 2. Преобразование к.н.ф. в с.к.н.ф. с помощью законов дистрибутивности.
А= (x1 x3 x2 x4x4) = (x1 x3 x2 x4) (x1 x3 x2 x4)
В= x1 x2 x4 x3x3=(x1 x2 x4 x3) (x
5) G — ациклический граф, обладающий тем свойством, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
Задача об остове минимального веса(о кратчайшем остове): связном взвешенном графе (G, w) порядка n найти остов минимального веса.
Алгоритм Краскала, решающий эту задачу, заключается в следующем.
-
Строим граф t1 = Оn + е1, присоединяя к пустому графу на множестве вершин VG ребро е1 принадлежит EG минимального веса. -
Если граф Ti уже построен и i<n— 1, то строим граф Ti+1 — Ti + ei+1 , где ei+`1 — ребро графа G, имеющее минимальный вес среди ребер, не входящих в Ti и не составляющих циклов с ребрами из Тi.
Алгоритм Прима отличается от алгоритма Краскала только тем, что на каждом этапе строится не просто ациклический граф, но дерево. Именно:
-
Выбираем ребро е1 = аb минимального веса и строим дерево T1 полагая VT1 = {а, 6}, ЕТ1 = {е1}.
2. Если дерево Ti порядка i +1 уже построено и i<n— 1, то среди ребер, соединяющих вершины этого дерева с вершинами графа G, не входящими в Ti, выбираем ребро ei+1 минимального веса. Строим дерево Ti+1, присоединяя к Ti ребро ei+1 вместе с его не входящим в Тi концом.
Цикл в графе называется эйлеровым, если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом. Такой граф можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.
Помимо задачи о кёнигсбергских мостах известен ряд других старинных занимательных задач (головоломок), решение которых сводится к выяснению вопроса «являет
ся ли граф эйлеровым?». В одной из них требуется обрисовать фигуру, именуемую саблями (знаком) Магомета, не отрывая карандаша от бумаги и не повторяя линий.
Теорема. (Л. Эйлер, 1736 г.). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом. Задача определения содержит ли данный граф гамильтонов цикл является NP-полной.
Глава 3. МАТЕМАТИЧЕСКАЯ ЛОГИКА.
Логические операции над двумя высказываниями
Очевидно различных логических операций над двумя высказываниями имеется столько, сколько существует различных третьих столбцов в соответствующих таблицах истинности, а именно 24=16. Условимся обозначать эти операции символом fk и представим их следующей “сводной” таблицей истинности:
| x | y | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Совокупность из 16 операций fk можно разбить на 3 группы:
I. f0 0, f15 1.
II. f3 =
, f5 = , f10 = , f12 = .III. f1=
, f7= , f14=
, f8= , f13=
, f2 = , f11 =
, f4 = ,f9=
, f6= .Формулы в АВ строятся по следующим правилам:
10. Переменная есть формула.
20.Если F и Ф - формулы, то и F , (FФ), (FФ), (FФ), (FФ) - тоже формулы.
30. Любая формула имеет вид, 10 или 20.
Например, выражение
является формулой.Эквивалентные формулы.
1. Для конъюнкции и дизъюнкции:
, (1) (закон противоречия), (закон исключенного третьего) (2)
,
(3) , (4)2. Для отрицания, конъюнкции и дизъюнкции:
(5) (6) (7)Здесь (6) и (7) иногда называют законами де Моргана.
3. Законы дистрибутивности
(8) (9)Обозначив через x1 x2 любую из функций x1 x2 , x1 x2 . Тогда функция x1 x2 обладает свойством ассоциативности
(x1 x2 )x3 = x1 (x2 x3 ). (10)
4. Эквивалентные формулы
(11) (12) (13)Совершенные формы.
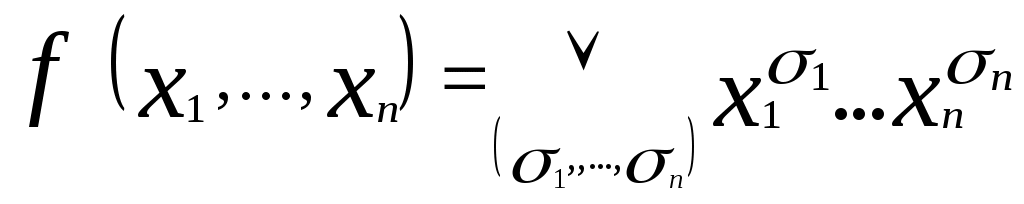(1)Разложение вида (1) называется совершенной дизъюнктивной нормальной формой(с.д.н.ф.) и позволяет использовать следующий алгоритм построения с.д.н.ф. для всякой булевой функции f= f(x1, ..., xn), если f0.
Этап 1. В таблице, задающей f(x1, ..., xn), отмечаем все строки (1, ..., n), в которых
=1.Этап 2. Для каждой отмеченной строки образуем конъюнкцию
(2)Этап 3. Все полученные конъюнкции (1) соединим знаком дизъюнкции .
Преобразовать булеву формулу к с.д.н.ф. можно с помощью эквивалентных формул. Для этого избавляемся от импликации и эквиваленции и приводим формулу к д.н.ф. Далее дополняем недостающие переменные с помощью закона исключенного третьего.
(3)Каждую булеву функцию f(x1,..., xn)1 можно представить в виде (3), где выражение (3) называется совершенной конъюнктивной нормальной формой (с.к.н.ф.)
Если булева функция задана таблицей истинности, то для построения с.к.н.ф. надо выбрать строки (1, ..., n), в которых
=0.Для каждой отмеченной строки образуем дизъюнкцию
. Все полученные дизъюнкции соединим знаком конъюнкции. Формулу F можно привести к с.к.н.ф. с помощью эквивалентных преобразований в два этапа.
Этап 1. Приведение F к виду к.н.ф. (F) с помощью законов (9.1)-(9.13).
Этап 2. Приведение к.н.ф. (F) к с.к.н.ф. [F]
Преобразование к.н.ф. (F) в с.к.н.ф. [F] осуществляется на базе закона дистрибутивности следующим образом:
Пусть к.н.ф.
содержит элементарную дизъюнкцию и пусть D не включает в себя переменную . Тогда осуществляем следующее тождественное преобразование: .Упражнение 1. Привести к с.к.н.ф. формулу
F=F(x1, x2, x3, x4) =(x1x3x2x3)( x1 x2 x4)
Этап 1. Приведем к к.н.ф.
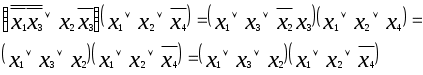(2)Этап 2. Преобразование к.н.ф. в с.к.н.ф. с помощью законов дистрибутивности.
А= (x1 x3 x2 x4x4) = (x1 x3 x2 x4) (x1 x3 x2 x4)
В= x1 x2 x4 x3x3=(x1 x2 x4 x3) (x