A(G)называется матрицей смежности графа G. Это симметрическая матрица с нулями на диагонали. Число единиц в строке равно степени соответствующей вершины.

Аналогично определяются матрицы смежности А мульти- и псевдографов: A_ijравно числу ребер, соединяющих вершины iи j (при этом петля означает два ребра).

Так же определяется матрица смежности A(G)ориентированного графа G:



Здесь AG— множество дуг орграфа G.

О
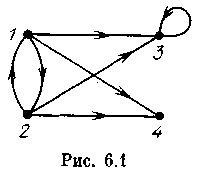
чевидно, что любая квадратная бинарная матрица является матрицей смежности некоторого ориентированного графа. На рис. 6.1 изображен ориентированный граф с матрицей смежности.

А
бстрактный граф приводит к различным матрицам смежности в зависимости от нумерации вершин.

Определим матрицу инцидентности графа. Пусть G-(n, m)-граф, VG = {1, 2, ..., n}, EG = {e₁, e₂, ..., e_m}. Определим бинарную nm-матрицу I = I(G)условиями:



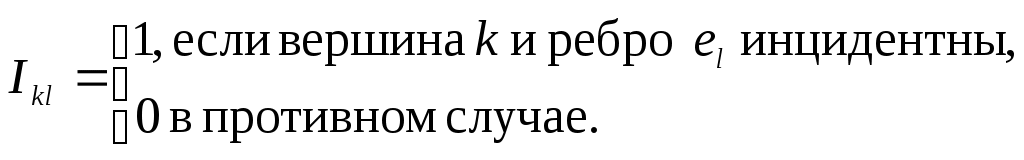
Матрица I называется матрицей инцидентности графа G. В каждом ее столбце ровно две единицы, равных столбцов нет. Как и выше, соответствие GI(G)является биекцией множества помеченных (n, m)-графов с занумерованными ребрами на множество nm-матриц, удовлетворяющих описанным условиям.

Для ориентированных графов определение матрицы

---

инцидентности I видоизменяется:



Метрические характеристики графа

Пусть G— связный граф, а uи v— две его несовпадающие вершины. Длина кратчайшего (u, v)-маршрута (он, естественно, является простой цепью) называется расстоянием между вершинами uи vи обозначается через d(u, v). Положим еще d(u, u)=0. Очевидно, что введенное таким образом расстояние удовлетворяет следующим аксиомам метрики:

1. 
   d(u, v)>= 0,
   
2. 
   d(u, v) = 0 тогда и только тогда, когда u = v,
   
3. 
   d(u, v)= d(v, и),
   
4. 
   d(u, v)+d(v, w) >= d(u, w)(неравенство треугольника).
   

Для фиксированной вершины uвеличина

н
азывается эксцентриситетом вершины u. Максимальный среди всех эксцентриситетов вершин называется диаметром графа Gи обозначается через d(G). Тем самым

В
ершина vназывается периферийной, если e(v)=d(

---

G). Простая цепь длины d(G), расстояние между концами которой равно d(G), называется диаметральной цепью.

Д
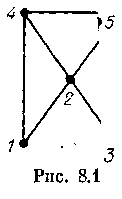
ля иллюстрации обратимся к графу на рис. 8.1. Здесь d(1, 2)=1, d(1, 3)=2; e(1)=2; d(G)=2. Все вершины, кроме вершины 2, являются периферийными, (1, 2, 3) — диаметральная цепь.

Минимальный из эксцентриситетов вершин связного графа называется его радиусом и обозначается через r(G):

О
чевидно, что радиус графа не больше его диаметра.

Вершина vназывается центральной, если e(v)= r(G). Множество всех центральных вершин графа называется его центром. Граф может иметь единственную центральную вершину или несколько центральных вершин. Наконец, центр графа может совпадать с множеством всех вершин.

Задача нахождения центральных вершин графа постоянно возникает в практической деятельности людей. Пусть, например, граф представляет сеть дорог, т. е. вершины его соответствуют отдельным населенным пунктам, а ребра — дорогам между ними. Требуется оптимально разместить больницы, магазины, пункты обслуживания. В подобных ситуациях критерий оптимальности часто заключается в оптимизации «наихудшего» случая, т. е. в минимизации расстояния от места обслуживания до наиболее удаленного пункта. Следовательно, местами размещения должны быть центральные вершины графа.

Инварианты графа

Условимся использовать обозначения

- изоморфизм графовG и G’;

М – множество, элементами которого могут быть числа

---

, векторы, многочлены, матрицы, системы чисел;

F – функция, которая каждому графу G ставит в соответствие некоторый элемент f(G) из множества М.

Функцию f называют инвариантом, если на изоморфных графах ее значения совпадают, т.е. для любых графов G и G’ выполняется соотношение ↔

f(G) = f(G’).

Кликой называют всякий наибольший полный подграф данного графа, размер клики – число вершин в ней.

Определим наиболее важные инварианты графа.
1⁰. Вектор степеней графа - это упорядоченный (по возрастанию или убыванию) перечень степеней вершин .

2⁰. Число внешней устойчивости или плотности - это число вершин максимальной клики в графе G. Другими словами, - это наибольшее количество попарно смежных вершин в G.

Иногда плотность называют кликовым числом.

Наименьшее число клик графа G, покрывающих множество V, называется числом кликового покрытия и обозначается через с(G).

3⁰. Число внутренней устойчивости или неплотность графа - это наибольшее количество его попарно несмежных вершин. Приведем другое определение. Подмножество называется независимым (или внутренне устойчивым), если в нем любая пара вершин не смежна. Т.е. если независимо в G , то порожденный подграф состоит только из изолированных вершин.

---

Независимое множество называется максимальным, если оно не является собственным подмножеством другого независимого множества.

Наибольшее по мощности независимое множество в графе G называется наибольшим, а его мощность равна .

Примечание. Для всякого полного графа значение =1, а число внешней устойчивости = .

Задачи определения точного значения очень трудны.

4⁰. Хроматическое число.

Рассмотрим правильные k-раскраски графа G. Минимальное число k, при котором граф G является k-раскрашиваемым, называется хроматическим числом этого графа и обозначается . Правильная k-раскраска графа G при называется минимальной.

Если для графа G , то G называется бихроматическим.

5⁰. Число компонент связности K(G).

6⁰. Числом Хадвигера связного графа G называется количество вершин наибольшей клики, на которую можно стянуть данный граф.

Деревья

Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами леса являются деревья. На рис. 13.1 изображены все деревья шестого порядка.

Существует несколько вариантов определения дерева; некоторые из них отражены в следующей теореме.

Теорема. Для (n, m)-графа G следующие ут­верждения эквивалентны .

1. 
   G — дерево;
   
2. 
   G — связный граф и m = n — 1;
   

3) G — ациклический граф и m = n — 1;

4) любые две несовпадающие вершины графа

---

Смотрите также файлы

• По учебному курсу Управление бизнеспроцессами.docx

• 90к3ушоацсвш9щ0льацувысш0щлзпкьавм 90к3ушоацсвш9щ0льацувысш0щлзпкьавм 90к3ушоацсвш9щ0льацувысш0щлзпкьавм.docx

• Что такое Земский собор, каким был его состав.docx

• Закона 323 от 21. 11. 2011 Об основах охраны здоровья граждан в Российской Федерации.docx

• Несмотря на разногласия источников, считается, что Рим был захвачен этрусской армией примерно в 509 году до н э. в рамках свержения Тарквиния Гордого.pptx