Методические указания по выполнению контрольной работы

по дисциплине «Дискретная математика»

Глава 1. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
В комбинаторном анализе рассматриваются задачи о расположениях элементов в соответствии с точно определенными требованиями, и выясняется, сколькими различными вариантами такие расположения могут быть осуществлены. При этом необходимо однозначно определить, какие решения считаются различными.

Одними из основных средств, для подсчета числа решений комбинаторных задач являются выборки, к которым относятся размещения, сочетания и перестановки.

Рассмотрим множество , .

Определение 1. Набор элементов из называется выборкой объема k из n элементов или (n, k) – выборкой.

Выборки могут отличаться друг от друга, как составом, так и порядком расположения элементов. Если допустить, что среди элементов выборки есть одинаковые, то объем выборки в отдельных случаях может превышать объем исходного множества.

Выборка называется упорядоченной, если порядок элементов в ней задан. То есть, упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.

Если порядок следования элементов не является существенным, то выборка называется неупорядоченной.

В выборке могут допускаться или не допускаться повторения элементов. Таким образом, можно говорить о (n, k) – выборках без повторений и о (n, k) – выборках с повторениями.

Положим n=3, k=2 и рассмотрим множество , представим для него все случаи (3,2)-выборок.

1. 
   неупорядоченные без повторения (1,2) ; (1,3); (2,3);
   
2. 
   неупорядоченные с повторениями (1,1); (1,2); (2,2); (1,3); (3,3); (2,3);
   
3. 
   упорядоченные без повторений (1,2); (2,1); (1,3); (3,1); (2,3); (3,2);
   
4. 
   упорядоченные с повторениями (1,2); (2,1); (1,3); (3,1); (2,3); (3,2); (1,1); (2,2); (3,3);
   

Определение 2. Упорядоченная (

---

n, k) – выборка без повторений называется размещением из n элементов по k или кратко (n, k) – размещением.

Определение 3. Упорядоченная (n, k) – выборка с повторениями называется размещением с повторениями из n элементов по k или кратко (n, k) – размещением с повторениями.

Определение 4. Неупорядоченная (n, k) – выборка без повторений называется сочетанием из n элементов по k или кратко (n, k) – сочетанием.

Определение 5. Неупорядоченная (n, k) – выборка с повторениями называется сочетанием с повторениями из n элементов по k или кратко (n, k) – сочетанием с повторениями.

Определение 6. Если n=k, то (n, n) – размещение называется перестановкой n элементов.

Число всех (n, k) – размещений обозначается символом или и вычисляется по формуле .

Действительно, размещение k элементов можно представить как заполнение некоторых k позиций элементами множества . При этом первую позицию можно заполнить n различными способами. После того как 1-я позиция заполнена, элемент для заполнения 2-й позиции можно выбрать (n-1) способами. Если продолжить этот процесс, то после заполнения позиций с 1-й по (k -1)-ю будем иметь (n-k+1) способов заполнения последней, k-й позиции. Перемножая эти числа, получим формулу .

Число всех (n, k) – размещений с повторениями обозначается символом или и вычисляется по формуле

---

.

Действительно, размещение k элементов можно представить как заполнение некоторых k позиций элементами множества . При этом первую позицию можно заполнить n различными способами. После того как 1-я позиция заполнена, элемент для заполнения 2-й позиции можно выбрать тоже n способами. Если продолжить этот процесс, то для заполнения последней, k-й позиции будем иметь тоже n способов. Перемножая эти числа, получим формулу .

Число всех перестановок n элементов обозначается символом или и вычисляется по формуле .

Действительно, .

Число всех (n, k) – сочетаний обозначается символом или и вычисляется по формуле .

В каждом из сочетаний имеется k различных элементов, поэтому на базе каждого сочетания можно получить перестановок. Совокупность всех выборок, полученных путем построения всех перестановок на базе каждого из сочетаний, представляет собой число размещений , т.е. откуда .

Число всех (n, k) – сочетаний с повторениями обозначается символом

---

или и вычисляется по формуле .
Задачи на применение формул подсчета числа различных выборок.
1. Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9, если все цифры в каждом четырехзначном числе различны?

, n=9, k=4. .

2. На тренировках занимаются 12 баскетболистов. Сколько может быть образовано тренером разных стартовых пятерок?

, n=12, k=5. .

3. Сколько различных наборов по 8 пирожных в каждом можно составить используя 4 сорта пирожных?

, n=4, k=8. .

4. Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать если использовать 5 символов?

, n=2, k=5. /

5. Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг?

n=7.

При подсчете числа различных комбинаций используются следующие два правила:

1. 
   Правило произведения. Если объект может быть выбран способами и после каждого из таких выборов объект 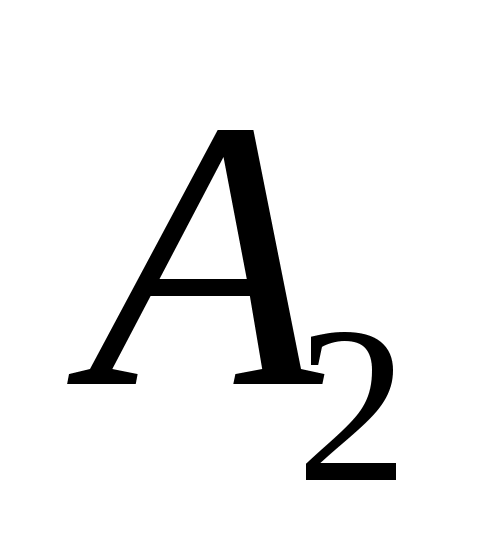в свою очередь может быть выбран способами, то выбор « и 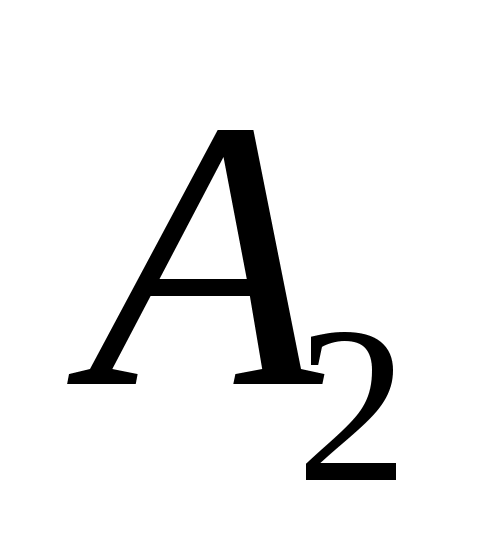» в указанном порядке может быть осуществлен ∙ способами.
   
2. 
   Правило суммы. Если объект может быть выбран способами, а объект 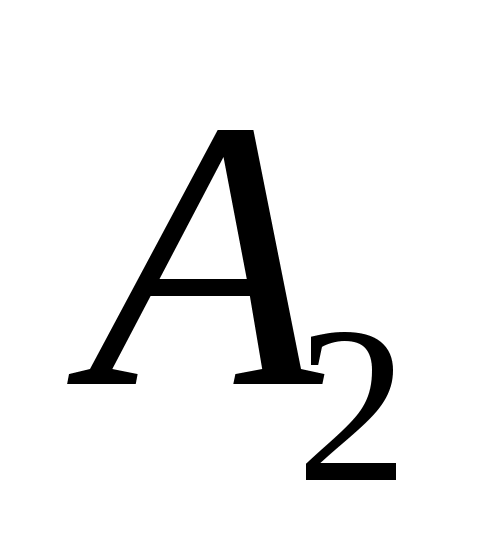может быть выбран другими способами, то выбор « или 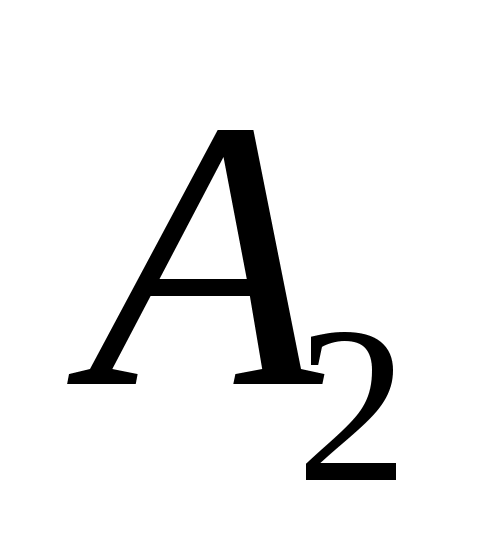» может быть осуществлен + способами.
   

---

Задачи на правило произведения и правило суммы.

1. 
   Правило произведения.
   

Для полета на Марс необходимо укомплектовать следующий экипаж космического корабля: командир, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся к полету летчиков, два бортинженера – из числа 20 специалистов, врач – из числа 8 медиков. Сколькими способами можно укомплектовать экипаж?

Решение: командующая тройка - т.к. важен порядок, у бортинженеров обязанности одинаковые - , врач - . Весь экипаж - и и , что соответствует способами.

2. 
   Правило суммы.
   

Сколько существует различных телефонных номеров, если считать, что каждый номер содержит не более семи цифр (телефонный номер может начинаться с 0)?

Решение: .

Воспользовались формулой суммы геометрической прогрессии при q>1: .

Перестановки с повторениями.

Пусть имеются предметы k различных видов. Сколько существует перестановок из элементов первого типа, элементов второго типа,…, из элементов k­­-того типа.

Пусть дано множество M: M={a,a,a,b,b,c,d,d,d,d}, n=10, a повторяется 3 раза, b повторяется 2 раза, c повторяется 1 раз и d повторяется 4 раза.

Рассмотрим перестановки элементов этого множества, если все элементы различны:

---

Смотрите также файлы

• По учебному курсу Управление бизнеспроцессами.docx

• 90к3ушоацсвш9щ0льацувысш0щлзпкьавм 90к3ушоацсвш9щ0льацувысш0щлзпкьавм 90к3ушоацсвш9щ0льацувысш0щлзпкьавм.docx

• Что такое Земский собор, каким был его состав.docx

• Закона 323 от 21. 11. 2011 Об основах охраны здоровья граждан в Российской Федерации.docx

• Несмотря на разногласия источников, считается, что Рим был захвачен этрусской армией примерно в 509 году до н э. в рамках свержения Тарквиния Гордого.pptx