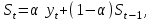
где 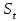- значение экспоненциальной средней в момент t;

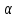- параметр сглаживания, .

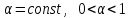В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше 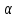, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий быстро убывает. При малом 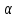прогнозные оценки учитывают все наблюдения, при этом уменьшение влияние более «старой» информации происходит медленно.

Для определения параметра сглаживания существуют различные методы: метод Брауна и метод Мейера, метод подбора минимизирующего ошибку прогноза, рассчитанного на ретроспективных данных.

Также наиболее широко применяемыми и зарекомендовавшими себя являются две разновидности метода экспоненциального сглаживания: двухпараметрический метод Хольта и метод Винтерса. Двухпараметрический метод Хольта позволяет учесть изменение тренда. Метод Винтерса является модификацией двухпараметрического метода Хольта, который позволяет учесть помимо изменения тренда фактор сезонности.

Применение методов экстраполяции в достаточной мере ограничено самим объектом прогнозирования. Если речь идет о прогнозировании социально-экономического развития региона, то логичнее представлять его в виде сложной и открытой системы. Анализ ретроспективной информации позволяет выявить особенности и причины, которые привели систему в текущее состояние. Однако прогнозы, построенные только на базе ретроспективной информации относительно объекта прогнозирования, далеко не всегда совпадают с реальностью. Методы экстраполяции хорошо подходят в периоды инерционного развития, когда тенденции прошлого развития объекта сохраняются, а воздействие внешних факторов остается неизменными. Фактически методы экстраполяции не способны напрямую учитывать изменение воздействия внешних факторов. Учитывая требование законодательства, о необходимости построения нескольких вариантов прогнозов, данные методы прогнозирования могут рассматриваться в качестве инструментов для прогнозирования отдельных процессов и явлений.

---

МЕТОДЫ МОДЕЛИРОВАНИЯ

Наиболее адекватными для прогнозирования любых социально-экономических процессов являются методы моделирования. В рамках данной группы можно выделить следующие наиболее значимые методы прогнозирования: модели оптимального прогнозирования, эконометрические модели (факторные модели), имитационные модели.

Наиболее известным методом прогнозирования экономических процессов при помощи матричных моделей является метод межотраслевого баланса.

Метод межотраслевого баланса был особо актуален в советский период. В условиях фиксации на будущее объемов производства и конечного потребления, задача заключалась в поиске прогнозной матрицы коэффициентов прямых затрат, каждый элемент которой минимально отличается от соответствующего элемента последнего отчетного баланса. В современных условиях развития экономики крайне сложно применять данный метод для прогнозирования социально-экономического развития регионов. В настоящий момент времени не существует нормативов потребления продукции, производителям не установлены нормы производства продукции, всё это часто приводит к неоптимальному использованию ресурсов в рамках страны. Также согласно действующему законодательству государство не может регулировать объемы производства и потребления продукции в частном секторе экономики (за исключением отдельных случаев). Следствием этого является практическая невозможность и нецелесообразность применения данного метода для прогнозирования социально-экономического развития регионов.

Модели оптимального прогнозирования призваны определить оптимальные варианты развития экономики. Данные методы прогнозирования позволяют выбрать наилучший из потенциально возможных вариантов развития того или иного процесса или всей экономики в целом. Суть метода заключается в задании ряда ограничений (в качестве ограничений, как правило, выступают ограничения по времени и по ресурсам), а также в определении целевой функции, которая описывает цель оптимизации. Сущность метода сводится к поиску экстремума целевой функции на прогнозном интервале, при условии соблюдении всех ограничений. В качестве целевой функции на макроуровне может выступать функция описывающая объем валового внутреннего продукта, валового регионального продукта, доходов населения и т.п.

К настоящему времени разработаны многие принципы и методологические основы целевого подхода к задачам управления и прогнозирования экономических систем. Их изложение дано в работах А.И. Анчишкина, Д.Л. Андрианова, А.Г. Гранберга, Е.З. Майминаса, А.Е. Илютовича,

---

Ю.Н. Черемных и других исследователей.

Несмотря на большое количество разработанных моделей оптимального прогнозирования, а также достаточное количество программных продуктов, позволяющих с минимальными трудозатратами строить соответствующие прогнозы, данные методы прогнозирования не часто используются на региональном уровне. В первую очередь это связано с тем, что для построения подобных моделей требуется высокая квалификация прогнозиста.

В рамках эконометрических моделей выделяют две основные подгруппы: однофакторные и многофакторные модели. Подобно методам экстраполяции данные методы достаточно эффективны в периоды стабильного развития экономических систем. В тоже время при использовании данных методов совместно с методами экспертных оценок можно строить адекватные прогнозы и для случаев существенного изменения внешней среды.

Однофакторные модели прогнозирования представляют собой построение прогноза с помощью уравнения одной переменной 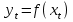. Однофакторные модели могут быть описаны различными типами уравнений: линейными, экспоненциальными, параболическими, гиперболическими, степенными, логарифмическими и др.

Сущность данного метода прогнозирования заключается в том, что при известном значении фактора (от которого зависит прогнозная величина) на прогнозном интервале, при помощи зависимости, построенной на основе данных на историческом интервале (ретроспективных данных), можно получить прогноз. В самом простом случае, когда в роли независимого фактора выступает время, то однофакторные экономико-статистические модели представляют собой модели экстраполяции.

В случае, когда строится зависимость не от одного фактора, а от нескольких, подобные модели называются многофакторными 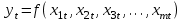. Подобно однофакторным моделям многофакторные модели могут описываться различными типами функций. Подобные уравнения однофакторной и многофакторной моделей носят названия регрессионных уравнений. Например, степенная многофакторная модель имеет вид:

,

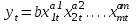где 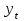– значение прогнозируемой величины в момент времени t;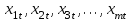

---

– значение независимых факторов в момент времени t;

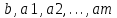– коэффициенты или параметры регрессионного уравнения.

Прогнозирование в случае применения многофакторной модели осуществляется аналогично случаю однофакторной модели. На первом этапе на основе ретроспективной информации по объекту прогнозирования и независимым факторам определяется вид зависимости между ними. На следующем этапе строятся прогнозы независимых факторов (при этом могут использоваться различные методы, в том числе и методы экспертных оценок). Затем на основе прогнозов независимых факторов и построенной зависимости строится прогноз для объекта прогнозирования.

При исследовании экономических процессов нередко приходится моделировать ситуации, когда значение зависимой переменной в текущий момент времени 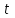формируется под воздействием ряда факторов, действовавших в прошлые моменты времени 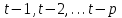. Величину 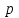, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, - лаговыми переменными. Модели, содержащие не только текущие, но и лаговые значения факторных переменных называются моделями с распределенным лагом. Модель вида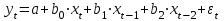



является примером модели с распределенным лагом.

Наряду с лаговыми значениями независимых переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Такое влияние обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида



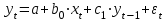
относится к моделям авторегрессии.

Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику.Во-первых, оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК

---

, ввиду нарушения его предпосылок и требует специальных статистических методов.Во-вторых, исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры. Наконец, в-третьих, между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.

Также одной из разновидностей методов эконометрического моделирования является использование системы эконометрических уравнений. Построение изолированных уравнений регрессии недостаточно для описания региональной системы. При использовании отдельных уравнений регрессии, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. В тоже время многие макроэкономические показатели взаимосвязаны и взаимодействуют между собой, т.е. изменение одного показателя, как правило, не может происходить при абсолютной неизменности других.

Система уравнений содержит эндогенные и экзогенные переменные. Эндогенные или объясняемые переменные – это зависимые переменные, число которых равно числу уравнений в системе. Экзогенные или объясняющие переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

Система уравнений в эконометрических исследованиях может быть построена по-разному:

1) Система независимых уравнений. В данной системе каждая зависимая переменная 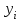рассматривается как функция одного и того же набора факторов :



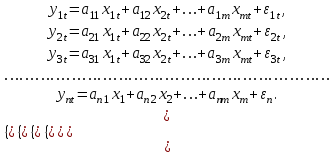
Набор факторов 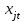в каждом уравнении может варьироваться. Отсутствие того или иного фактора в уравнении системы может быть следствием как экономической нецелесообразности его включения в модель, так и несущественности его воздействия на результативный признак.

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно и по существу является уравнением регрессии. Для нахождения его параметров можно использовать метод наименьших квадратов.

2) Система рекурсивных уравнений. В данной системе зависимая переменная включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов

---

Смотрите также файлы

• Влияние физической культуры и спорта на организм человека.rtf

• 1 хаттамасы маусым 2023ж саат минуттан саат минута дейін Абдрашид Ділшат лы 1304000Есептеу техникасы жне бадарламамен амтасыз ету.docx

• Организационная структура и взаимодействие подразделений организации с бухгалтерией (кассой).docx

• Организационное обеспечение (ОО).docx

• Теоретические основы организации рекламной деятельности в туристическом бизнесе.docx