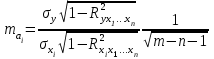Файл: Обоснование метода математического прогнозирования несчастных случаев и профессиональных заболеваний.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 270
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 + 61259,9a2 + 2635,1a3
11015 = 313,6a0 + 7966,2a1 + 1650687,6a2 + 70811,3a3
239420,9= 61259,9a0 + 1650687,6a1 +398462769,9 a2 + 15804692,9 a3
98476,2= 2635,1a0 +70811,3 a1 +15804692,9 a2 +674761,3 a3
Значения неизвестных параметров системы находятся методом Крамера.
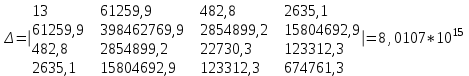
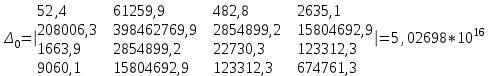
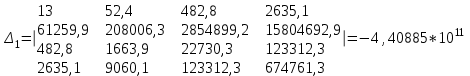
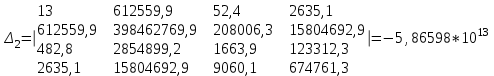
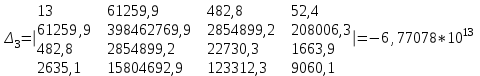
Искомые значения коэффициентов уравнения находятся по формуле:
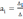
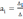 (13)
(13)
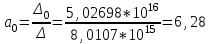
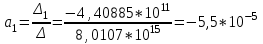
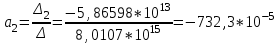
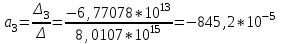
По найденным параметрам составляется уравнение регрессии:
Кч = 6,28 – 5,5*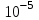 S - 732,3*
S - 732,3*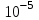 I –845,2*
I –845,2*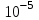 V
V
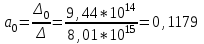
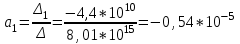
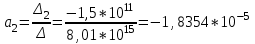
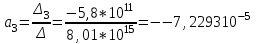
Уравнение регрессии:
Кл = 0,1179 – 0,54*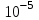 S – 1,8*
S – 1,8*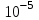
I – 7,2* V
V
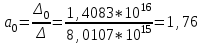
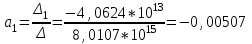
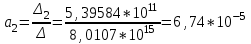
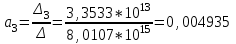
Уравнение регрессии:
Кп.з. = 1,76 – 507* V + 6,74*
V + 6,74* S + 493,5*
S + 493,5* I
I
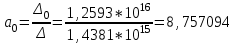
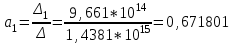
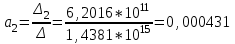
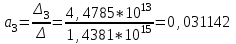
Уравнение регрессии:
Кт = 8,757 + 0,6718d + 0,000431S + 0,03114V
Коэффициент множественной корреляции
Если частные коэффициенты корреляции модели множественной регрессии оказались значимыми, т. е. между результативной переменной и факторными модельными переменными действительно существует корреляционная взаимосвязь, то в этом случае построение множественного коэффициента корреляции считается целесообразным.
С помощью множественного коэффициента корреляции характеризуется совокупное влияние всех факторных переменных на результативную переменную в модели множественной регрессии.
Формула для определения коэффициента корреляции уравнения множественной регрессии через матрицу парных коэффициентов корреляции:
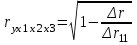 . (14)
. (14)
где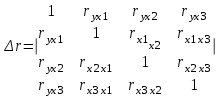 - определитель матрицы парных коэффициентов корреляции;
- определитель матрицы парных коэффициентов корреляции;
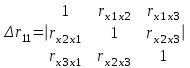 - определитель матрицы межфакторной корреляции.
- определитель матрицы межфакторной корреляции.
Как видно из формул
, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
Таблица 14 – Результаты расчетов множественного коэффициента корреляции
Оценка качества построенной модели
Коэффициентом множественной детерминации R2 называется квадрат множественного коэффициента корреляции.
Коэффициент множественной детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
Для коэффициента множественной детерминации всегда выполняется неравенство вида:
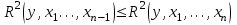 . (15)
. (15)
Следовательно, включение в линейную модель регрессии дополнительной факторной переменной не снижает значения коэффициента множественной детерминации.
Таблица 15 – Рассчитанные коэффициенты детерминации
Для того чтобы не допустить преувеличения тесноты связи, применяется скорректированный индекс множественной детерминации, который содержит поправку на число степеней свободы и рассчитывается по формуле:
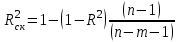 . (16)
. (16)
где n – объем выборки, m – число переменных в уравнении множественной регрессии. При небольшом числе наблюдений нескорректированная величина коэффициента множественной детерминации R2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.
Таблица 16 - Скорректированный индекс множественной детерминации
Высокие величины коэффициентов детерминации R2 указывают на то, что модели регрессии хорошо аппроксимируют исходные данные и такими регрессионными моделями можно воспользоваться для прогноза значений результативного показателя.
Проверить значимость (качество) уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным, достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. Чтобы иметь общее суждение о качестве модели, по каждому наблюдению из относительных отклонений определяют среднюю ошибку аппроксимации. Проверка адекватности уравнения регрессии (модели) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 12-15% (максимально допустимое значение).
Формула для расчета средней ошибки аппроксимации:
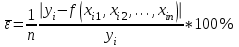 , (17)
, (17)
где n – число переменных в уравнении множественной регрессии; f(xi1, xi2, …, xin) – i-е расчетное значение переменной y; - i-е опытное значение переменной y.
- i-е опытное значение переменной y.
Таблица 17 - Средняя ошибка аппроксимации
Как видно из результата расчетов, средние ошибки аппроксимации не превышают допустимые значения в 12-15%, что говорит об адекватности полученных моделей.
Проверка значимости коэффициентов линейного уравнения множественной регрессии.
Проверка значимости отдельных коэффициентов уравнения означает, что если коэффициент при некоторой переменной незначим, то доверять влиянию этой переменной на значения результирующей функции y нельзя. Незначимый коэффициент следует положить равным нулю, т.е. соответствующую переменную следует исключить из дальнейшего рассмотрения.
Для проверки значимости каждого из коэффициентов a0, a1,…, an используется t-статистика Стьюдента, опытное значение которой вычисляется по формуле:
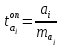 , (i=0,1,…,n), (18)
, (i=0,1,…,n), (18)
где ai – коэффициент при переменной xi,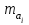 - среднеквадратическая ошибка этого коэффициента,
- среднеквадратическая ошибка этого коэффициента,
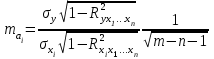
11015 = 313,6a0 + 7966,2a1 + 1650687,6a2 + 70811,3a3
239420,9= 61259,9a0 + 1650687,6a1 +398462769,9 a2 + 15804692,9 a3
98476,2= 2635,1a0 +70811,3 a1 +15804692,9 a2 +674761,3 a3
Значения неизвестных параметров системы находятся методом Крамера.
-
Решение системы уравнений для коэффициента частоты травматизма (Кч):
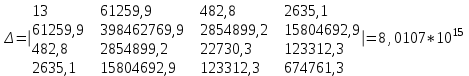
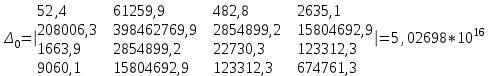
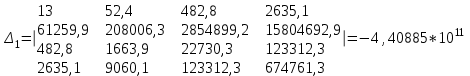
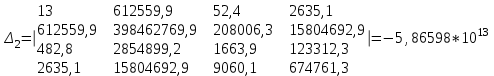
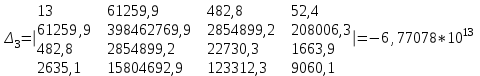
Искомые значения коэффициентов уравнения находятся по формуле:
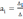
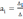 (13)
(13)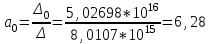
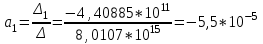
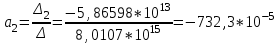
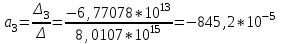
По найденным параметрам составляется уравнение регрессии:
Кч = 6,28 – 5,5*
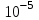 S - 732,3*
S - 732,3*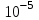 I –845,2*
I –845,2*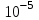 V
V-
Решение системы уравнений для коэффициента частоты смертельных исходов Кс.и.:
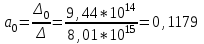
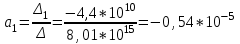
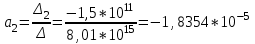
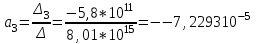
Уравнение регрессии:
Кл = 0,1179 – 0,54*
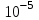 S – 1,8*
S – 1,8*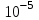
I – 7,2*
 V
V-
Решение системы уравнений для коэффициента частоты профессиональных заболеваний Кп.з.:
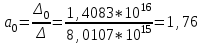
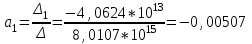
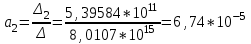
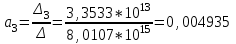
Уравнение регрессии:
Кп.з. = 1,76 – 507*
 V + 6,74*
V + 6,74* S + 493,5*
S + 493,5* I
I-
Решение системы уравнений для коэффициента тяжести Кт:
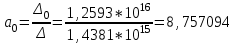
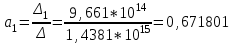
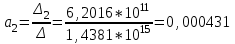
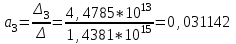
Уравнение регрессии:
Кт = 8,757 + 0,6718d + 0,000431S + 0,03114V
Коэффициент множественной корреляции
Если частные коэффициенты корреляции модели множественной регрессии оказались значимыми, т. е. между результативной переменной и факторными модельными переменными действительно существует корреляционная взаимосвязь, то в этом случае построение множественного коэффициента корреляции считается целесообразным.
С помощью множественного коэффициента корреляции характеризуется совокупное влияние всех факторных переменных на результативную переменную в модели множественной регрессии.
Формула для определения коэффициента корреляции уравнения множественной регрессии через матрицу парных коэффициентов корреляции:
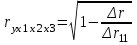 . (14)
. (14)где
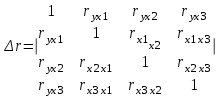 - определитель матрицы парных коэффициентов корреляции;
- определитель матрицы парных коэффициентов корреляции;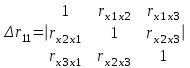 - определитель матрицы межфакторной корреляции.
- определитель матрицы межфакторной корреляции.Как видно из формул
, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
Таблица 14 – Результаты расчетов множественного коэффициента корреляции
| Показатель травмирования | 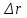 | 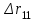 | r |
| Кч | 0,0005 | 0,0084 | 0,967 |
| Кл | 0,0026 | 0,0084 | 0,830 |
| Кп.з. | 0,0011 | 0,0084 | 0,935 |
| Кт | 0,0021 | 0,0177 | 0,939 |
Оценка качества построенной модели
Коэффициентом множественной детерминации R2 называется квадрат множественного коэффициента корреляции.
Коэффициент множественной детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии. Чем больше значение коэффициента множественной детерминации, тем лучше построенная модель регрессии характеризует взаимосвязь между переменными.
Для коэффициента множественной детерминации всегда выполняется неравенство вида:
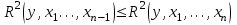 . (15)
. (15)Следовательно, включение в линейную модель регрессии дополнительной факторной переменной не снижает значения коэффициента множественной детерминации.
Таблица 15 – Рассчитанные коэффициенты детерминации
| Показатель травмирования | Кч | Кл | Кп.з. | Кт |
| R2 | 0,935 | 0,690 | 0,874 | 0,881 |
Для того чтобы не допустить преувеличения тесноты связи, применяется скорректированный индекс множественной детерминации, который содержит поправку на число степеней свободы и рассчитывается по формуле:
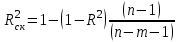 . (16)
. (16)где n – объем выборки, m – число переменных в уравнении множественной регрессии. При небольшом числе наблюдений нескорректированная величина коэффициента множественной детерминации R2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.
Таблица 16 - Скорректированный индекс множественной детерминации
| Показатель травмирования | Кч | Кл | Кп.з. | Кт |
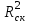 | 0,913 | 0,587 | 0,832 | 0,842 |
Высокие величины коэффициентов детерминации R2 указывают на то, что модели регрессии хорошо аппроксимируют исходные данные и такими регрессионными моделями можно воспользоваться для прогноза значений результативного показателя.
Проверить значимость (качество) уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным, достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. Чтобы иметь общее суждение о качестве модели, по каждому наблюдению из относительных отклонений определяют среднюю ошибку аппроксимации. Проверка адекватности уравнения регрессии (модели) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 12-15% (максимально допустимое значение).
Формула для расчета средней ошибки аппроксимации:
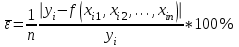 , (17)
, (17)где n – число переменных в уравнении множественной регрессии; f(xi1, xi2, …, xin) – i-е расчетное значение переменной y;
 - i-е опытное значение переменной y.
- i-е опытное значение переменной y.Таблица 17 - Средняя ошибка аппроксимации
| Показатель травмирования | Кч | Кл | Кп.з. | Кт |
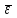 , % , % | 6,3 | 10,5 | 6,5 | 5,6 |
Как видно из результата расчетов, средние ошибки аппроксимации не превышают допустимые значения в 12-15%, что говорит об адекватности полученных моделей.
Проверка значимости коэффициентов линейного уравнения множественной регрессии.
Проверка значимости отдельных коэффициентов уравнения означает, что если коэффициент при некоторой переменной незначим, то доверять влиянию этой переменной на значения результирующей функции y нельзя. Незначимый коэффициент следует положить равным нулю, т.е. соответствующую переменную следует исключить из дальнейшего рассмотрения.
Для проверки значимости каждого из коэффициентов a0, a1,…, an используется t-статистика Стьюдента, опытное значение которой вычисляется по формуле:
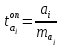 , (i=0,1,…,n), (18)
, (i=0,1,…,n), (18)где ai – коэффициент при переменной xi,
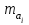 - среднеквадратическая ошибка этого коэффициента,
- среднеквадратическая ошибка этого коэффициента,