Файл: Обоснование метода математического прогнозирования несчастных случаев и профессиональных заболеваний.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 267
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, (19)
где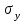 - среднее квадратичное отклонение для значений переменной y;
- среднее квадратичное отклонение для значений переменной y; 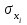 - среднее квадратичное отклонение для значений xi;
- среднее квадратичное отклонение для значений xi; 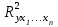 - коэффициент множественной детерминации для уравнения регрессии в целом;
- коэффициент множественной детерминации для уравнения регрессии в целом; 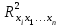 - коэффициент множественной детерминации, характеризующий зависимость между фактором xi и остальными факторами (x1, x2,…, xi-1, xi+1,…, xn)уравнения регрессии.
- коэффициент множественной детерминации, характеризующий зависимость между фактором xi и остальными факторами (x1, x2,…, xi-1, xi+1,…, xn)уравнения регрессии.
Каждое из опытных значений статистики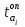 сравнивают с критическим значением
сравнивают с критическим значением 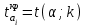 (i=1,2,…,n), которое ищется по таблице распределения Стьюдента при заданном уровне значимости α и числе степеней свободы k, равном k=m-n-1. В данном случае при уровне значимости α=0,05 и k=13-3-1=9
(i=1,2,…,n), которое ищется по таблице распределения Стьюдента при заданном уровне значимости α и числе степеней свободы k, равном k=m-n-1. В данном случае при уровне значимости α=0,05 и k=13-3-1=9 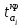 =2,26.
=2,26.
Таблица 18 – Рассчитанные опытные значения t – статистики Стьюдента
Если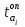 >
> 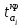
, то гипотеза о значимости коэффициента ai не отвергается, и соответствующая переменная xi остается в уравнении. В противном случае коэффициент ai считается незначимым и соответствующую ему переменную следует исключить из уравнения регрессии. Таким образом, сравнив полученные опытные значения с критическим
с критическим  , можно сделать вывод, что незначимых коэффициентов во всех четырех уравнениях нет.
, можно сделать вывод, что незначимых коэффициентов во всех четырех уравнениях нет.
Проверка значимости линейного уравнения множественной регрессии в целом
Если окажется, что при заданном уровне значимости α уравнение незначимо, то пользоваться им нельзя, а найденной зависимостью следует пренебречь.
Для проверки значимости уравнения регрессии используется опытная F-статистика Фишера:
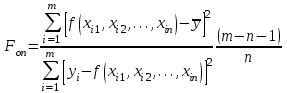 , (20)
, (20)
где m – объем выборки; n – число переменных в уравнении множественной регрессии; f(xi1, xi2, …, xin) – i-е расчетное значение переменной y;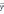
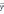 - среднее опытных значений случайной величины Y.
- среднее опытных значений случайной величины Y.
Полученные опытные значения
 критерия Фишера сравниваются с критическими значениями
критерия Фишера сравниваются с критическими значениями 
 =F(α;k1;k2) при выбранном уровне значимости α. Число степеней свободы k1 = m – n – 1, k2 = n.
=F(α;k1;k2) при выбранном уровне значимости α. Число степеней свободы k1 = m – n – 1, k2 = n.
При выбранном уровне значимости α=0,05 и числе степеней свободы k1 = 13 – 3 – 1= 9, k2 = 3
 =8,81
=8,81
Таблица 19 - Рассчитанные опытные значения критерия Фишера
При сравнении опытных значений критериев Фишера с критическим (при уровне значимости α=0,05 Fкр=8,81), все они удовлетворяют неравенству Fоп > Fкр и делается вывод, что с вероятностью p=1-α=0,95 все уравнения значимы, и мы получаем определенные основания доверять построенным уравнениям регрессии.
Оценка точности линейного уравнения множественной регрессии
Заключительная статистическая процедура – оценка точности построенных уравнений регрессии.
Оценка близости опытных значений yi случайной величины Y и ее расчетных значений f(xi), получаемых с помощью уравнения линейной регрессии, выполняется с помощью среднеквадратической погрешности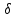 по следующей формуле:
по следующей формуле:
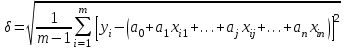 . (21)
. (21)
Таблица 20 - Результаты расчета среднеквадратичной погрешности уравнений
Расчет прогнозных значений
Для вычисления прогнозных значений воспользуемся данными из Программы социально-экономического развития республики. Целесообразно сравнить планируемые значения показателей с фактическими. Результаты сравнения представлены в таблицах № 21, 22.
Таблица 21 - Выполнение основных показателей Программы социально-экономического развития на 2012 – 2020 годы – Валовой региональный продукт
Таблица 22 - Выполнение основных показателей Программы социально-экономического развития на 2012 – 2020 годы – Инвестиции в основной капитал
Сравнение показало, что данными из Программы социально-экономического развития можно воспользоваться, так как плановые значения чаще ниже фактических.
Статистические, полученные расчетные и прогнозные данные представлены в таблице.
Таблица 23 - Статистические, расчетные и прогнозные показатели травматизма
Расчет риска травмирования
В настоящее время многие авторы отмечают, что поток несчастных случаев на производстве распределяется по дискретному пуассоновскому закону. Этот закон предполагает, что указанный поток обладает свойствами стационарности - интенсивность несчастных случаев не зависит от времени работы, ординарности - вероятность возникновения двух несчастных случаев и более на малом отрезке времени является величиной более высокого порядка малости по сравнению с вероятностью одного случая травмирования, отсутствием последействия - на любых двух не перекрещивающихся отрезках времени числа проявлений несчастных случаев независимы. Стационарность доказывается тем, что число случаев травмирования по годам меняется незначительно, ординарность - тем, что групповые несчастные случаи происходят крайне редко. Отсутствие последействия подтверждается тем, что число несчастных случаев, например, в декабре не зависит от того, сколько их было в предыдущем месяце, т.е. несчастные случаи появляются на оси времени по причинам, не зависимым от самих этих случаев. Вероятность несчастных случаев, по данным В.М. Минько, может быть представлена формулой
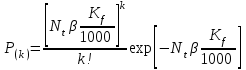 , (22)
, (22)
где Р(к) - вероятность k несчастных случаев, k = 0, 1, 2, 3, ...; N - число работающих; t - продолжительность работы, лет; β - повышающий коэффициент, использующийся тогда, когда есть основания считать данные о несчастных случаях заниженными. Имеются результаты исследований, из которых вытекает, что 1 < β < 5.
Выражение позволяет получать прогностические оценки различных событий, связанных с производственным травматизмом. Может быть получен и риск R травмирования
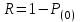 , (23)
, (23)
где Р(о) вычисляется по выражению. При k = 0 выражение получает вид
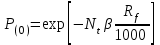 , (24)
, (24)
В выражение вместо коэффициента частоты можно ввести коэффициент смертности Кс.и., что позволяет записать
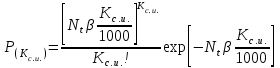 , (25)
, (25)
где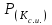 - вероятность Кс.и. (Кс.и. = 0, 1, 2, ...) несчастных случаев со смертельным исходом.
- вероятность Кс.и. (Кс.и. = 0, 1, 2, ...) несчастных случаев со смертельным исходом.
Таблица 24 – Риски травмирования
где
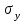 - среднее квадратичное отклонение для значений переменной y;
- среднее квадратичное отклонение для значений переменной y; 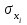 - среднее квадратичное отклонение для значений xi;
- среднее квадратичное отклонение для значений xi; 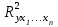 - коэффициент множественной детерминации для уравнения регрессии в целом;
- коэффициент множественной детерминации для уравнения регрессии в целом; 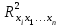 - коэффициент множественной детерминации, характеризующий зависимость между фактором xi и остальными факторами (x1, x2,…, xi-1, xi+1,…, xn)уравнения регрессии.
- коэффициент множественной детерминации, характеризующий зависимость между фактором xi и остальными факторами (x1, x2,…, xi-1, xi+1,…, xn)уравнения регрессии.Каждое из опытных значений статистики
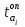 сравнивают с критическим значением
сравнивают с критическим значением 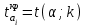 (i=1,2,…,n), которое ищется по таблице распределения Стьюдента при заданном уровне значимости α и числе степеней свободы k, равном k=m-n-1. В данном случае при уровне значимости α=0,05 и k=13-3-1=9
(i=1,2,…,n), которое ищется по таблице распределения Стьюдента при заданном уровне значимости α и числе степеней свободы k, равном k=m-n-1. В данном случае при уровне значимости α=0,05 и k=13-3-1=9 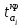 =2,26.
=2,26.Таблица 18 – Рассчитанные опытные значения t – статистики Стьюдента
| Показатель травмирования | 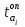 | ||
| a1 | a2 | a3 | |
| Кч | 7,32 | 7,35 | 6,45 |
| Кл | 8,17 | 8,67 | 7,23 |
| Кп.з. | 6,17 | 6,39 | 2,29 |
| Кт | 7,72 | 3,46 | 7,79 |
Если
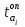 >
> 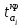
, то гипотеза о значимости коэффициента ai не отвергается, и соответствующая переменная xi остается в уравнении. В противном случае коэффициент ai считается незначимым и соответствующую ему переменную следует исключить из уравнения регрессии. Таким образом, сравнив полученные опытные значения
 с критическим
с критическим  , можно сделать вывод, что незначимых коэффициентов во всех четырех уравнениях нет.
, можно сделать вывод, что незначимых коэффициентов во всех четырех уравнениях нет.Проверка значимости линейного уравнения множественной регрессии в целом
Если окажется, что при заданном уровне значимости α уравнение незначимо, то пользоваться им нельзя, а найденной зависимостью следует пренебречь.
Для проверки значимости уравнения регрессии используется опытная F-статистика Фишера:
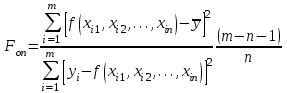 , (20)
, (20)где m – объем выборки; n – число переменных в уравнении множественной регрессии; f(xi1, xi2, …, xin) – i-е расчетное значение переменной y;
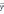
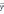 - среднее опытных значений случайной величины Y.
- среднее опытных значений случайной величины Y.Полученные опытные значения

 критерия Фишера сравниваются с критическими значениями
критерия Фишера сравниваются с критическими значениями 
 =F(α;k1;k2) при выбранном уровне значимости α. Число степеней свободы k1 = m – n – 1, k2 = n.
=F(α;k1;k2) при выбранном уровне значимости α. Число степеней свободы k1 = m – n – 1, k2 = n.При выбранном уровне значимости α=0,05 и числе степеней свободы k1 = 13 – 3 – 1= 9, k2 = 3

 =8,81
=8,81Таблица 19 - Рассчитанные опытные значения критерия Фишера
| Показатель травмирования | Fоп |
| Кч | 42,74 |
| Кл | 21,24 |
| Кп.з. | 20,8 |
| Кт | 22,4 |
При сравнении опытных значений критериев Фишера с критическим (при уровне значимости α=0,05 Fкр=8,81), все они удовлетворяют неравенству Fоп > Fкр и делается вывод, что с вероятностью p=1-α=0,95 все уравнения значимы, и мы получаем определенные основания доверять построенным уравнениям регрессии.
Оценка точности линейного уравнения множественной регрессии
Заключительная статистическая процедура – оценка точности построенных уравнений регрессии.
Оценка близости опытных значений yi случайной величины Y и ее расчетных значений f(xi), получаемых с помощью уравнения линейной регрессии, выполняется с помощью среднеквадратической погрешности
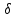 по следующей формуле:
по следующей формуле: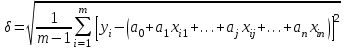 . (21)
. (21)Таблица 20 - Результаты расчета среднеквадратичной погрешности уравнений
| | 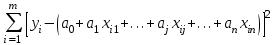 | 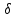 |
| Кч | 1,223 | 0,318 |
| Кл | 0,003 | 0,016 |
| Кп.з. | 10,984 | 0,955 |
| Кт | 111,746 | 3,045 |
Расчет прогнозных значений
Для вычисления прогнозных значений воспользуемся данными из Программы социально-экономического развития республики. Целесообразно сравнить планируемые значения показателей с фактическими. Результаты сравнения представлены в таблицах № 21, 22.
Таблица 21 - Выполнение основных показателей Программы социально-экономического развития на 2012 – 2020 годы – Валовой региональный продукт
| Год | Факт, млрд.руб. | План, млрд.руб. |
| 2012 | 140 | 120,7 |
| 2013 | 164,8 | 132,9 |
| 2014 | 205,8 | 145,9 |
| 2015 | 240,3 | 159,4 |
| 2016 | 226,1 | 174,1 |
| 2017 | 264,5 | 243,8 |
| 2018 | 318,8 | 264,5 |
| 2019 | 335,4 | 346,6 |
| 2020 | 404,8 | 414,5 |
Таблица 22 - Выполнение основных показателей Программы социально-экономического развития на 2012 – 2020 годы – Инвестиции в основной капитал
| Год | Факт, млрд.руб. | План, млрд.руб. | ||
| 2012 | 26,9 | 17,7 | ||
| 2013 | 34,3 | 20,1 | ||
| 2014 | 44,5 | 22,9 | ||
| 2015 | 49,9 | 26,0 | ||
| 2016 | 41,3 | 29,1 | ||
| 2017 | 42,3 | 40,1 | ||
| 2018 | 60,9 | 50,2 | ||
| 2019 | 57,2 | 65,6 | ||
| 2020 | 71,8 | 72,3 | ||
Сравнение показало, что данными из Программы социально-экономического развития можно воспользоваться, так как плановые значения чаще ниже фактических.
Статистические, полученные расчетные и прогнозные данные представлены в таблице.
Таблица 23 - Статистические, расчетные и прогнозные показатели травматизма
| Год | Кч | Кч прог. | Кл | Кл прог | Кп.з. | Кп.з.прог | Кт | Кт прог |
| 2004 | 6,170 | 5,543 | 0,124 | 0,107 | 1,579 | 1,598 | 23,000 | 23,309 |
| 2005 | 5,586 | 5,448 | 0,103 | 0,106 | 1,474 | 1,525 | 23,500 | 23,978 |
| 2006 | 5,273 | 5,334 | 0,118 | 0,104 | 1,613 | 1,493 | 25,600 | 25,931 |
| 2007 | 5,012 | 5,192 | 0,081 | 0,100 | 1,688 | 1,475 | 24,417 | 25,136 |
| 2008 | 4,689 | 4,761 | 0,085 | 0,096 | 1,449 | 1,353 | 24,660 | 26,106 |
| 2009 | 4,308 | 4,454 | 0,087 | 0,090 | 1,313 | 1,301 | 26,121 | 29,03 |
| 2010 | 3,872 | 3,984 | 0,103 | 0,082 | 1,062 | 1,219 | 35,826 | 32,353 |
| 2011 | 3,492 | 3,582 | 0,052 | 0,072 | 1,171 | 1,158 | 43,105 | 35,621 |
| 2012 | 3,089 | 3,792 | 0,062 | 0,076 | 1,237 | 1,154 | 39,604 | 35,45 |
| 2013 | 3,121 | 3,121 | 0,041 | 0,040 | 1,369 | 1,380 | 38,899 | 39,261 |
| 2014 | 3,084 | 2,754 | 0,047 | 0,058 | 1,150 | 0,917 | 41,300 | 42,047 |
| 2015 | 2,500 | 2,624 | 0,034 | 0,055 | 0,621 | 0,834 | 40,665 | 44,417 |
| 2016 | 2,203 | 1,874 | 0,070 | 0,044 | 0,529 | 0,624 | 46,544 | 46,809 |
| 2017 | - | 1,812 | - | 0,033 | - | 0,714 | - | 47,940 |
| 2018 | - | 1,496 | - | 0,027 | - | 0,637 | - | 50,028 |
| 2019 | - | 1,179 | - | 0,020 | - | 0,561 | - | 52,116 |
| 2020 | - | 0,862 | - | 0,014 | - | 0,484 | - | 54,204 |
Расчет риска травмирования
В настоящее время многие авторы отмечают, что поток несчастных случаев на производстве распределяется по дискретному пуассоновскому закону. Этот закон предполагает, что указанный поток обладает свойствами стационарности - интенсивность несчастных случаев не зависит от времени работы, ординарности - вероятность возникновения двух несчастных случаев и более на малом отрезке времени является величиной более высокого порядка малости по сравнению с вероятностью одного случая травмирования, отсутствием последействия - на любых двух не перекрещивающихся отрезках времени числа проявлений несчастных случаев независимы. Стационарность доказывается тем, что число случаев травмирования по годам меняется незначительно, ординарность - тем, что групповые несчастные случаи происходят крайне редко. Отсутствие последействия подтверждается тем, что число несчастных случаев, например, в декабре не зависит от того, сколько их было в предыдущем месяце, т.е. несчастные случаи появляются на оси времени по причинам, не зависимым от самих этих случаев. Вероятность несчастных случаев, по данным В.М. Минько, может быть представлена формулой
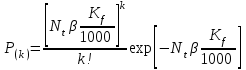 , (22)
, (22)где Р(к) - вероятность k несчастных случаев, k = 0, 1, 2, 3, ...; N - число работающих; t - продолжительность работы, лет; β - повышающий коэффициент, использующийся тогда, когда есть основания считать данные о несчастных случаях заниженными. Имеются результаты исследований, из которых вытекает, что 1 < β < 5.
Выражение позволяет получать прогностические оценки различных событий, связанных с производственным травматизмом. Может быть получен и риск R травмирования
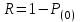 , (23)
, (23)где Р(о) вычисляется по выражению. При k = 0 выражение получает вид
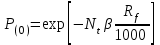 , (24)
, (24)В выражение вместо коэффициента частоты можно ввести коэффициент смертности Кс.и., что позволяет записать
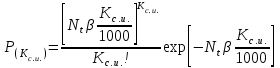 , (25)
, (25)где
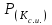 - вероятность Кс.и. (Кс.и. = 0, 1, 2, ...) несчастных случаев со смертельным исходом.
- вероятность Кс.и. (Кс.и. = 0, 1, 2, ...) несчастных случаев со смертельным исходом.Таблица 24 – Риски травмирования