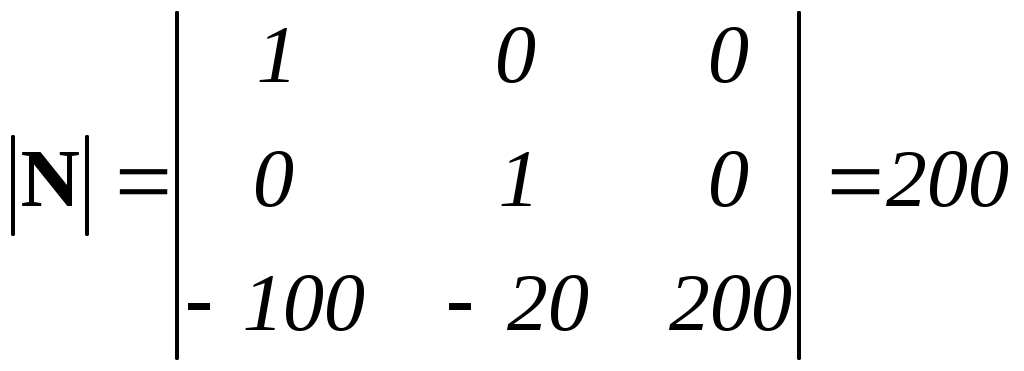ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 86
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 11.1 - Схема оценки знаний студентов
| № | Вид занятий и работ обучающихся | Количество баллов min/max |
| I | Текущий контроль: Практические занятия Лабораторные занятия Самостоятельная работа обучающегося | 50/100 50/100 50/100 |
| | Итого: ТКср | 50/100 |
| II | Итоговый контроль: экзамен | 50/100 |
| | Итого за предмет | 50/100 |
Окончательная оценка знаний студентов, итоговый рейтинг (И), выставляется по шкале оценки знаний студентов, основанной на 100-бально-рейтинговой системе (БРС). Итоговый балл по дисциплине в процентном содержании определяется по формуле: И% = ТКср
Таблица 11.2 – Оценка знаний обучающихся на экзамене
| № | Экзаменационная оценка | Оценка в баллах (за каждое выполненное задание) |
| 1 | Текущий контроль | 50/100 |
| 2 | Итоговый контроль | 50/100 |
| | Итого (среднее): | 50/100 |
Таблица 11.3 - Шкала оценки знаний обучающихся
Балльно-рейтинговая буквенная система оценки учета учебных достижений, обучающихся с переводом их в традиционную шкалу оценок и ECTS (иситиэс)
| Оценка по буквенной системе | Цифровой эквивалент | Баллы (%-ное содержание) | Оценка по традиционной системе |
| А | 4,0 | 95-100 | Отлично |
| А- | 3,67 | 90-94 | |
| В+ | 3,33 | 85-89 | Хорошо |
| В | 3,0 | 80-84 | |
| В- | 2,67 | 75-79 | |
| С+ | 2,33 | 70-74 | |
| С | 2,0 | 65-69 | Удовлетворительно |
| С- | 1,67 | 60-64 | |
| D+ | 1,33 | 55-59 | |
| D- | 1,0 | 50-54 | |
| FX | 0,5 | 25-49 | Неудовлетворительно |
| F | 0 | 0-24 |
В случае получения «FX» обучающейся имеет возможность пересдать итоговый контроль без повторного прохождения программы учебной дисциплины (на бесплатной основе). В период промежуточной аттестации обучающегося допускается пересдача экзамена (FX) по учебной дисциплине не более двух раз. В случае получения в третий раз оценки (FX), обучающийся отчисляется из вуза и теряет возможность записываться на данную дисциплину повторно.
В случае получения «F» обучающийся повторно записывается на данную учебную дисциплину, посещает все виды учебных занятий (летний семестр), выполняет все виды учебной работы согласно программе и пересдает итоговый контроль.
Изменения внесены согласно Методической комиссии протокол 6 от 31.03.2020
Форма карты учебно-методической обеспеченности для дисциплин
Карта учебно-методической обеспеченности дисциплины Системы автоматизации и управления технологических процессов»
| Ф.И.О. автора | Наименование учебно-методической литературы | Издательство, год издания | Количество экземпляров | |
| в библиотеке | на кафедре | |||
| Основная литература | ||||
| В.А. Веникова | Электрические системы. Математические задачи электроэнергетики : учебник для студентов вузов | М. : Высш. школа, 1981. – 288 с. | 1 | Электронный вариант |
| Ерофеев А.А. | Теория автоматического управления | учеб. для вузов. – 2-е изд., перераб. и доп. – СПб. : Политехника, 2005. – 302 с. | | Электронный вариант |
| Бороденко В.А. | Практический курс теории линейных систем автоматического регулирования. | Павлодар : Кереку, 2007. – 260 с. | | Электронный вариант |
| Дополнительная литература | ||||
| Бесекерский, В. А. | Теория систем автоматического регулирования [Текст] : научное издание | 3-е изд., испр. . - М. : Наука (Гл. ред.физико-матем. лит-ры), 1975. - 768 с. | 1 | Электронный вариант |
| Бороденко В.А., Жантлесова А.Б.. | Сызықты автоматты реттеу жүйесінің теориясы. Теория линейных систем автоматического регулирования. Практикум к лабораторным работам по дисциплине «ТАУ». | Павлодар : Кереку, 2007. – 180 с. | | Электронный вариант |
| Бороденко В.А., Жантлесова А.Б.. | Бейсызықты автоматты реттеу жүйесінің теориясы. Теория нелинейных систем автоматического регулирования. Практикум к лабораторным работам по дисциплине «ТАУ». | Павлодар : Кереку, 2007. – 180 с. | | Электронный вариант |
Преподаватель ____________ Жантлесова А.Б.
Заведующий кафедрой ___________ Сарсикеев Е.Ж.
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РЕСПУБЛИКИ КАЗАХСТАН
«КАЗАХСКИЙ АГРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С. СЕЙФУЛЛИНА»
КРАТКИЙ КУРС ЛЕКЦИЙ
по дисциплине «Системы автоматизации и управления технологических процессов»
для образовательной программы: Электроснабжение, Электрические сети, Электроэнергетика
Нур-Султан 2021
Отдельно вставлен, так как не сохраняеться в платонусе
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РЕСПУБЛИКИ КАЗАХСТАН
«КАЗАХСКИЙ АГРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С. СЕЙФУЛЛИНА»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ ЗАНЯТИЙ
по дисциплине «Системы автоматизации и управления технологических процессов»
для образовательной программы: Электроснабжение, Электрические сети, Электроэнергетика
Нур-Султан 2021
Отдельно вставлен, так как не сохраняеться в платонусе
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РЕСПУБЛИКИ КАЗАХСТАН
«КАЗАХСКИЙ АГРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С. СЕЙФУЛЛИНА»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ СРО
по дисциплине «Системы автоматизации и управления технологических процессов»
для образовательной программы: Электроснабжение, Электрические сети, Электроэнергетика
Нур-Султан 2021
Задание
Для объекта управления (рисунок 1), используя данные своего варианта (таблица 1):
- описать объект управления в пространстве состояний;
- оценить устойчивость объекта управления;
- оценить управляемость объекта управления;
- оценить наблюдаемость объекта управления;
- выбрать параметры наблюдателя полного порядка;
- выбрать параметры модального регулятора;
- составить схему системы управления, произвести проверку.
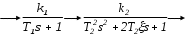
Рисунок 1
Таблица 1
| Параметр | Вариант | |||||||||
| 1, 11 | 2, 12 | 3, 13 | 4, 14 | 5, 15 | 6, 16 | 7, 17 | 8, 18 | 9, 19 | 10, 20 | |
| k1 | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 |
| k2 | 10,00 | 5,00 | 3,33 | 2,50 | 2,00 | 1,67 | 1,43 | 1,25 | 1,11 | 1,00 |
| T1 | Равно номеру первой буквы фамилии в алфавите | |||||||||
| T2 | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 |
| ξ | 0,45 | 0,50 | 0,55 | 0,60 | 0,65 | 0,70 | 0,75 | 0,80 | 0,85 | 0,90 |
| tрег | 12,00 | 11,00 | 10,00 | 9,00 | 8,00 | 7,00 | 6,00 | 5,00 | 4,00 | 3,00 |
| σ | 0,25 | 0,25 | 0,20 | 0,20 | 0,15 | 0,15 | 0,10 | 0,10 | 0,05 | 0,05 |
Методический пример
1 Описание объекта управления в пространстве состояний
О
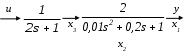
бъект управления состоит из апериодического и колебательного звеньев (рисунок 2) с параметрами, соответствующими заданному варианту.
Рисунок 2
Входное воздействие u(t), регулируемая величина y(t). Назначаем переменные состояния методом фазовых переменных, начиная с выхода системы и увеличивая индексы при движении по главной прямой связи к входу системы. Звену второго порядка соответствует внутренняя переменная x2.
Нормируем передаточные функции звеньев по коэффициенту при старшей степени s в знаменателе.
Составляем уравнения состояния и наблюдения. Уравнение состояния
уравнение наблюдения
Отсюда описание системы в пространстве состояний
где матрицы собственных коэффициентов А, коэффициентов входов b, коэффициентов выходов с и коэффициентов обходов d равны соответственно
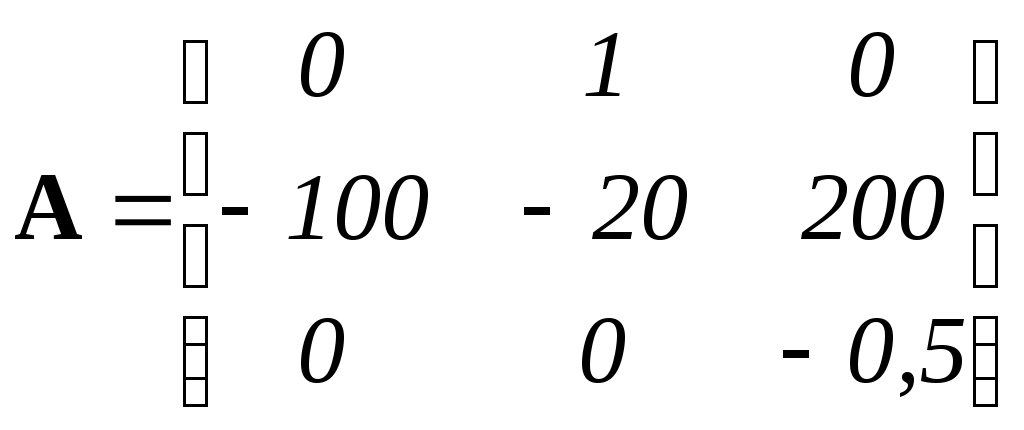 ;
; 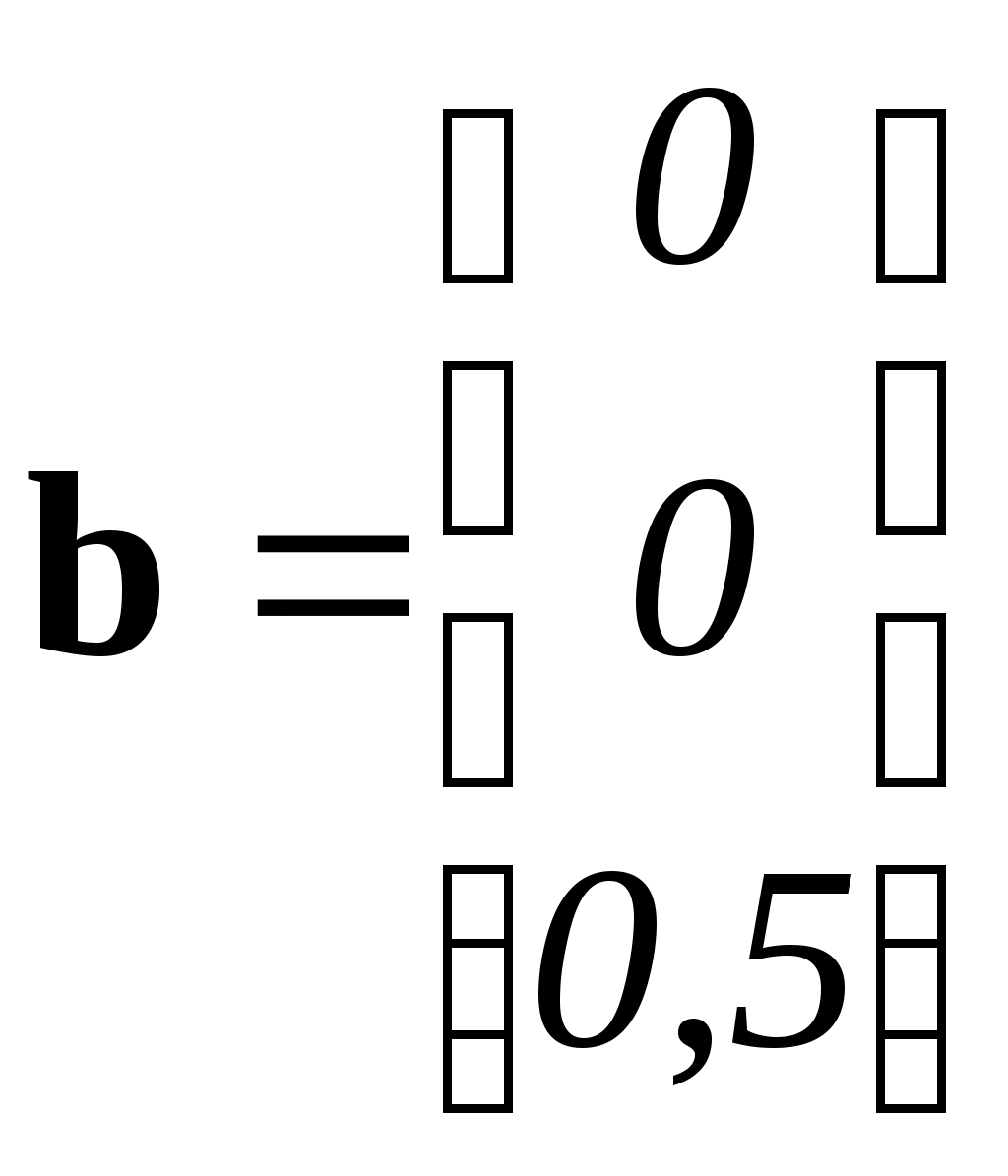 ;
; 2 Проверка устойчивости объекта управления
Для проверки устойчивости объекта составляем его характеристическую матрицу [s*1 - A], где s – комплексная переменная Лапласа, 1 – единичная матрица, порядок которой равен порядку системы, т.е. n = 3.
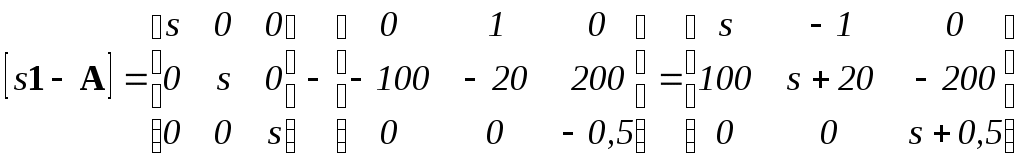 .
.Вычисляем характеристический полином объекта (определитель характеристической матрицы)
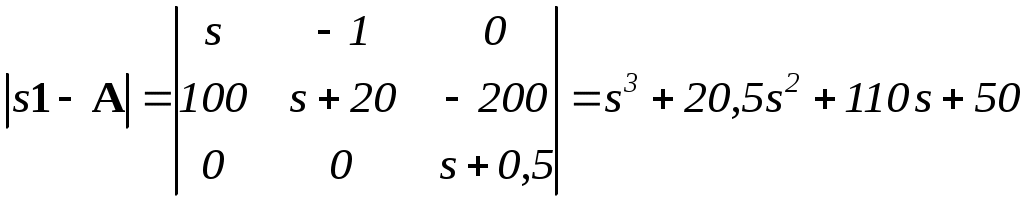 .
.Для устойчивости системы третьего порядка по критерию Гурвица необходимо и достаточно, чтобы все коэффициенты характеристического полинома были положительными, а диагональные миноры первого и второго порядка были больше нуля.
Так как минор первого порядка Δ1 = 20,5 больше нуля, минор второго порядка Δ2 = 20,5*110 - 50*1 = 2205 больше нуля и все коэффициенты характеристического полинома положительны, объект управления устойчив.
3 Проверка управляемости объекта управления
Составляем матрицу управляемости объекта, для чего вычисляем матрицы Ab, A2b и добавляем их справа к матрице b
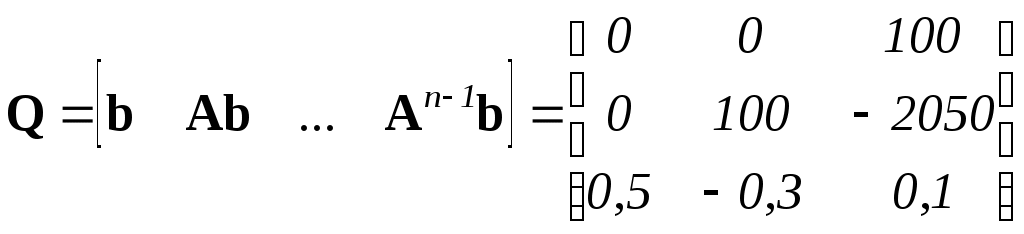 .
.Вычисляем определитель матрицы управляемости
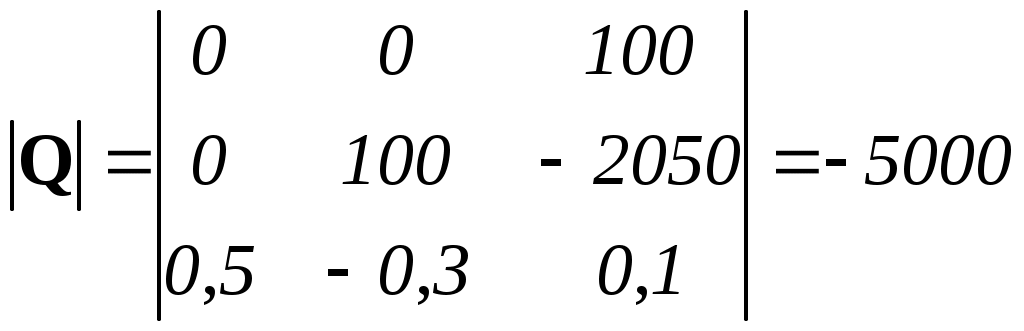 .
.Поскольку главный определитель матрицы не равен нулю, ее ранг равен порядку системы n = 3 и, следовательно, объект полностью управляем.
4 Проверка наблюдаемости объекта управления
Составляем матрицу наблюдаемости объекта, для чего вычисляем матрицы Aс, A2с и добавляем их снизу к матрице с
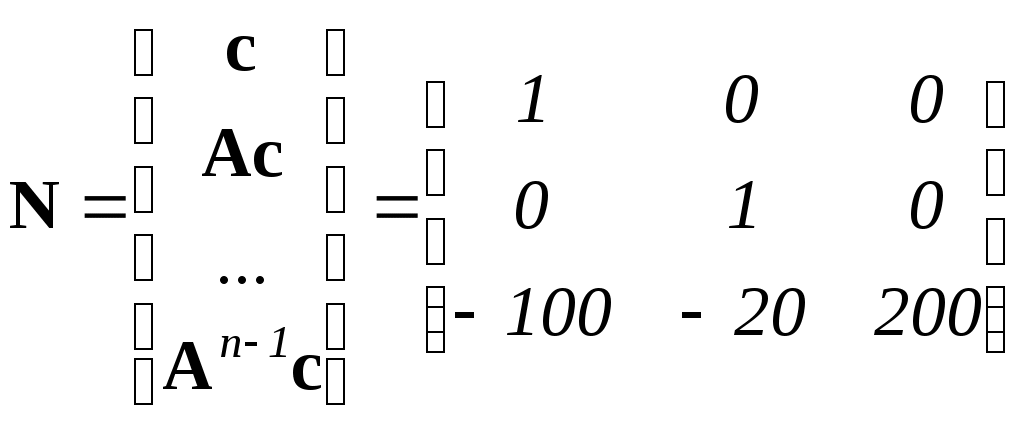 .
.Вычисляем определитель матрицы наблюдаемости