Файл: Решение функциональных и вычислительных задач средствами пакетов прикладных программ Mathcad и электронных таблиц Excel.doc

Федеральное агентство по образованию

Хакасский технический институт – филиал КГТУ

Кафедра прикладной информатики

Расчетно-пояснительная записка

К курсовому проекту по дисциплине «Информатика»

Тема: Решение функциональных и вычислительных задач средствами пакетов прикладных программ MathCAD и электронных таблиц Excel

Вариант32

Выполнил:

студент группы 34-2

Липнягова Наталья
Проверил:

ассистент кафедры

прикладной информатики

Медведева Т.М.

Абакан, 2005

Содержание

Введение___________________________________________________________3

Решение нелинейных уравнений_______________________________________5

Решение системы нелинейных уравнений_______________________________6

Решение системы линейных алгебраических уравнений___________________8

Интерполирование. Аппроксимация__________________________________ 12

Решение дифференциальных уравнений_______________________________ 17

Линейное программирование_________________________________________18

Трендовый анализ__________________________________________________21

Создание электронной таблицы_______________________________________23

Заключение_______________________________________________________25

Список литературы_________________________________________________27

Введение
Фундаментальной чертой цивилизации является рост производства

, потребления и накопления информации во всех отраслях челове-

ческой деятельности. Вся жизнь человека, так или иначе, связана с

получением, накоплением и обработкой информации. Что бы человек

не делал: читает ли он книгу, смотрит ли он телевизор, разговари-

вает ли - он постоянно и непрерывно получает и обрабатывает ин-

формацию.

Увеличение информации и растущий спрос на нее обусловили по-

явление отрасли, связанной с автоматизацией обработки информации

- ИНФОРМАТИКИ.

В наше время существует множество всевозможных программ обработки информации.

В этой работе представлены две такие программы. Это EXCEL и Mathcad.

Mathcad – это пакет прикладных программ, для решения математических, физических, экономических, систематических им других видов задач.

Это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования. Название системы происходит от двух слов – MATHematica ( математика) и CAD ( Computer Aided Design – системы автоматического проектирования, или САПР). Так что вполне правомерно считать Mathcad математическими САПР.

---

Сегодня различные версии Mathcad являются математически ориентированными универсальными системами. Помимо собственно вычислений, как численных, так и аналитических, они позволяют с блеском решать сложные оформительские задачи, которые с трудом даются популярным текстовым редакторам или электронным таблицам. С помощью Mathcad можно, например, готовить статьи, книги, диссертации, дипломные и курсовые проекты не только с качественными текстами разного стиля, но и с легко осуществляемым набором самых сложных математических формул, изысканным графическим представлением результатов вычислений и многочисленными «живыми» примерами. А применение библиотек и пакетов расширения обеспечивает профессиональную ориентацию Mathcad на любую область науки, техники и образования.

Mathcad содержит более ста операторов и функций предназначенных для численного и символьного решения задач, инструменты построения графиков различных типов в декартовой, полярной системе координат и т.д.

К важным достоинствам новых версий Mathcad относятся настройка под любой мало-мальски известный тип печатающих устройств, богатый набор шрифтов, возможность использования всех инструментов Windows, прекрасная графика и современный многооконный интерфейс. В новые версии Mathcad включены эффектные средства оформления документов в цвете, возможность создания анимационных ( движущихся) графиков и звукового сопровождения. Предусмотрена и возможность объединения и с другими математическими и графическими системами для решения особо сложных задач. Отсюда и название таких систем – интегрированные системы.

В конце 2000 года выпущена новейшая версия системы – Mathcad 2001. В ней существенно повышены скорость вычислений и удобства работы, введен рад новых возможностей.

Как интегрированная система Mathcad содержит следующие основные компоненты:

Редактор документов – редактор с возможностью вставки математических выражений, шаблонов графиков и текстовых комментариев;

Центр ресурсов – интегратор ресурсов системы;

Электронные книги – электронные книги с описанием типовых расчетов в различных областях науки и техники;

Справочная система – система для получения справочных данных по тематическому и индексному каталогу, а также для поиска нужных данных по ключевому слову или фразе.

А также «быстрые шпаргалки» и броузер Интернета.

Возможности EXCEL очень высоки. В пакете Excel имеется программа проверки орфографии текстов,

---

находящихся в ячейках рабочего листа, диаграммах или текстовых полях. Функции призваны облегчить работу при создании и взаимодействии электронными таблицами. Простейшим примером выполнения расчетов является операция сложения. Работать с электронными таблицами само по себе большое удовольствие, но если бы удалось превратить сухие столбцы чисел в наглядные диаграммы и графики. Такую возможность дает Excel. Для оформления документов Excel предлагает кроме графиков и диаграмм возможность создавать другие графические объекты, например, вычерчивать на экране, а потом распечатывать прямоугольники, эллипсы, прямые и кривые линии, дуги и др. Можно также выполнить рисунки с помощью отдельных графических объектов, что никто не будет подозревать, что они выполнены с помощью Excel, а не специально графического редактора. Обработка текста, управление базами данных - программа настолько мощна, что во многих случаях превосходит специализированные программы-редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, чем заставить применять на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей EXCEL тяжело достичь.
Задание 1. Решение нелинейных уравнений.

1. 
   Решение нелинейного уравнения графически с точностью до 0,001.
   

Для того, чтобы решить уравнение с данной точностью нужно задать интервал изменения х, с шагом 0,001:


где -1 – начальное значение переменной х, 1 – конечное значение переменной х, 0.0001 – шаг.

Зададим саму функцию

Построим график:



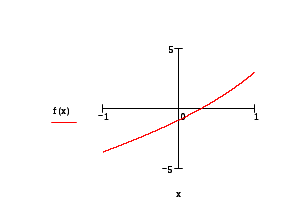
С помощью трассировки найдем точку пересечения графика с осью ох. Координат х будет являться решением этого уравнения:

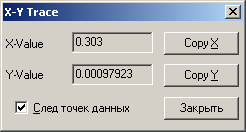
Ответ: х = 0,303

2. 
   Решение с помощью solve.
   

Символьный оператор solve можно взять на панели ключевых операторов.

---

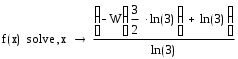
где х – имя переменной, относительно которой решается данное уравнение.
Решение с помощью root.
Зададим начальное приближение:



Зададим функцию:



Ответ: х = 0,303
Мы решили систему нелинейного уравнения разными способами и во всех случаях получили одинаковый ответ, следовательно, решения проведены, верно.

Проверка



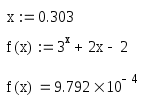
Ответ приблизительно равен о, следовательно, решение верно.
Задание 2. Решение системы нелинейных уравнений.

1. 
   Графически с точностью до 0,001
   

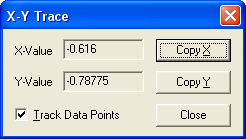
Выразим из уравнения у, и запишем в виде у(х):



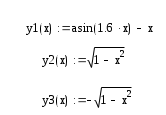
Построим график, и с помощью трассировки найдем точки пересечения графика с осями:

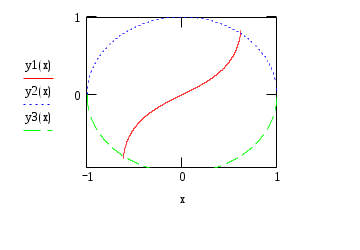
Для первой точки:

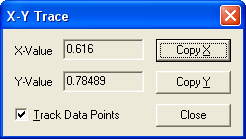
Для второй точки:

2. 
   Графически с помощью Given и Find.
   

Зададим начальное приближение х и у:



Зададим систему уравнений:




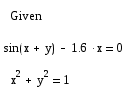
Для второго корня:



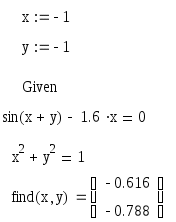
Значок «жирное» равно можно взять на булевой панели или нажав клавиши

₊
Ctrl

=


Сделаем проверку:


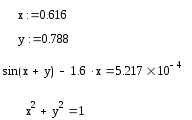
Мы решили систему нелинейных уравнений разными способами и получили примерно одинаковые ответы, следовательно, решения верны.
Задание 3. Решение системы линейных алгебраических уравнений.

1. 
   Решение СЛАУ с помощью given(дано) и find(найти).
   

---

Сделаем проверку:

2. 
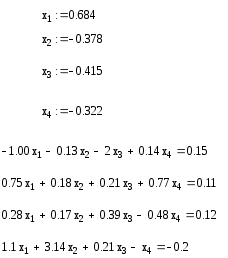
   С помощью функции lsolve.
   

Задаем матрицу А, состоящую из коэффициентов при неизвестных, и матрицу В, состоящую из свободных коэффициентов.

3. 
   С помощью обратной матрицы.
   

Задаем матрицу А и В :



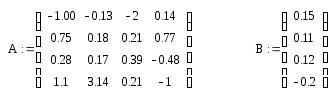
по формуле вычисляем:


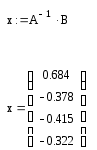
И делаем проверку:



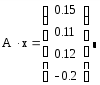
В результате получилась матрица В, следовательно, расчет проведен правильно.

4. 
   По формулам Крамера.
   

Вводим матрицы А и В:

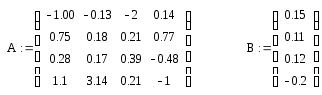
Вычисляем главный определитель из коэффициентов матрицы А:



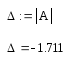
Главный определитель отличен от нуля, следовательно, существует единственное решение.

Вычислим определитель А1 заменив первый столбец матрицы А, столбцом матрицы В. И найдем значение 1




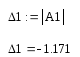
Теперь мы можем найти значение x₁:



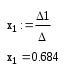
Аналогично находим x₂, x₃, x₄:

5. 
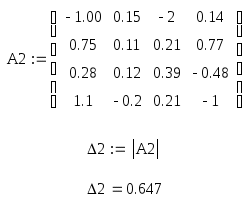
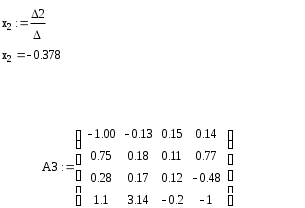
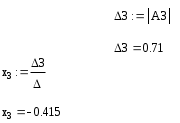
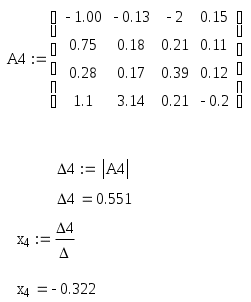
   Методом Гаусса.
   

С помощью функции augment формируем расширенную матрицу АB:



Обращаемся к методу Гаусса с помощью функции rref:



Последний столбец является решением данной СЛАУ.

---