Файл: Решение функциональных и вычислительных задач средствами пакетов прикладных программ Mathcad и электронных таблиц Excel.doc

С помощью функции submatrix выделим нужный нам столбец элементов, где Ar – данная матрица; 0 и 3 – начальный и конечный номер строки выделяемого блока соответственно; 4и 4 – начальный и конечный номер столбца выделяемого блока соответственно.



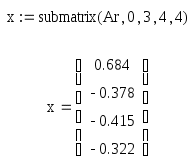
Мы решили СЛАУ разными способами, и видим, что результаты получились во всех случаях одинаковыми, следовательно, все решено, верно

Задание 4. Интерполирование. Аппроксимация.
Найти приближенное значение функции при заданном аргументе.

Зададим значения:

1. 
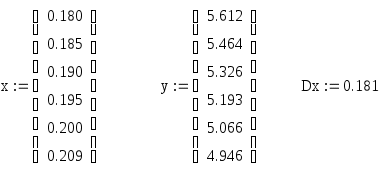
   С помощью линейной интерполяции.
   

Интерполирование – нахождение приближенной функции ( или замена таблично-заданной функции, приближенной функцией в виде формулы.

2. 
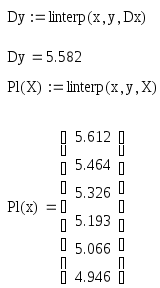
   С помощью параболического сплайна.
   

Сплайн – математическая модель гибкого тонкого стержня из упругого материала.

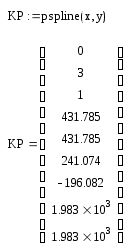
где КР – Вектор второй производной при приближении в угловых точках к прямой линии кубического полинома.

Найдем значение в точке Dx:



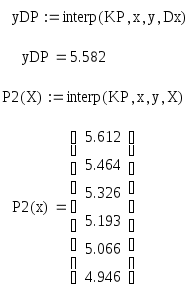
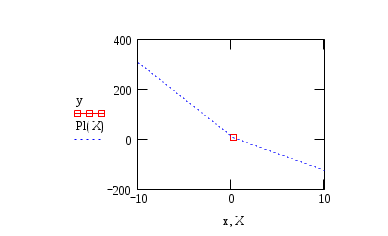
Построим график:

3. 
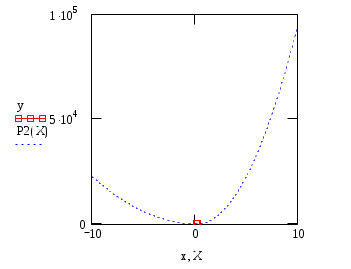
   С помощью линейной аппроксимации.
   

Порядок полинома равен 1:

4. 
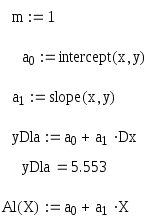
   Методом наименьших квадратов.
   

Суть метода наименьших квадратов: сумма квадратов разностей аппроксимй функцией и функцией заданной таблично, должна быть минимальной.

Зададим значения:

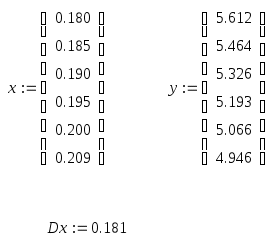
Порядок трем:



Функция rows вычисляет количество строк х

---

Запишем матрицы А и b:














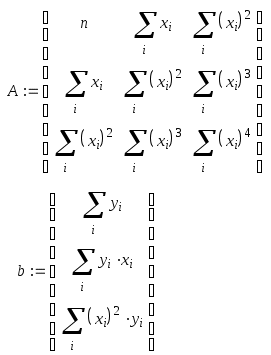
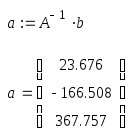
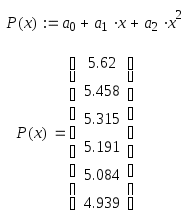
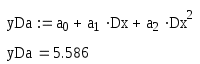
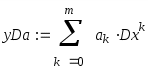
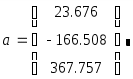
Рассчитаем погрешность:


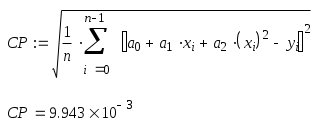
СР < 1, следовательно найдено все верно.

Построим график:

5. 
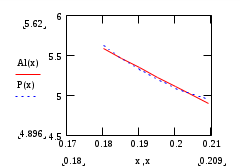
   С помощью полиномиальной регрессии.
   

Функция rows вычисляет количество строк х



Функция regress возвращает вектор чисел в котором имеются коэффициенты





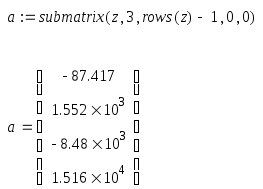
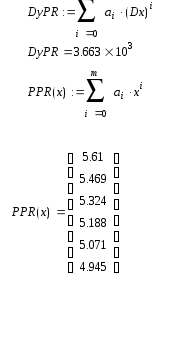
Рассчитаем погрешность:


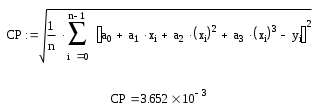
Результат получился меньше единицы, следовательно, решение верно.

Построим график:



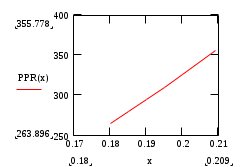
Задание 5. Решение дифференциальных уравнений.
Решить дифференциальное уравнение методом Рунге-Кутта.






где у1 – вектор начальных условий; 0,5 – начальное значение переменной х; 1,5 – конечное значение переменной х; 20 – число узлов на отрезке [0,5;1,5]; f – вектор, содержащий правые части разрешенного, относительно старшей производной дифференцированного уравнения.

---

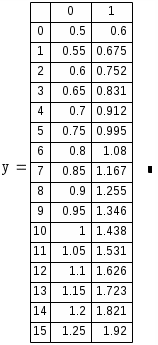
Построим график:

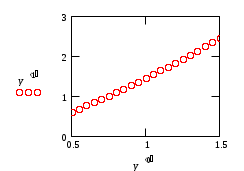
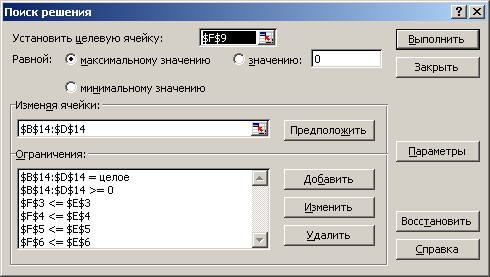
Задание 6. Линейное программирование.

Решить задачу линейного программирования средствами пакетов прикладных программ Mathcad и Excel.

В электронной таблице Excel представить две таблицы: одну срезультатами, другую с формулами.
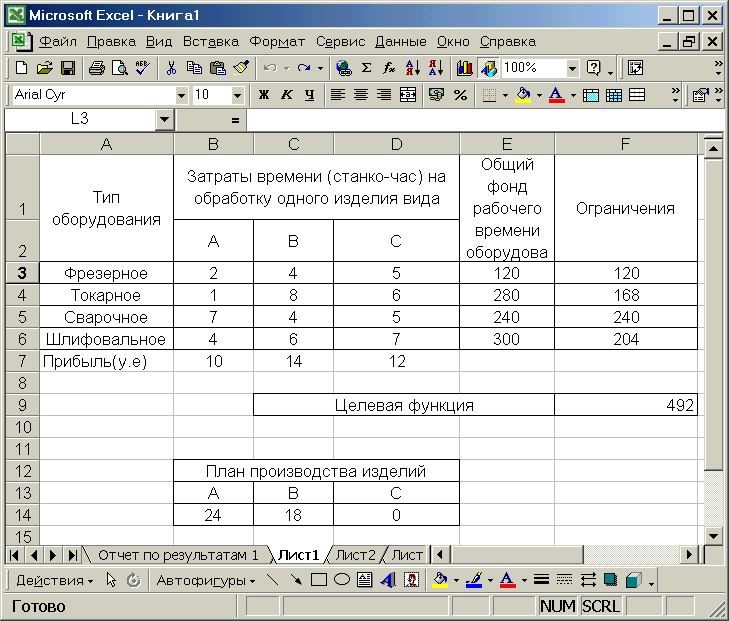
Задача: Для изготовления трех видов изделий А, В, С используется токарное, фрезерное, шлифовальное и сварочное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования приведены в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия каждого вида.

Тип оборудования	Затраты времени (станко-час) на обработку одного изделия вида			Общий фонд рабочего времени оборудования (ч)	Ограничения
	А	В	С
Фрезерное	2	4	5	120	120
Токарное	1	8	6	280	168
Сварочное	7	4	5	240	240
Шлифовальное	4	6	7	300	204
Прибыль(у.е)	10	14	12

Требуется определить, сколько изделий, и какого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной.



Ячейка__Имя__Исходно__Результат'>Ячейка F3: =B3*B14+C3*C14+D14*D3

Ячейка F4: =B4*B14+C4*C14+D4*D14

Ячейка F5: =B5*B14+C5*C14+D5*D14

Ячейка F6: =B6*B14+C6*C14+D6*D14

Ячейка F9: =B7*B14+C7*C14+D7*D14

Мы задали ряд у с именем $B$2 и значением $B$3:$B$8, а также подписали ось х: $A$3:$A$8 и построили линию тренда полиномиального вида.

---

Выполним отчет по результатам

Целевая ячейка (Максимум)
	Ячейка	Имя	Исходно	Результат
	$F$9	Целевая функция Ограничения	0	492

Изменяемые ячейки
	Ячейка	Имя	Исходно	Результат
	$B$14	А	0	24
	$C$14	В	0	18
	$D$14	С	0	0

Ограничения
	Ячейка	Имя	Значение	формула	Статус	Разница
	$F$4	Токарное Ограничения	168	$F$4<=$E$4	не связан.	112
	$F$5	Сварочное Ограничения	240	$F$5<=$E$5	связанное	0
	$F$6	Шлифовальное Ограничения	204	$F$6<=$E$6	не связан.	96
	$F$3	Фрезерное Ограничения	120	$F$3<=$E$3	связанное	0
	$B$14	А	24	$B$14=целое	связанное	0
	$C$14	В	18	$C$14=целое	связанное	0
	$D$14	С	0	$D$14=целое	связанное	0
	$B$14	А	24	$B$14>=0	не связан.	24
	$C$14	В	18	$C$14>=0	не связан.	18
	$D$14	С	0	$D$14>=0	связанное	0

---

Составим математическую модель задачи.
Пусть х1 – количество изделий, требуемое для получения максимальной прибыли, вида А

х2 – количество изделий, требуемое для получения максимальной прибыли, вида В

х3 – количество изделий вида, требуемое для получения максимальной прибыли, вида С

Зададим целевую функцию.



Начальное значение изделий принимаем, равным нулю:





Также эти значения не могут быть отрицательными:



У нас есть ограничения по времени 


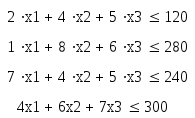Воспользуемся функцией Maximize: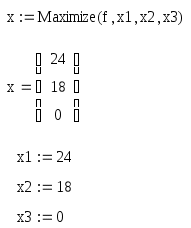



Проверим не выходят ли наши значения за рамки ограничений:


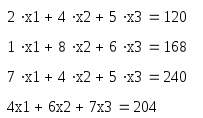
И посчитаем максимальную прибыль:



Мы нашли прибыль от реализации полученного количества товаров.

Данные, полученные при решении задачи с помощью линейного программирования, и с помощью математической модели совпадают, следовательно, расчеты проведены, верно.
Задание 7. Трендовый анализ.
Построить линию тренда и найти приближенную функцию.




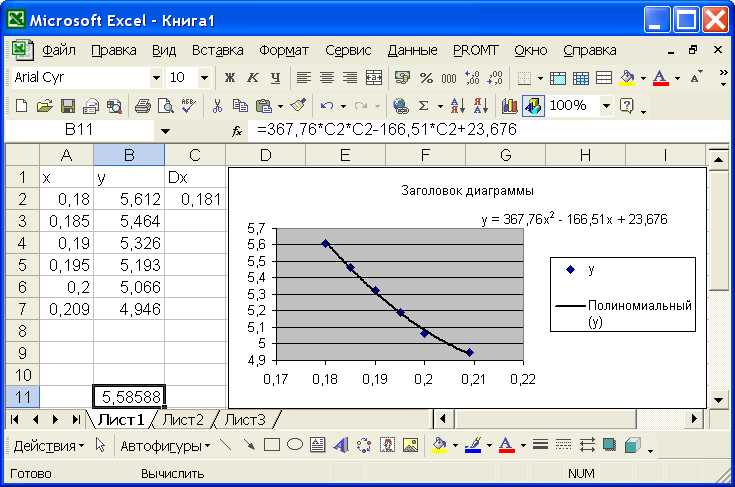
Задание 8.Создание электронной таблицы.
Таблица с формулами.

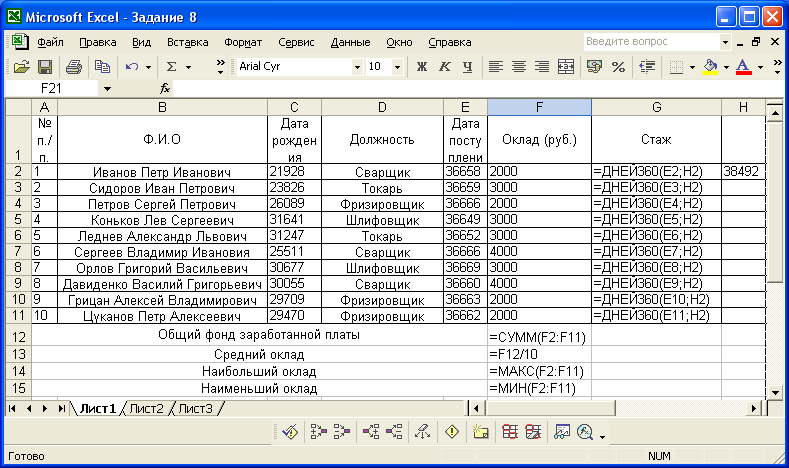
Таблица с результатами.

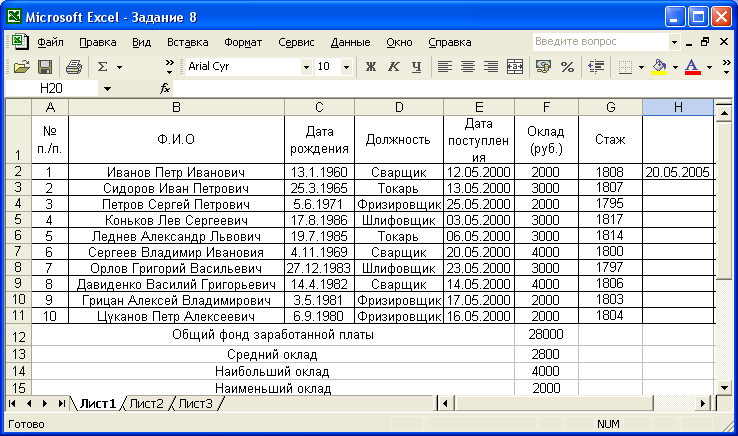
С помощью функции СУММ мы посчитали общий фонд заработной платы: =СУММ(F2:F11)

С помощью функции МАКС мы посчитали наибольший оклад: =МАКС(F2:F11)

С помощью функции МИН мы посчитали наименьший оклад: =МИН(F2:F11)

С помощью функции ДНЕЙ360 мы посчитали стаж каждого работника: =ДНЕЙ360(E2;H2).

Заключение

---