Файл: Даны вершины А(5 3), В(11 9), С(4 15) треугольника авс.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 272

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Частное профессиональное образовательное учреждение

«ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»
Практическое задание

по


дисциплине


Выполнил(а) студент(ка)





фамилия имя отчество

Идентификационный номер:





































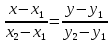
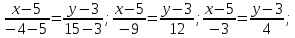
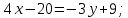
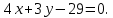
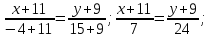
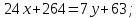
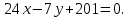
Пермь 20___Задание №1Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти:а) уравнение стороны АС; б) длину высоты, проведенной из вершины А; в) величину угла В (в радианах).Решение:а) уравнение стороны АС.Воспользуемся формулой:Уравнение АС:б) длина высоты, проведенной из вершины А.Сначала составим уравнение стороны ВС, к которой проведена высота АН.Длины высоты АН найдем как расстояние от точки А до прямой ВС. Используем формулу:
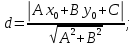
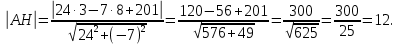
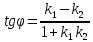
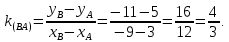
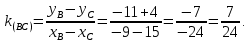
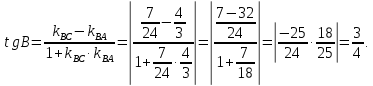
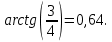
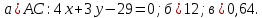
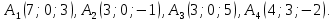
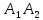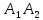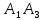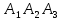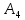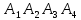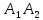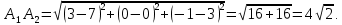
в) величина угла В (в радианах).Для определения угла В воспользуемся формулой тангенса угла между двумя прямыми, имеющими угловые коэффициенты k1 и k2:В нашем случае:Угол В равен Ответ:Задание №2Даны вершины Средствами векторной алгебры найти: а) длину ребра ; б) угол между ребрами и ; в) площадь грани ; г) длину высоты пирамиды, проведенной из вершины ; д) объем пирамиды .Решение:а) Длина .б) угол между ребрам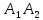и и 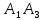.Вычислим координаты векторов: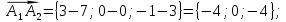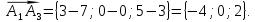Воспользуемся формулой: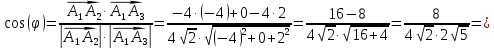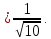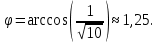в) площадь грани 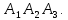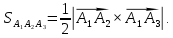Вычислим векторное произведение:
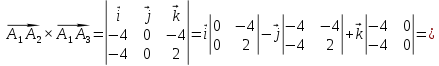
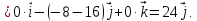
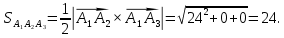
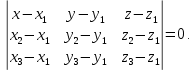
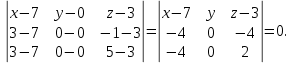
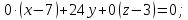
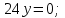
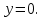
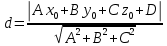
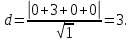
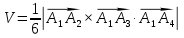
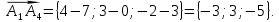
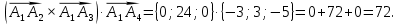
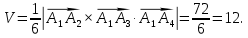
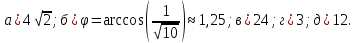
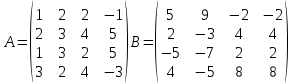
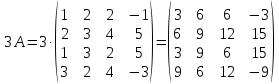
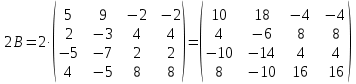
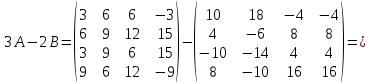
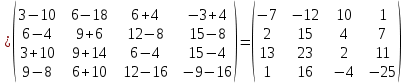
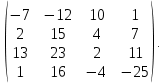
Тогда площадь грани равнаг) длину высоты пирамиды, проведенной из вершины .Составим уравнение плоскости Воспользуемся формулой:Расстояние от точки до плоскости:Длина высоты из вершина А4 равна:д) объем пирамиды .Вычислим смешанное произведение. 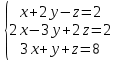Воспользуемся уже найденным векторным произведением:Ответ:Задание №3Найти матрицу C = 3A – 2B, гдеРешение:Ответ: Задание №4Решить систему линейных алгебраических уравнений.Решение:Решим систему методом Гаусса.
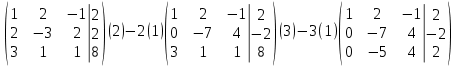
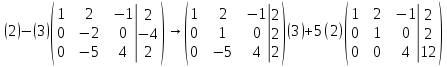
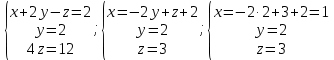
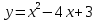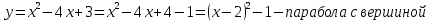
Составим расширенную матрицу и системы и получим нули под главной диагональю.Введем обозначения: (1), (2), (3) – номера строк.Перепишем снова в виде системы и найдем значения x, y, z.Таким образом:x = 1, y = 2, z = 3.Ответ: x = 1, y = 2, z = 3.Задание №5Вычислить площадь фигуры, ограниченной линиями и y = x – 1. 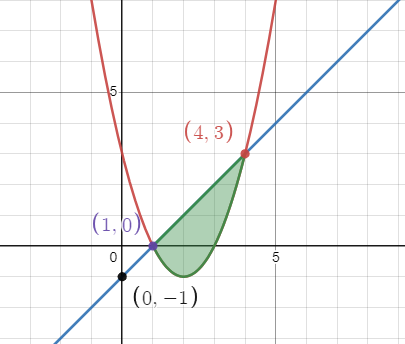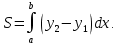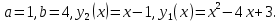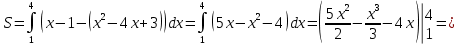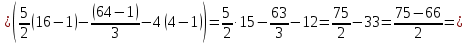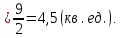Построить график.Решение:Построим линии, ограничивающие фигуру.y = x – 1 – прямая, проходящая через точки (0; -1) и (1; 0).Сделаем чертеж:Вычислим площадь по формуле:Ответ: 4,5 (кв.ед.).Задание №6Оптимальное планирование. Постановка задачи: предприятие располагает ресурсами сырья, рабочей силы и оборудованием, необходимыми для производства любого из трех видов производимых товаров 1, 2, 3. Затраты ресурсов на изготовление единицы данного вида товаров; прибыль, получаемая от реализации единицы товара, а также запасы ресурсов указаны в следующей таблице:

Вид ресурса
Затраты на единицу товара
Запас ресурса

1
2
3

Сырье, кг.
3
5
2
260

Рабочая сила, ч.
22
14
18
400

Оборудование, станко-час.
10
14
8
128

Прибыль, руб.
30
25
56


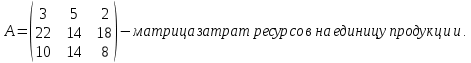
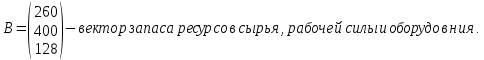
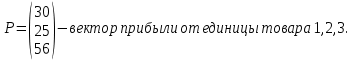
Определить, какой ассортимент товара надо выпускать, чтобы прибыль была максимальной.Решить симплексным методом. Проанализировать полученный результат.Решение:Обозначим х1, х2, х3 – число единиц продукции вида 1, 2 и 3 соответственно, запланированных к производству. Для их изготовления потребуется 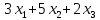кг. сырья, 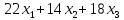ч. рабочей силы, 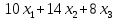станко-час. оборудования. Потребление ресурсов не должно превышать их запасов, соответственно 260, 400 и 128 единиц. 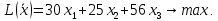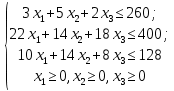Математическая модель задачи имеет вид:Ограничения:Приведем задачу к каноническому виду. 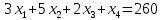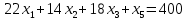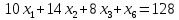Введем дополнительные переменные.Составляем симплексную таблицу 1-ого шага.

ci
БП
30
25
56
0
0
0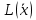


x1
x2
x3
x4
x5
x6
bi

0
x4
3
5
2
1
0
0
260

0
x5
22
14
18
0
1
0
400

0
x6
10
14
8
0
0
1
128



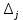-30
-25
-56
0
0
0
0

Смотрите также файлы