Исходное опорное решение:

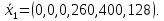
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x₃, так как

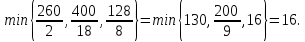
Ключевым элементом является элемент 8 в строке с переменной x6 и в графе с переменной x₃.
Составляем симплексную таблицу 2-ого шага.

ci	БП	30	25	56	0	0	0
		x1	x2	x3	x4	x5	x6	bi
0	x4		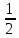	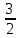0	1	0		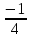228
0	x5		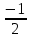	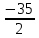0	0	1		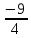112
0	x3		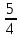	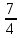1	0	0		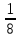16
		896	40	73	0	0	7	0

---

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи, который можно записать так: x₁ = 0, x₂ = 0, x₃ = 16.


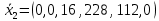
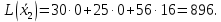
Анализ оптимального плана.
В оптимальный план вошла дополнительная переменная x₄. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 228.

В оптимальный план вошла дополнительная переменная x₅. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 112.

Значение 40 > 0 в столбце x₁ означает, что использование x₁ - не выгодно.

Значение 73 > 0 в столбце x₂ означает, что использование x₂ - не выгодно.

Значение 0 в столбце x₃ означает, что использование x₃ - выгодно.

Ответ:


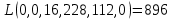
Задание №7
Графический метод. Постановка задачи: для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами 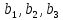соответственно. Расход i-го вида ресурса на изготовление одной единицы j-го вида продукции равен 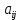, i=1, 2, 3, j=1, 2. Объем выпуска каждого из видов продукции ограничен числом 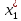и 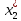единиц, а прибыль, получаемая от реализации одной единицы изготовленной продукции равна c₁ и c₂ соответственно.

Номер ресурса	Объем ресурса (запас)		Номер продукции
			1	2
1	165		3	11
2	58		2	3
3	144		8	1
Ограничения по выпуску		17		14
Прибыль		7		2

---

Требуется составить план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции.
Решение:
Пусть х₁, х₂ – число единиц продукции вида 1 и 2, запланированных к производству.

Для их изготовления потребуется 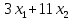единиц ресурса 1, 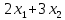единиц ресурса 2, 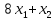единиц ресурса 3.

Составим математическую модель задачи.

Целевая функция будет иметь вид:

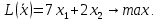
Ограничения задачи:

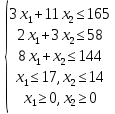
Решим задачу графическим методом. Построим все прямые и отметим область допустимых значений (многоугольник, задающийся неравенствами системы).






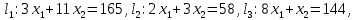
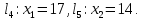
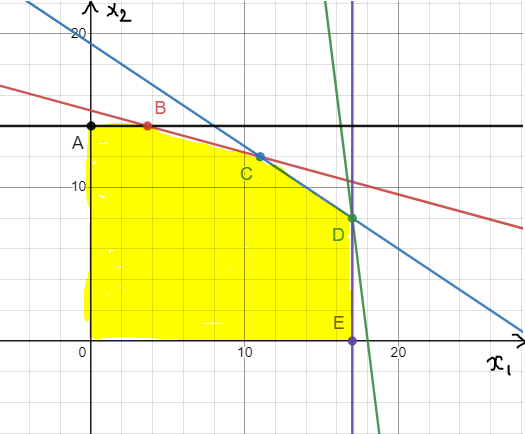
ABCDE – многоугольник решений.
Строим вектор


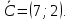
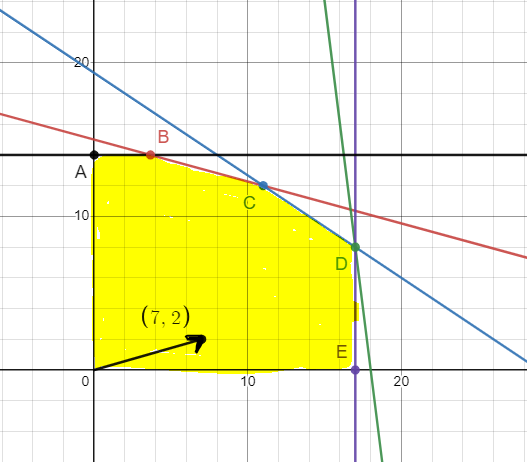
Линия уровня L₀ имеет уравнение
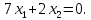
Будем перемещать эту линию вдоль направления вектора 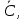пока не достигнем пересечения с самой крайней вершиной многоугольника 9так как нас интересует максимальное значение).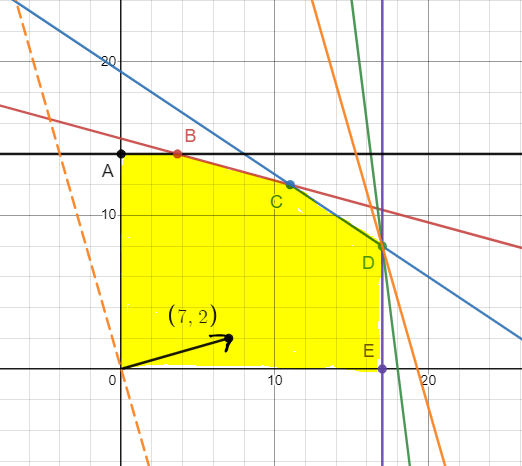


Прямая 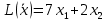достигла пересечения с точкой D. Найдем ее координаты, решив систему: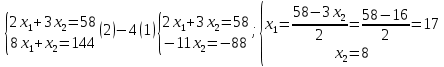

---

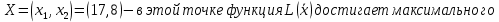
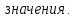
Найдем это значение:


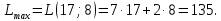
Ответ:


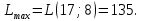
Задание №8
Транспортная задача. Постановка задачи: на складах А₁, А₂, А₃ имеются запасы продукции в количествах 180, 300, 120 т. соответственно. Потребители В₁, В₂, В₃ должны получить эту продукцию в количествах 110, 350, 140 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы матрицей С (ден.ед.)


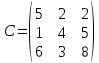
Решение:
Проверим, является ли данная транспортная задача закрытой.




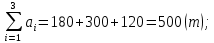
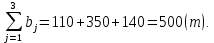
Так как


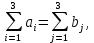
данная транспортная задача закрытая. Найдем исходное опорное по методу минимального тарифа.

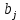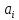		1	2	3
		110	350	140
1	180	5 -	2 180	2 -
2	300	1 110	4 50	5 140
3	120	6 -	3 120	8 -

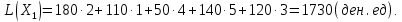
Проверим найденное в этом примере опорное решение на оптимальность, добавив в распределительную таблицу столбец 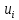и строку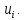

---

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.
u₁ + v₂ = 2; 0 + v₂ = 2; v₂ = 2

u₂ + v₂ = 4; 2 + u₂ = 4; u₂ = 2

u₂ + v₁ = 1; 2 + v₁ = 1; v₁ = -1

u₂ + v₃ = 5; 2 + v₃ = 5; v₃ = 3

u₃ + v₂ = 3; 2 + u₃ = 3; u₃ = 1

		1	2	3
		110	350	140
1	180	5 -	2 180	2 -		0
2	300	1 110	4 50	5 140		2
3	120	6 -	3 120	8 -		1
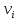		-1	2	3

Рассмотрим клетку (1,3): 3 + 0 > 2, то есть данный план не является оптимальным.
Исходное опорное решение необходимо улучшить.
Выбираем максимальную оценку свободной клетки (1;3): 2. Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

		1	2	3
		110	350	140
1	180	5 -	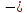2 180	+ 2 -		0
2	300	1 110	+ 4 50	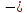5 140		2
3	120	6 -	3 120	8 -		1
		-1	2	3

---

Смотрите также файлы

• Практическая работа 1 Таблица Параметр сравнения фгос ооо фгос соо.docx

• По учебному курсу Теории и технологии начального языкового образования 1 (наименование учебного курса).docx

• Контрольная работа по дисциплине Методы принятия управленческих решений Вариант 5 Институт непрерывного Студент.docx

• Тема моей работы в межаттестационный период.docx

• Лабораторная работа 6 Мишин Александр Проверила Егорова Т. А. Тула 2023.docx