Файл: 1. 1 Кинематический расчет привода.docx

Предварительный расчет

Принимаем, согласно рекомендациям [1c.52], сталь 45:

шестерня: термообработка – улучшение – НВ235÷262 [1c.53],

колесо: термообработка – нормализация – НВ179÷207.

Средняя твердость зубьев:

НВ_1ср = (235+262)/2 = 248

НВ_2ср = (179+207)/2 = 193

Допускаемые контактные напряжения:

[σ]_H = K_HL[σ]_H0,

где K_HL – коэффициент долговечности
K_HL = (N_H0/N)^1/6,

где N_H0 = 1·10⁷ [1c.55],

N = 573ωL_h = 573·9,74·16,5·10³ = 9,21·10⁷.

Так как N > N_H0, то К_HL = 1.

[σ]_H1 = 1,8HB+67 = 1,8·248+67 = 513 МПа.

[σ]_H2 = 1,8HB+67 = 1,8·193+67 = 414 МПа.

[σ]_H = 0,45([σ]_H1 +[σ]_H2) = 0,45(513+414) = 417 МПа.

Допускаемые напряжения изгиба:

[σ]_F = K_FL[σ]_F0,

где K_FL – коэффициент долговечности

Так как N > N_F0 = 4·10⁶, то К_FL = 1.

[σ]_F01 = 1,03HB₁ = 1,03·248 = 255 МПа.

[σ]_F02 = 1,03HB₂ = 1,03·193 = 199 МПа.

[σ]_F1 = 1·255 = 255 МПа.

[σ]_F2 = 1·199 = 199 МПа.

Таблица 2.5 - Механические характеристики материалов зубчатой передачи

Элемент передачи	Марка стали	Dпред	Термоо-бработка	НВср	σв	σ-1	[σ]Н	[σ]F
		Sпред			Н/мм2
Шестерня	45	125/80	Улучш.	248	600	260	513	255
Колесо	45	-	Норм-ия	193	780	335	414	199

Проектировочный расчет

Межосевое расстояние

,

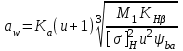где К_а = 43,0 – для косозубых передач [1c.58],

ψ_ba = 0,315 – коэффициент ширины колеса,

К_Нβ = 1,0 – для прирабатывающихся колес.

а_w = 43,0(4,0+1)[309,0·10³·1,0/(417²·4,0²

---

·0,25)]^1/3 = 164,0 мм

принимаем согласно ГОСТ 2185-66 [2 c.52] а_w = 160 мм.

Модуль зацепления

m > 2K_mМ₁/(d₂b₂[σ]_F),

где K_m = 5,8 – для косозубых колес,

d₂ – делительный диаметр колеса,

d₂ = 2a_wu/(u+1) = 2·160·5,0/(5,0 +1) = 267 мм,

b₂ – ширина колеса

b₂ = ψ_baa_w = 0,25·160 = 40 мм.

m > 2·5,8·310,28·10³/267·40·199 = 1,97 мм,

принимаем по ГОСТ 9563-60 m = 2,0 мм.

Основные геометрические размеры передачи



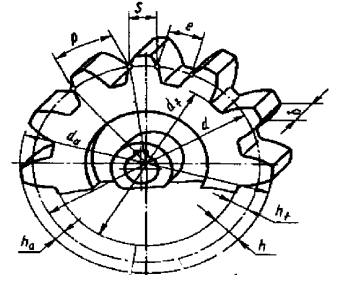
Рисунок 2.1 - Геометрические параметры зубчатого колеса.
Угол наклона зуба

β_min = arcsin(3,5m/b₂) = arcsin(3,5·2/40) = 8,01°

Принимаем β = 8°

Расчет геометрических, кинематических и силовых параметров передачи

При расчетах все линейные и угловые параметры передачи округляем с точностью до третьего знака после запятой.

Суммарное число зубьев:

z_c = 2a_wcosβ/m

z_c = 2·160cos8°/2,0 = 158

Число зубьев шестерни:

z₁ = z_c/(u+1) = 158/(4,0 +1) = 32

Число зубьев колеса:

z₂ = z_c–z₁ = 158 – 32 =126;

уточняем передаточное отношение:

u = z₂/z₁ =126/32 = 3,94,

Отклонение фактического значения от номинального

(3,94 – 4,0)100/4,0 = 1,5% меньше допустимого 3%

Действительное значение угла наклона:

cos = z_cm/2a_W = 1582/2160 = 0,9875   = 9,06°.

Фактическое межосевое расстояние:

a_w = (z₁+z₂)m/2cosβ = (126+32)·2,0/2cos 9,06° = 160 мм.

делительные диаметры

d₁ = mz₁/cosβ = 2,0·32/0,9875= 64,81 мм,

d₂ = 2,0·126/0,9875= 255,19 мм,

диаметры выступов

d_a1 = d₁+2m = 64,81+2·2,0 = 68,81 мм

d_a2 = 255,19+2·2,0 = 259,19 мм

диаметры впадин

d_f1 = d₁ – 2,4m = 68,81 – 2,4·2,0 = 64,01 мм

d_f2 = 259,19 – 2,4·2,0 = 254,39 мм

ширина колеса

b₂ = _baa_w = 0,25·160 = 40 мм

ширина шестерни

b₁ = b₂ + (3÷5) = 40+(3÷5) = 45 мм

Окружная скорость

v = ω₂d₂/2000 = 9,74·255,19/2000 = 1,1 м/с

Принимаем 8-ую степень точности.

Силы действующие в зацеплении

- окружная

F_t = 2М₁/d₁ = 2·229,3·10³/64,81 = 7076 H

- радиальная

F_r = F_ttg/cosβ = 7076tg20º/0,9875= 2575 H

- осевая сила:

F_a = F_ttg = 7076tg 9,06° = 1128 Н.

Проверка межосевого расстояния

а_w = (d₁+d₂)/2 = (64,81+255,19)/2 = 160 мм

Проверка пригодности заготовок

D_заг = d_a1+6 = 64,81+6 = 70,81 мм

Условие D

---

_заг < D_пред = 125 мм выполняется

Для колеса размеры заготовки не лимитируются

Расчетное контактное напряжение

,

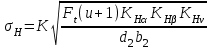где К = 376 – для косозубых колес [1c.64],

К_Нα = 1,06 – для косозубых колес,

К_Нβ = 1,0 – для прирабатывающихся зубьев,

К_Нv = 1,02 – коэффициент динамической нагрузки [1c.65].



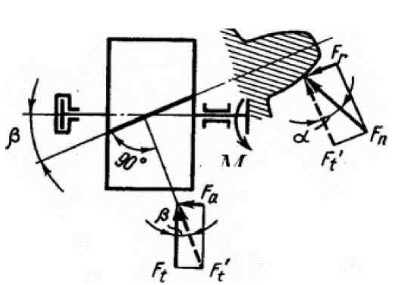
Рисунок 3.2 - Схема сил, действующих в прямозубой цилиндрической передаче
σ_H = 376[7076(4,0+1)1,06·1,0·1,02/(255,19·40)]^1/2 = 406 МПа.

Недогрузка (417 – 406)100/417 = 2,6% допустимо 10%.

Расчетные напряжения изгиба

σ_F2 = Y_F2Y_βF_tK_FαK_FβK_Fv/(mb₂),

где Y_F2 – коэффициент формы зуба,

Y_β = 1 – β/140 = 1 – 9,06/140 = 0,935,

K_Fα = 1,91 – для косозубых колес,

K_Fβ = 1 – для прирабатывающихся зубьев

K_Fv = 1,05 – коэффициент динамической нагрузки [1c.64].

Коэффициент формы зуба:

при z₁ = 32 → z_v1 = z₁/(cosβ)³ = 32/0,9875³ = 33,2 → Y_F1 = 3,85,

при z₂ =126 → z_v2 = z₂/(cosβ)³ =126/0,9875³ = 130,8 → Y_F2 = 3,61.

σ_F2 = 3,61·0,935·7076·1,91·1,0·1,05/2,0·40 = 381,3 МПа < [σ]_F2

σ_F1 = σ_F2Y_F1/Y_F2 = 81,3·3,85/3,61 = 386,6 МПа < [σ]_F1.

Так как расчетные напряжения σ_H < [σ_H] и σ_F < [σ]_F, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях весь срок службы.

Рассчитанные параметры зубчатой передачи заносим в контрольную таблицу 2.6.

Таблица 2.6 Параметры зубчатой передачи

Параметры	Значения
Делительный диаметр колеса; d2,мм	d2=255,19
Диаметры вершин зубьев колес, мм	????????1=68,81, ????????2=259,19
Ширины венцов зубчатых колес; мм	????1=40, ????2=45
Нормальный модуль зубьев колес; ????????, мм	2
Число зубьев колес	????1=32, ????2=126
Угол наклона зубьев колес, ????, градус	9,06
Межосевое расстояние передачи; aw,мм	160
Силы, действующие в зацеплении, Н	????????1=????????2=7076;????????1=????????2=2575;????????1=1128, ????????2=0

---

3. Расчет валов редуктора

Рассчитать ведомый вал одноступенчатого редуктора привода конвейера.

Расположение опор относительно зубчатых колес симметрично. Сила, действующая на вал со стороны цепной передачи F_цen, направлена под углом 0 = 90° к горизонту. Зубчатое колесо вращается по ходу часовой стрелки, если смотреть на него со стороны звездочки. Данные для расчета берем в таблице 1.4 и таблице 3.2 МУ, заносим в таблица 3.1

Таблица 3.1 Исходные данные

Силы в зацеплении, Н			Делительный диаметр колеса; d2,мм	Ширина венца зубчатого колеса, ????2	Вращающий момент на валу колеса, M2, Н∙м
????????2	????????2
7076	2575	1128	255,19	45	1187,0

Все полученные значения параметров, без указаний, округляют до ближайшего большего стандартного числа по ГОСТ 6636-69 (целого четного или кратного 5)

3.1 Проектировочный расчет вала

Выбираем материал вала

Для изготовления вала принимаем сталь 45 с [τ_k] = 20÷30 МПа;. [σ_−1И]= 65 МПа.

Определяем диаметр выходного конца вала из расчета на кручение, d_B, мм:

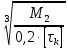dB≥10∙ =10∙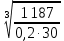 =44,9 (мм)

Округляем значение диаметра до ближайшего большего стандартного: 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 53; 56; 60; 63; 67; 71; 75; 80; 85.

Принемаем Ø45 мм.

Определяем диаметр вала в местах расположения подшипников, dП, мм:

d_П=d_B+2∙t,

где t - высота заплечика подшипника, выбирается из таблицы 4.2 (МУ).

d_П=45+2∙4,0=53,0 (мм),

Расчетное значение округляют до ближайшего большего числа делящегося на «5».

Принимаем Ø55 мм.

Определяем диаметр вала в месте установки зубчатого колеса, dK,мм:

d_K=d_П+3∙r,

где r - координата фаски подшипника, выбирается по таблице 4.2.

d_K=55+3∙3,0=64,0 (мм)

Определяем длину посадочного конца вала под звездочку, l_MT, мм:

l_MT=1,5∙d_B=1,5∙45=67,5 (мм)

Определяем длину промежуточного участка тихоходного вала, l_KT, мм:

l_KT=1,2∙d_П=1,2∙55=66 (мм)

---

Определяем диаметр наружной резьбы конического конца вала, dp, мм:

dp=0,9∙[d_B−0,1l_MT] =0,9∙[45−0,1∙67,5]=34,4 (мм)

Принимаем М36-8g.

Примечание: Входной и выходной валы редукторов имеют цилиндрические или конические консольные участки для установки полумуфт, шкивов, звездочек, зубчатых колес. Размеры консольных участков стандартизированы: ГОСТ 12080-66 «Концы валов цилиндрические»; ГОСТ12081-72 «Концы валов конические».



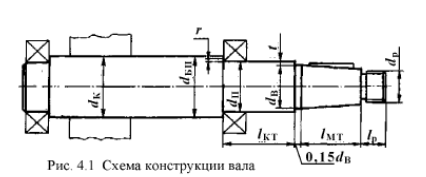
Рисунок 4.1 - Схема конструкции вала.
Конструктивно назначаем: l1, l2, l3:

l2=l3=b2⁄2+(20…30)= 45/2+(20…30)=60 (мм),

l1=44+(10…20)= 60 (мм)

Проверочный расчет вала

Горизонтальная плоскость.

Сумма моментов сил и реакций опор относительно опоры А

m_A = 60F_t – 120B_X + 62F_вг = 0

Отсюда находим реакцию опоры В в плоскости XOZ

B_X = (7076·60+228·62)/120 = 1035 H

Сумма моментов сил и реакций опор относительно опоры В

m_В = 60F_t – 120А_X –182F_вг = 0

Отсюда находим реакцию опоры А в плоскости XOZ

А_X = (2575·60 – 228·182)/120 = 571 H

Изгибающие моменты в плоскости XOZ

M_X1 =1128·60 = 62,1 Н·м

M_X1 = 228·62 = 14,1 Н·м

Проверка

А_Х – F_t +B_X + F_вг = 571 – 1834 +1035+228 = 0

Вертикальная плоскость.

Сумма моментов сил и реакций опор относительно опоры А

Быстроходный вал

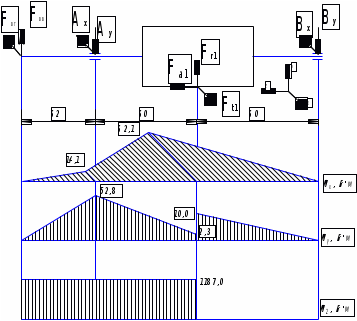
Рисусок 4.2 – Схема нагружения быстроходного вала
m_A = 60F_r + 120B_Y – F_a1d₁/2 – 62F_вв = 0

Отсюда находим реакцию опор В в плоскости YOZ

B_Y = (-676·60 +292·52,66/2 + 852·62)/120 =166 H

Сумма моментов сил и реакций опор относительно опоры B

m_A = 60F_r – 120A_Y + F_a1d₁/2 + 182F_вв = 0

Отсюда находим реакцию опор A в плоскости YOZ

A_Y = (676·60 +292·52,66/2 + 852·182)/124 = 1694 H

Проверка

F_вв + B_Y + F_r – A_Y = 852+166+676 – 1694 = 0

Изгибающие моменты в плоскости YOZ

M_Y =166·60 =10,0 Н·м

M_Y = 852·62 = 52,8 Н·м

M_Y = 852·122 – 1694·60 = 2,3 Н·м

Суммарные реакции опор:

А = (А_Х² + А_Y²)^0,5 = (571² +1694²)^0,5 =1788 H

B= (B_Х² + B_Y²)^0,5 = (1035² +166²)^0,5 =1048 H

Тихоходный вал


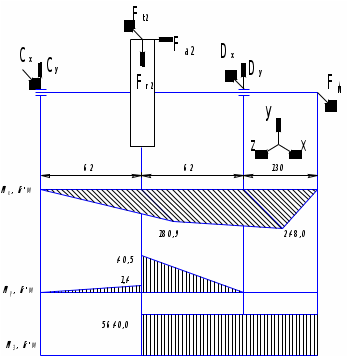
Рисунок 4.3 – Схема нагружения тихоходного вала.

---