Файл: Контрольная работа по дисциплине Логистика нефтегазоснабжения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 99
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, определяется по формуле
где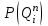 – вероятность того, что на склад прибудет
– вероятность того, что на склад прибудет  грузов;
грузов; 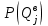 – вероятность того, что со склада будет выдано
– вероятность того, что со склада будет выдано 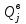 грузов.
грузов.
В качестве исходных данных для определения расчетной величины складских запасов грузов задаются распределения величин прибытия и выдачи грузов (за сутки, за смену или за час):
где ,
, 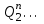 ,
,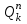 – возможные значения суточных грузопотоков прибытия (k – число этих значений);
– возможные значения суточных грузопотоков прибытия (k – число этих значений);  ,
, 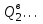 ,
, 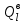 – возможные значения суточных грузопотоков выдачи груза со склада (l – число этих значений);
– возможные значения суточных грузопотоков выдачи груза со склада (l – число этих значений);
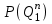 ,
, 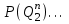 ,
, 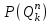 – вероятности появления соответствующих величин суточного прибытия грузов;
– вероятности появления соответствующих величин суточного прибытия грузов; 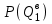 ,
, 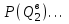 ,
, 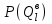 – вероятности появления соответствующих величин суточного грузопотока выдачи грузов со склада.
– вероятности появления соответствующих величин суточного грузопотока выдачи грузов со склада.
Величина страхового запаса грузов принимается равной разности максимальной величины выдачи
принимается равной разности максимальной величины выдачи 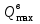 и минимальной величины приема грузов
и минимальной величины приема грузов 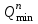 из заданных распределений этих величин:
из заданных распределений этих величин: 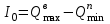
(для снабжающих складов) и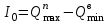 (для складов готовой продукции и других перевалочных складов) или может задаваться в виде некоторого нормативного неснижаемого запаса (в особых случаях):
(для складов готовой продукции и других перевалочных складов) или может задаваться в виде некоторого нормативного неснижаемого запаса (в особых случаях): 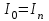 .
.
Доверительную вероятность (надежность оценки) определения расчетной величины складских запасов грузов рекомендуется принимать
[Р] = 0,950. Это равносильно условию, что вместимость склада может оказаться недостаточной только в 5 % случаев (или 13–18 дней за год).
Задача. Пусть нужно определить расчетный запас хранения грузов для склада со следующими распределениями прибытия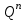 и выдачи грузов
и выдачи грузов 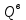 :
:
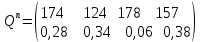 ;
;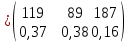 ,
,
где 174, 124, 178, 157 и 119, 89, 187 – количество поддонов с грузом, соответственно принимаемых и выдаваемых со склада за сутки; 0,28; 0,34; 0,06; 0,38 и 0,37; 0,38; 0,16 – соответствующие вероятности прибытия и выдачи таких количеств грузов.
Решение:
Определяем страховой запас:
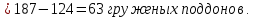
Доверительную вероятность (надежность оценки) определения расчетной величины складских запасов грузов принимаем [Р] = 0,93.
1-е сочетание грузопотоков: запас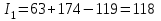 , вероятность такого запаса
, вероятность такого запаса 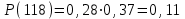 ;
;
2-е сочетание грузопотоков: запас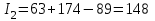 , вероятность такого запаса
, вероятность такого запаса 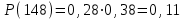 ;
;
3-е сочетание грузопотоков: запас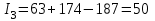 , вероятность такого запаса
, вероятность такого запаса 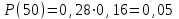 ;
;
4-е сочетание грузопотоков: запас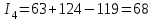 , вероятность такого запаса
, вероятность такого запаса 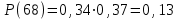 ;
;
5-е сочетание грузопотоков: запас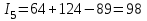
, вероятность такого запаса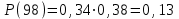 ;
;
6-е сочетание грузопотоков: запас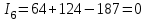 , вероятность такого запаса
, вероятность такого запаса 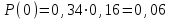 .
.
7-е сочетание грузопотоков: запас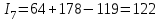 , вероятность такого запаса
, вероятность такого запаса 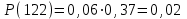 ;
;
8-е сочетание грузопотоков: запас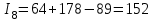 , вероятность такого запаса
, вероятность такого запаса 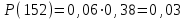 ;
;
9-е сочетание грузопотоков: запас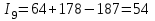 , вероятность такого запаса
, вероятность такого запаса 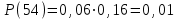 ;
;
10-е сочетание грузопотоков: запас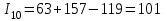 , вероятность такого запаса
, вероятность такого запаса 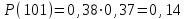 ;
;
11-е сочетание грузопотоков: запас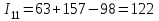 , вероятность такого запаса
, вероятность такого запаса 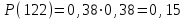 ;
;
12-е сочетание грузопотоков: запас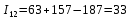 , вероятность такого запаса
, вероятность такого запаса 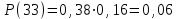 .
.
Проверяем нормировочное условие, по которому сумма вероятностей всех событий, образующих полную группу, должна быть равна единице:
Нормировочное условие выполняется.
Получим следующее распределение запасов грузов на складе
Определяем интегральную функцию распределения (накопленную вероятность) от меньших величин запасов к большим:
Из этой функции видно, что заданная доверительная вероятность складских запасов [Р] = 0,93 попадает в последний интервал накопленных вероятностей: 0,86 < [Р] = 0,93 < 1,00.
Поэтому расчетную величину складских запасов ищем в интервале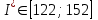 , определяя ее по формуле линейной интерполяции:
, определяя ее по формуле линейной интерполяции:
Таким образом, при заданных закономерностях прибытия и отправления грузов склад должен быть рассчитан на единовременное хранение 137 транспортных пакетов с грузом.
Вывод:
В данной работе по заданным исходным данным, используя метод определения складских запасов грузов, разработанный д-ром техн. наук О.Б. Маликовым, определили расчетный запас хранения грузов для склада со следующими распределениями прибытия и выдачи грузов которая у нас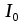 составило 63 груженых поддонов. Исходя из страхового запаса нашли 12 сочетаний грузопотоков и проверили нормировочные условия по которому сумма вероятностей всех событий образующих полную группу составляет единицу. Убедившись, что нормативное условие выполняется, получили следующие распределения запасов груза на складе и по этим распределением запасов грузов определили интегральную функцию от меньших величин запасов к большим. Из этой функции видно что заданная вероятность складских запасов [Р] = 0,93 попадает в предпоследний интервал накопленных вероятностей . Исходя из расчетной величины складских запасов нашли примерный интеграл где
составило 63 груженых поддонов. Исходя из страхового запаса нашли 12 сочетаний грузопотоков и проверили нормировочные условия по которому сумма вероятностей всех событий образующих полную группу составляет единицу. Убедившись, что нормативное условие выполняется, получили следующие распределения запасов груза на складе и по этим распределением запасов грузов определили интегральную функцию от меньших величин запасов к большим. Из этой функции видно что заданная вероятность складских запасов [Р] = 0,93 попадает в предпоследний интервал накопленных вероятностей . Исходя из расчетной величины складских запасов нашли примерный интеграл где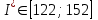 и определили вместимость склада на основании нормативных сроков хранения грузов которая составило у меня 137 транспортных пакетов с грузом.
и определили вместимость склада на основании нормативных сроков хранения грузов которая составило у меня 137 транспортных пакетов с грузом.
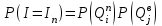 ,
, 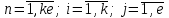 , (2.2)
, (2.2)
где
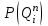 – вероятность того, что на склад прибудет
– вероятность того, что на склад прибудет  грузов;
грузов; 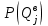 – вероятность того, что со склада будет выдано
– вероятность того, что со склада будет выдано 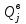 грузов.
грузов.В качестве исходных данных для определения расчетной величины складских запасов грузов задаются распределения величин прибытия и выдачи грузов (за сутки, за смену или за час):
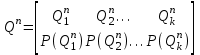 , (2.3)
, (2.3)
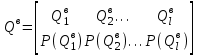 , (2.4)
, (2.4)
где
 ,
, 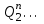 ,
,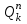 – возможные значения суточных грузопотоков прибытия (k – число этих значений);
– возможные значения суточных грузопотоков прибытия (k – число этих значений);  ,
, 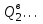 ,
, 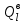 – возможные значения суточных грузопотоков выдачи груза со склада (l – число этих значений);
– возможные значения суточных грузопотоков выдачи груза со склада (l – число этих значений); 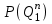 ,
, 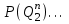 ,
, 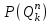 – вероятности появления соответствующих величин суточного прибытия грузов;
– вероятности появления соответствующих величин суточного прибытия грузов; 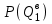 ,
, 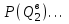 ,
, 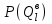 – вероятности появления соответствующих величин суточного грузопотока выдачи грузов со склада.
– вероятности появления соответствующих величин суточного грузопотока выдачи грузов со склада.Величина страхового запаса грузов
 принимается равной разности максимальной величины выдачи
принимается равной разности максимальной величины выдачи 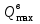 и минимальной величины приема грузов
и минимальной величины приема грузов 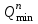 из заданных распределений этих величин:
из заданных распределений этих величин: 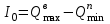
(для снабжающих складов) и
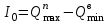 (для складов готовой продукции и других перевалочных складов) или может задаваться в виде некоторого нормативного неснижаемого запаса (в особых случаях):
(для складов готовой продукции и других перевалочных складов) или может задаваться в виде некоторого нормативного неснижаемого запаса (в особых случаях): 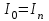 .
.Доверительную вероятность (надежность оценки) определения расчетной величины складских запасов грузов рекомендуется принимать
[Р] = 0,950. Это равносильно условию, что вместимость склада может оказаться недостаточной только в 5 % случаев (или 13–18 дней за год).
Задача. Пусть нужно определить расчетный запас хранения грузов для склада со следующими распределениями прибытия
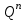 и выдачи грузов
и выдачи грузов 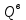 :
: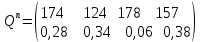 ;
;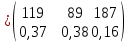 ,
,где 174, 124, 178, 157 и 119, 89, 187 – количество поддонов с грузом, соответственно принимаемых и выдаваемых со склада за сутки; 0,28; 0,34; 0,06; 0,38 и 0,37; 0,38; 0,16 – соответствующие вероятности прибытия и выдачи таких количеств грузов.
Решение:
Определяем страховой запас:
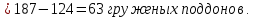
Доверительную вероятность (надежность оценки) определения расчетной величины складских запасов грузов принимаем [Р] = 0,93.
1-е сочетание грузопотоков: запас
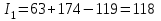 , вероятность такого запаса
, вероятность такого запаса 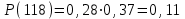 ;
;2-е сочетание грузопотоков: запас
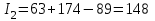 , вероятность такого запаса
, вероятность такого запаса 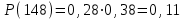 ;
;3-е сочетание грузопотоков: запас
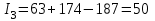 , вероятность такого запаса
, вероятность такого запаса 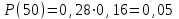 ;
;4-е сочетание грузопотоков: запас
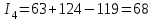 , вероятность такого запаса
, вероятность такого запаса 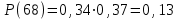 ;
;5-е сочетание грузопотоков: запас
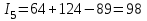
, вероятность такого запаса
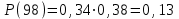 ;
;6-е сочетание грузопотоков: запас
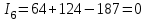 , вероятность такого запаса
, вероятность такого запаса 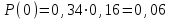 .
.7-е сочетание грузопотоков: запас
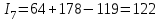 , вероятность такого запаса
, вероятность такого запаса 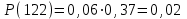 ;
;8-е сочетание грузопотоков: запас
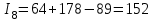 , вероятность такого запаса
, вероятность такого запаса 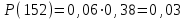 ;
;9-е сочетание грузопотоков: запас
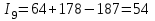 , вероятность такого запаса
, вероятность такого запаса 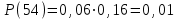 ;
;10-е сочетание грузопотоков: запас
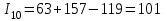 , вероятность такого запаса
, вероятность такого запаса 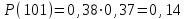 ;
;11-е сочетание грузопотоков: запас
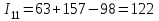 , вероятность такого запаса
, вероятность такого запаса 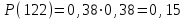 ;
;12-е сочетание грузопотоков: запас
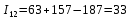 , вероятность такого запаса
, вероятность такого запаса 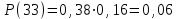 .
.Проверяем нормировочное условие, по которому сумма вероятностей всех событий, образующих полную группу, должна быть равна единице:
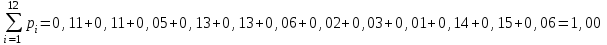 .
.
Нормировочное условие выполняется.
Получим следующее распределение запасов грузов на складе
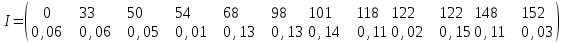 .
.
Определяем интегральную функцию распределения (накопленную вероятность) от меньших величин запасов к большим:
| I | 0 | 33 | 50 | 54 | 68 | 98 | 101 | 118 | 122 | 122 | 148 | 152 |
| Ф(I) | 0,06 | 0,12 | 0,17 | 0,18 | 0,31 | 0,44 | 0,58 | 0,69 | 0,71 | 0,86 | 0,97 | 1,00 |
Из этой функции видно, что заданная доверительная вероятность складских запасов [Р] = 0,93 попадает в последний интервал накопленных вероятностей: 0,86 < [Р] = 0,93 < 1,00.
Поэтому расчетную величину складских запасов ищем в интервале
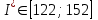 , определяя ее по формуле линейной интерполяции:
, определяя ее по формуле линейной интерполяции: 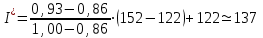 .
.
Таким образом, при заданных закономерностях прибытия и отправления грузов склад должен быть рассчитан на единовременное хранение 137 транспортных пакетов с грузом.
Вывод:
В данной работе по заданным исходным данным, используя метод определения складских запасов грузов, разработанный д-ром техн. наук О.Б. Маликовым, определили расчетный запас хранения грузов для склада со следующими распределениями прибытия и выдачи грузов которая у нас
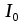 составило 63 груженых поддонов. Исходя из страхового запаса нашли 12 сочетаний грузопотоков и проверили нормировочные условия по которому сумма вероятностей всех событий образующих полную группу составляет единицу. Убедившись, что нормативное условие выполняется, получили следующие распределения запасов груза на складе и по этим распределением запасов грузов определили интегральную функцию от меньших величин запасов к большим. Из этой функции видно что заданная вероятность складских запасов [Р] = 0,93 попадает в предпоследний интервал накопленных вероятностей . Исходя из расчетной величины складских запасов нашли примерный интеграл где
составило 63 груженых поддонов. Исходя из страхового запаса нашли 12 сочетаний грузопотоков и проверили нормировочные условия по которому сумма вероятностей всех событий образующих полную группу составляет единицу. Убедившись, что нормативное условие выполняется, получили следующие распределения запасов груза на складе и по этим распределением запасов грузов определили интегральную функцию от меньших величин запасов к большим. Из этой функции видно что заданная вероятность складских запасов [Р] = 0,93 попадает в предпоследний интервал накопленных вероятностей . Исходя из расчетной величины складских запасов нашли примерный интеграл где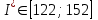 и определили вместимость склада на основании нормативных сроков хранения грузов которая составило у меня 137 транспортных пакетов с грузом.
и определили вместимость склада на основании нормативных сроков хранения грузов которая составило у меня 137 транспортных пакетов с грузом.