В статье рассмотрены числовые равенства с целыми, положительными, взаимно простыми основаниями и натуральным показателем степени n > 1. Найдены условия верности таких числовых равенств. Показано, что такие числовые равенства существуют при показателе степени равном количеству слагаемых равенства, а знаменитая большая теорема Ферма является частным случаем приведенной теоремы. Поскольку теорема доказана на довольно простом уровне, то это является доказательством того, что Ферма не ошибся и действительно доказал свою знаменитую теорему.
О показателе степени некоторых числовых равенств
Соловьев Анатолий Борисович, бывший инженер-технолог Санкт-Петербургского института ядерной физики, ныне пенсионер.

198218 г. Санкт-Петербург, ул. Дмитриевская (Володарский), д. 2, корп. 2.

Майл: anatolii1000000@mail.ru
Реферат. В предлагаемой работе рассмотрены числовые равенства вида:



Установлено, что в подобных верных числовых равенствах с натуральным показателем степени n > 1 и целых, взаимно простых (не имеющих никаких общих множителей кроме 1) положительных основаниях степеней , входящих в него слагаемых и суммы , показатель степени n равен количеству слагаемых R этого равенства.

Ключевые слова: числовые равенства, теорема Ферма.
Теорема: Верное числовое равенство вида:

(1)

где: , – целые, положительные, взаимно простые основания степеней

слагаемых и суммы

---

;

n > 1 – натуральный показатель степени,

существует при n = R, где: R – количество слагаемых в числовом равенстве.
Доказательство:

Пусть существуют удовлетворяющие условиям теоремы основания степеней , для которых числовое равенство (1) верно. Представим каждое из входящих в числовое равенство слагаемое и сумму в виде тождеств, являющихся биномами Ньютона при натуральном показателе степени n:



(2)

где: Хк, У – могут принимать любые значения, то есть, являются переменными.

Подставляя тождества (2) в числовое равенство (1), получим алгебраическое уравнение:

(3)

Поменяв местами символы сумм, и вынеся коэффициенты за символ суммы независящий от значений n и i, что равнозначно перестановке мест слагаемых в уравнении (3), получим:

(4)

Алгебраическое уравнение (4) соответствует числовому равенству (1) и справедливо при любых значениях переменных Хк, У, входящих в это уравнение.
Лемма.

Если существует верное числовое равенство (1), где:

, – целые, положительные, основания степеней слагаемых и

суммы ,

n > 1 – натуральный показатель степени,

то в соответствующем ему алгебраическом уравнении (4) для любого значения переменной У можно найти такие значения переменных Хк, при которых будут равны между собой все соответствующие слагаемые обеих частей этого равенства.
Доказательство леммы:

---

Пусть существует удовлетворяющее условиям леммы верное числовое равенство (1), а следовательно и соответствующее ему алгебраическое уравнение (4).

Пусть утверждение леммы верно и в алгебраическом уравнении (4) можно найти такие переменные Хк, У, для которых выполняется система уравнений, состоящая из (n + 1) уравнения:





(5)

……………………………………………



Следует отметить, что система уравнений (5) существует для числового равенства (1) только в том случае, если основания , являются целыми числами. Если, например, число иррациональное (при этом число является числом целым по условию), то при показателе степени n > 1 можно подобрать целые переменные Хк, У такими, что все левые части системы уравнений (5) будут целыми, в то время как в правой части часть уравнений будет иметь иррациональные значения, что является противоречием.

Аналогично система уравнений (5) может не существовать и для числовых равенств типа (1) если основаниями степеней являются рациональные дроби.
Пусть основания , целые, положительные числа. Для таких числовых равенств существует система уравнений (5). Система уравнений при помощи тождественных преобразований приводится к виду (преобразование системы уравнений приведено в приложении 1):

---

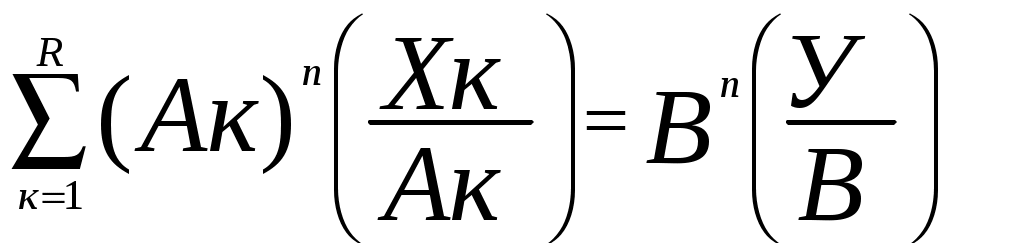
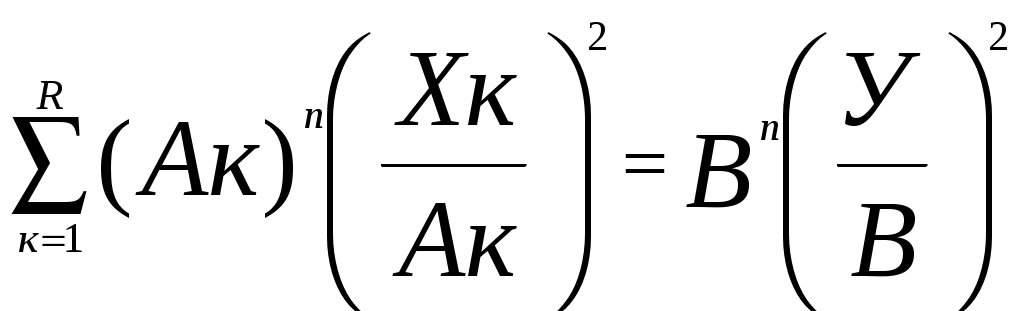(6)

……………………………



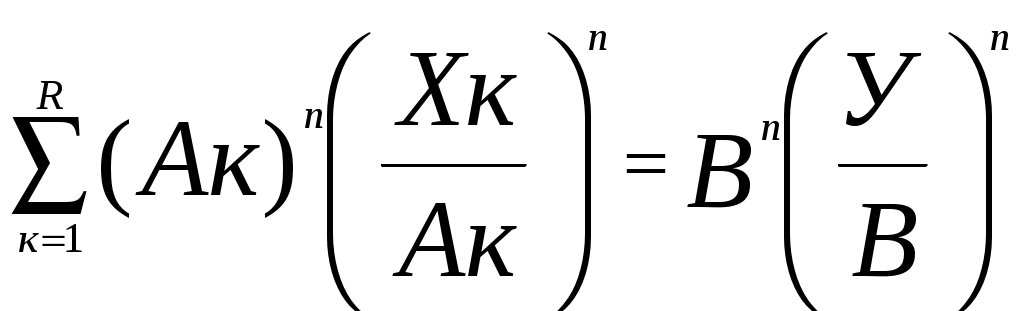
Следовательно, если существуют удовлетворяющие условиям леммы основания степеней , для которых числовое равенство (1) верное, то существуют соответствующая ему система уравнений (5) и преобразованная система уравнений (6).

По условию показатель степени n входящих в равенство слагаемых и суммы больше 1. Тогда количество уравнений в системе уравнений (6) не меньше 3.

Умножая первое уравнение полученной системы на множитель (У/В)², а второе на (-2У/В), и складывая первые три равенства, получим:

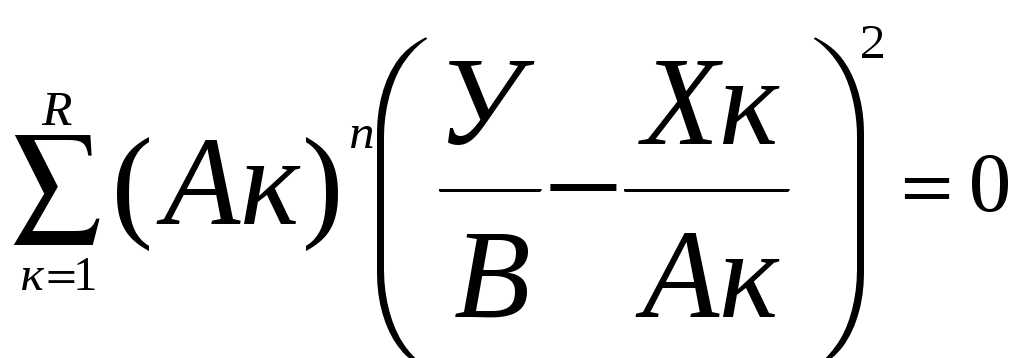(7)

Следовательно, если существуют такие целые основания степеней и , для которых числовое равенство (1) верно при n > 1, то существует соответствующее этому числовому равенству алгебраическое уравнение (7).

По условию леммы основания , , а следовательно и слагаемые , являются положительными числами. Тогда для выполнения равенства (7), (поскольку квадрат множителя в скобках при любых значениях входящих в него переменных не отрицателен), необходимо выполнение условий:

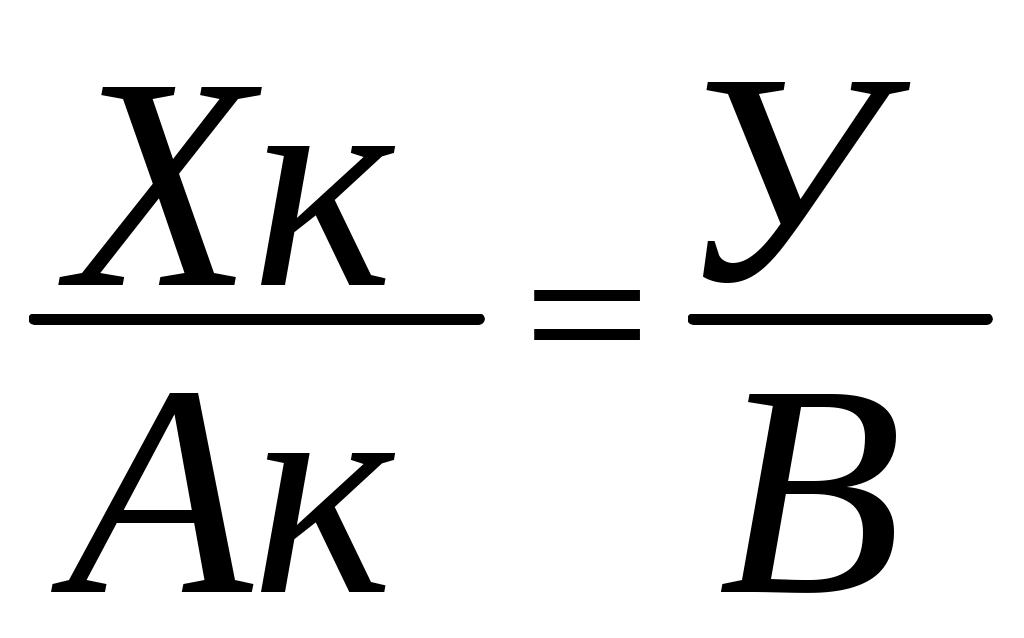(8)

где индекс к пробегает значения от 1 до R (R – количество слагаемых в числовом равенстве (1)).

Или в виде системы уравнений:

---

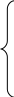
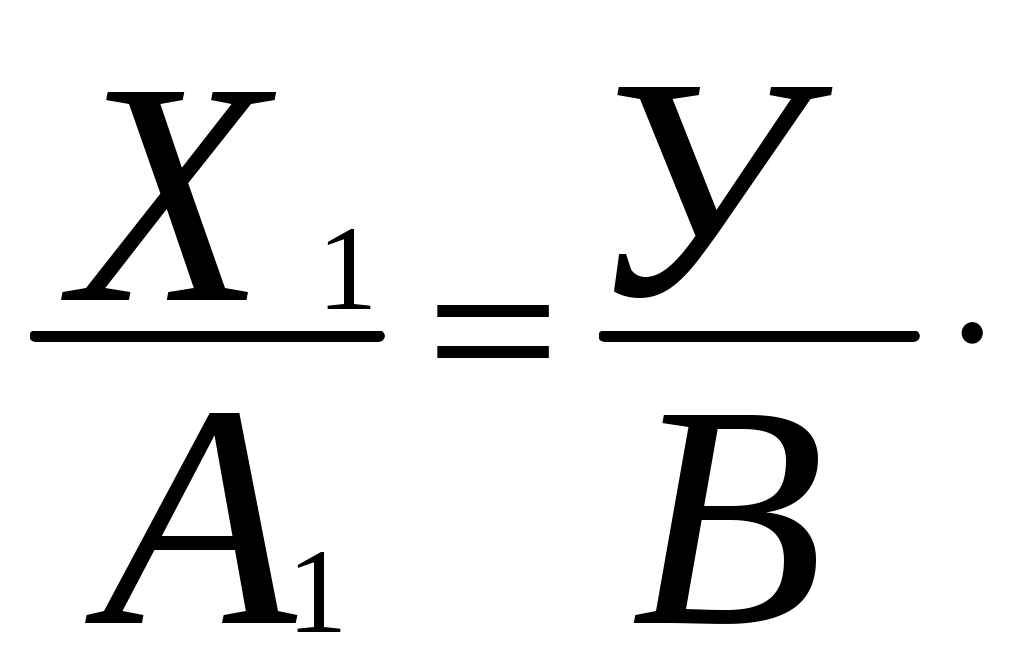
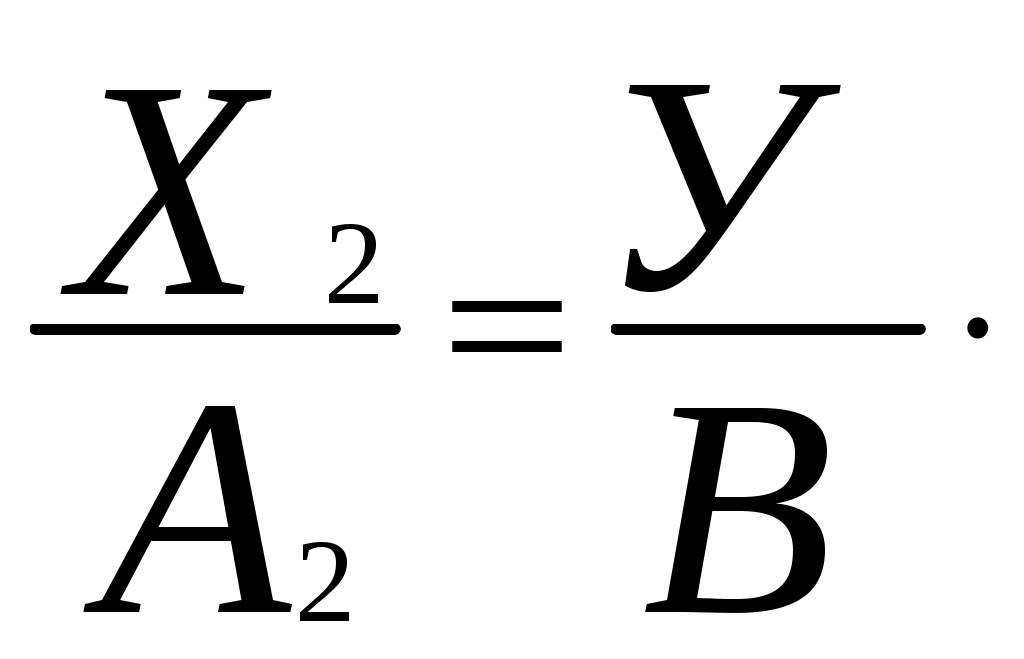(9)

……………



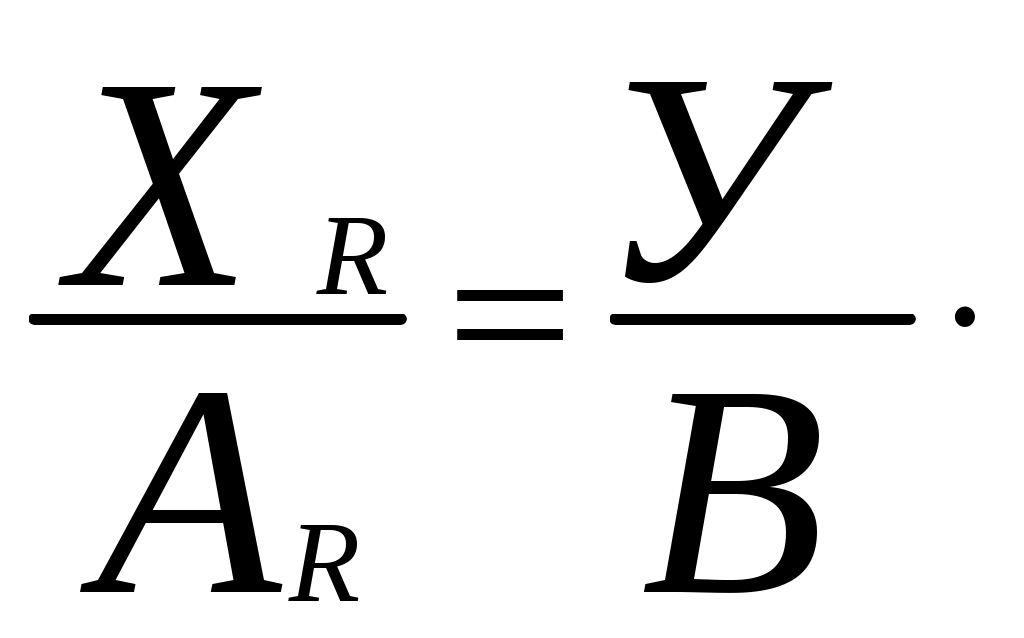
Полученные условия преобразования (9) содержат R уравнений (где R – количество слагаемых равенства (1)) и устанавливают при заданных целых, положительных основаниях , соотношения между переменными уравнения (4), при которых любому значению одной из переменных У или Хк можно найти такие значения остальных переменных, при которых будут равны между собой все соответствующие слагаемые обеих частей уравнения (4) (в этом можно убедиться, подставив полученные соотношения (9) в равенство (4)).

Таким образом, если числовое равенство (1) верное, положительные основания степеней и слагаемых и суммы являются целыми числами, а натуральный показатель степени n  1, то существует соответствующее ему тождественно преобразованное алгебраическое уравнение (4) и условия его преобразования (9), позволяющие преобразовать одну часть уравнения (4) к виду его другой части. Условия преобразования (9) из всей совокупности верных и неверных числовых равенств типа (1) при показателе степени n  1 выделяют верные числовые равенства и, если эти условия не выполняются, то не существует и верного числового равенства (1).

Очевидно, что уравнения, входящие в систему уравнений (9), имеют нетривиальные (отличные от ноля) решения (все уравнения системы являются линейными, а одной из переменных можно задавать любое значение).

Следовательно, верное числовое равенство типа (1) при выполнении условий леммы можно преобразовать к виду (4), где каждое из слагаемых правой части будет равно сумме соответствующих слагаемых левой части.

Лемма доказана.
Полученная система уравнений (9) имеет однозначные решения только в том случае

---

Смотрите также файлы

• Зеленого цвета характеризует гибкость волевых проявлений в сложных условиях деятельности, чем обеспечивается поддержание работоспособности, а выбор серого цвета.docx

• Факторы эмоциональных состояний в интимноличностных отношениях.pdf

• Некоммерческое акционерное общество.pdf

• Контрольная работа по дисциплине Правоохранительные и судебные органы.docx

• Задание Изучите раздел 1, составьте перечень основных объектов бухгалтерского учета, дайте их определения. На основе полученных результатов составьте сводную таблицу объектов бухгалтерского учета.docx