Файл: Реферат. В предлагаемой работе рассмотрены числовые равенства вида.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, если хотя бы одно из оснований слагаемых или суммы не может быть представлено в виде другого целого основания с некоторым натуральным показателем степени отличным от 1.
Если все основания числового равенства (1) можно представить в виде некоторых целых положительных чисел с отличным от 1 натуральным показателем степени, то, выбрав какое либо из уравнений системы (9) (для примера взято первое уравнение), будем иметь:
Откуда получаем для нового основания в:
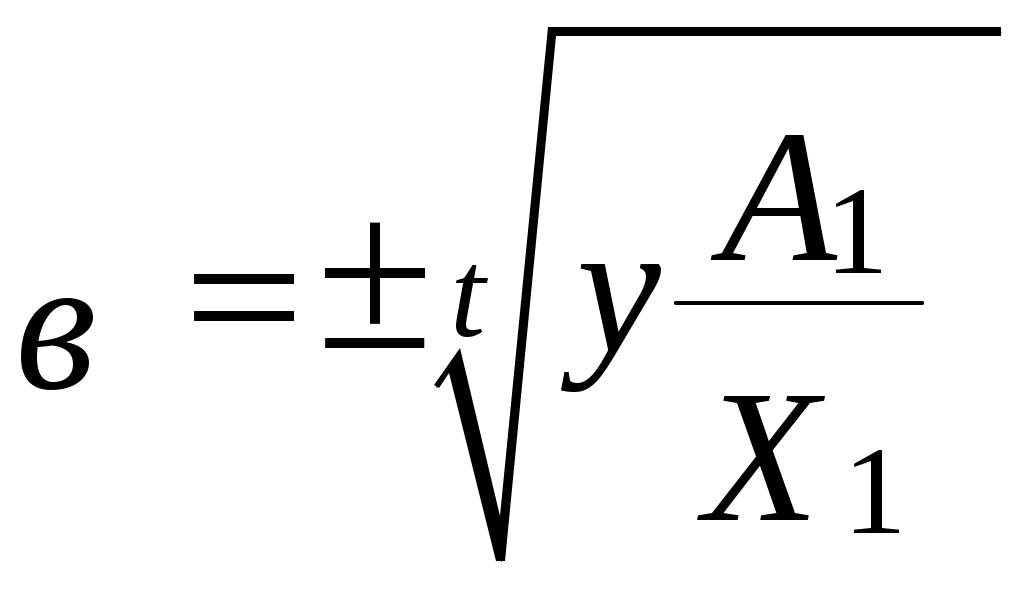
Полученное значение основания в имеет как положительные, так и отрицательные значения (их количество равно t), что противоречит условию теоремы. По условию теоремы оно должно иметь положительное значение.
Если все основания числового равенства можно представить в виде некоторых целых чисел с отличным от 1 показателем степени, то это говорит о неверности выбора показателя степени всего числового равенства (1). В этом случае в системе уравнений (9) решения каждого уравнения будут иметь неоднозначные, отличающиеся знаком, значения, противоречащие исходному числовому равенству.
Только если показатель степени t хотя бы одного из входящих в числовое равенство оснований равен 1, то все уравнения системы (9) становятся однозначными (Они путем перестановок приводятся к виду, когда в каждом уравнении будет однозначное значение основания в).
Числовые равенства типа (1), удовлетворяющие условиям теоремы, удовлетворяют и условиям леммы. Для таких равенств существует тождественно преобразованное алгебраическое уравнение (4) и соответствующие ему условия преобразования (9) определяющие его верность. Следовательно, для удовлетворяющих условиям теоремы верных числовых равенств типа (1), существует система уравнений:
……………
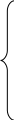
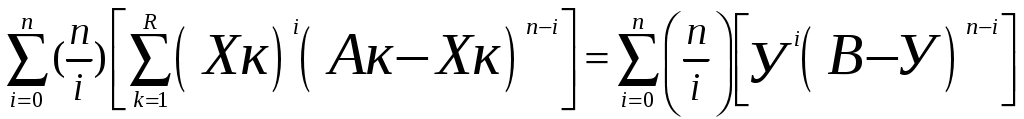
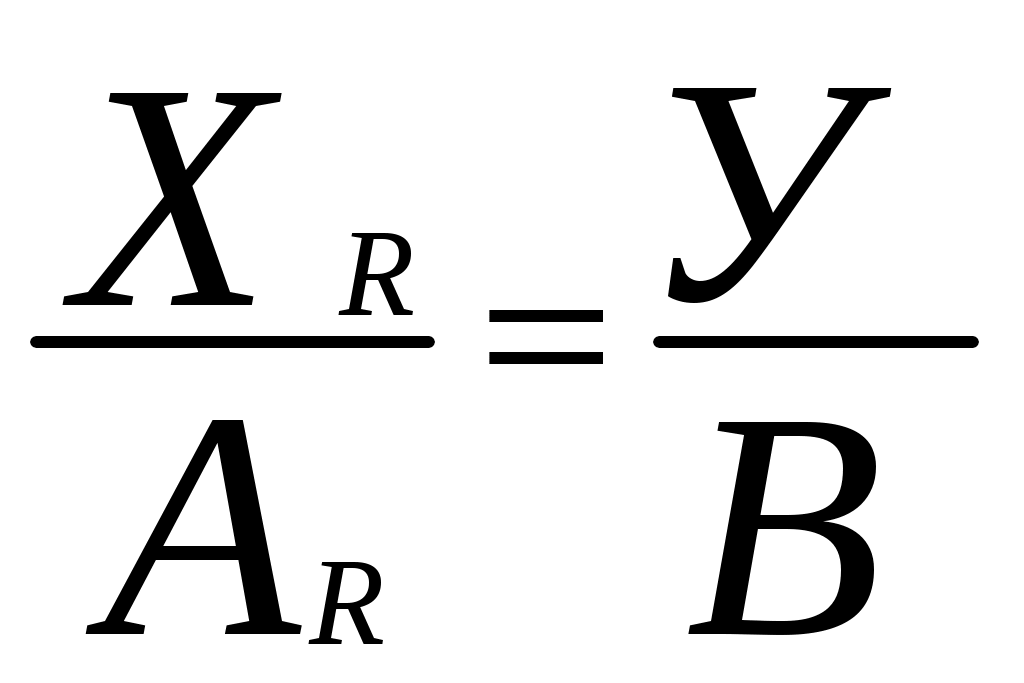
Или, что тоже самое:
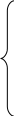
(10)
……………
По условию теоремы все основания степеней
, 
являются взаимно простыми числами, а следовательно в системе уравнений (10) нет сократимых и одинаковых уравнений при любой их перестановке.
Полученная система уравнений приводится к виду системы уравнений (6):
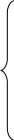
(11)
…………………………………
Она отличается от системы уравнений (6) только количеством уравнений в системе. В системе уравнений (6) количество уравнений равно (n + 1), а в системе уравнений (11) оно равно (R + 1), где R – количество слагаемых числового равенства (1).
Система уравнений (11) очевидно является равносильной системе уравнений (6) (системы уравнений имеют одни и те же решения и относятся к одному и тому же числовому равенству).
Система уравнений (11) при помощи тождественных преобразований аналогичных преобразованиям приложения № 1, но в обратном порядке (свертка системы уравнений (11)), приводится к равенству типа (1) только в том случае, если показатель степени n = R (где R – количество слагаемых в равенстве (1)).
Следовательно, если существует удовлетворяющее условиям теоремы верное числовое равенство типа (1) с показателем степени n 1, то его показатель степени n = R, что и требовалось доказать.
Теорема нарушается, если среди оснований , имеются сократимые числа.
Чтобы показать это, предположим, что существует числовое равенство:
в котором основания степени
и 
являются сократимыми. Запишем их в виде:
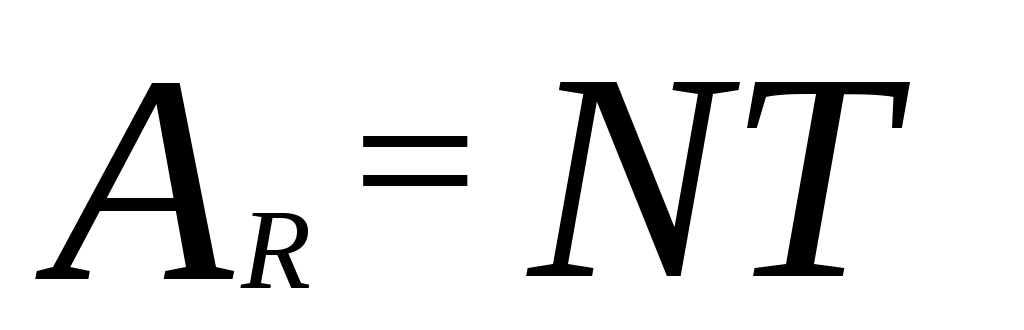
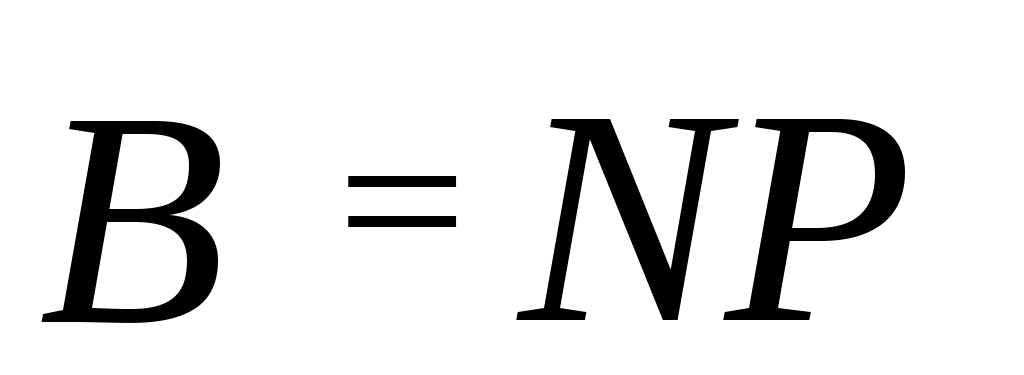
где: P и T – целые, несократимые числа, N – общий множитель.
Тогда числовое равенство примет вид:
(12)
После проведения операций 3 – 8 получим для условий преобразования систему уравнений аналогичную системе уравнений (9):
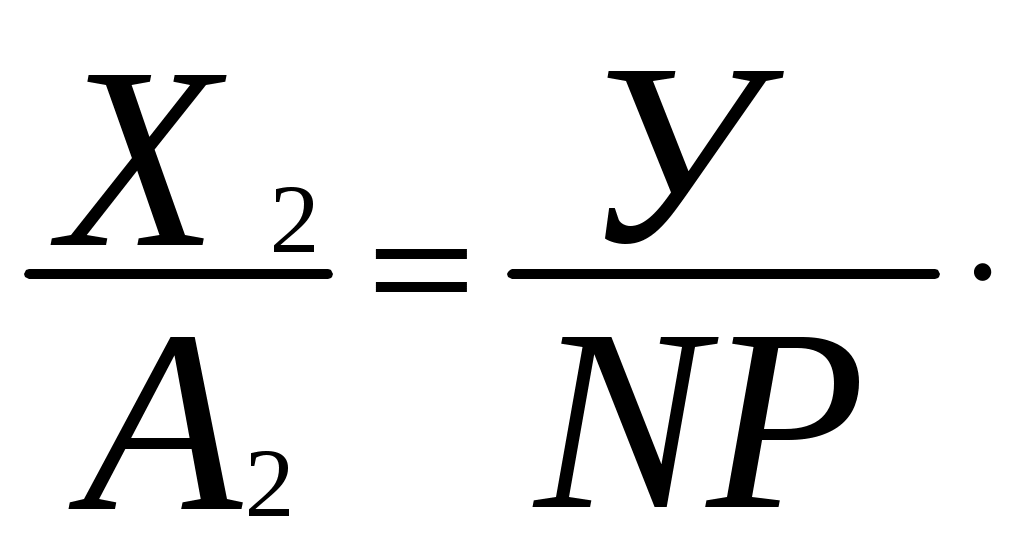(13)
……………
А соответствующая числовому равенству система уравнений (аналогичная системе уравнений (10)) примет вид:
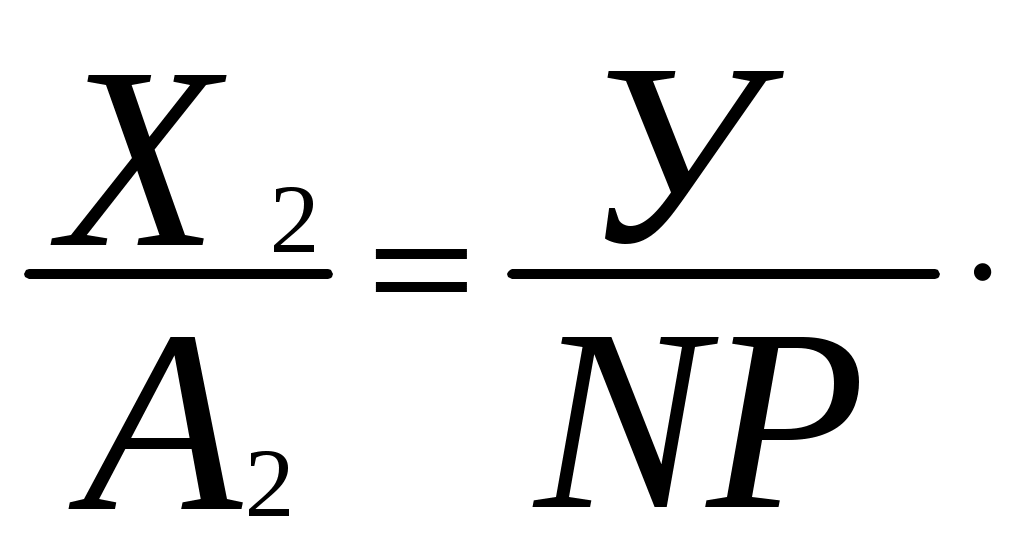(14)
……………
Последнее уравнение в полученной системе уравнений является сократимым, что и приведет к нарушению теоремы.
Свертка системы уравнений (14) соответствует числовому равенству (12), а свертка этой же системы уравнений после сокращения последнего уравнения невозможна без умножения на множитель (последнее уравнение относится к иному числовому равенству). Для исключения этой неоднозначности необходимо рассматривать подобные исходные числовые равенства (12) первоначально разделив их на множитель N:
(15)
Полученное числовое равенство (15) содержит в своем составе как целые основания степеней, так и рациональные дроби, что выходит за рамки теоремы (нарушается требование целостности оснований числового равенства (1)), может привести к нарушению леммы (невозможности представления в виде системы уравнений (5) аналогично наличию среди оснований иррациональных чисел) и соответственно нарушению теоремы.
Выводы из теоремы:
Согласно теореме числовые равенства типа (1), удовлетворяющие условиям теоремы, имеют показатель степени n = R (где: R - количество слагаемых в равенстве). Теорема может быть нарушена если среди оснований , имеются сократимые числа.
Исключение составляют числовые равенства имеющие в своем составе только два слагаемых. Такие числовые равенства при отсутствии иррациональных оснований всегда приводимы к условиям теоремы (доказательство приведено в приложении 2).
Следовательно, натуральный показатель степени числовых равенств типа (1) при отсутствии иррациональных оснований и количестве слагаемых R = 2 не может быть больше 2 (большая теорема Ферма).
P.S.: Приведенная выше теорема является частью более общей теоремы. Аналогично можно доказать, что верное числовое равенство вида:
где: Ак, Вt – целые, положительные, взаимно простые, основания степеней слагаемых (Ак)n и суммы (Вt)n;
n > 1 – натуральный показатель степени,
существует при n = (R + N – 1), где: R и N – количество слагаемых соответственно в левой и правой частях равенства.
Доказательство ничем не отличается от приведенного выше, за исключением применения необходимого количества операций аналогичной операции перехода из системы уравнений (6) к уравнению (7) (эта операция позволяет поочередно исключать слагаемые из одной части равенства) и далее получения условий аналогичных условию (8).
Приложение 1.
Пусть имеем систему уравнений (5):
……………………………………………….
Вынеся множители
и 
за скобки, преобразуем ее к виду:
……………………………………………………..
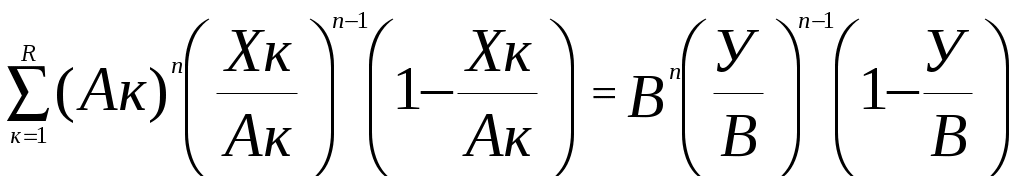
Каждое уравнение системы является комбинацией всех предшествующих ему в этой системе уравнений. Для исключения из какого либо i-го уравнения системы всех предшествующих ему уравнений этой же системы, необходимо предшествующие ему уравнения до i-го включительно умножить на коэффициенты бинома Ньютона соответствующие показателю степени i и произвести свертку полученных таким образом уравнений. Тогда, после свертки этих уравнений для i-го уравнения системы получим:
Или окончательно i-ое уравнение системы будет иметь вид:
Проделав аналогичные операции по разделению уравнений с каждым из уравнений системы, получим систему уравнений аналогичную системе уравнений (6):
…………………………………………
Если все основания числового равенства (1) можно представить в виде некоторых целых положительных чисел с отличным от 1 натуральным показателем степени, то, выбрав какое либо из уравнений системы (9) (для примера взято первое уравнение), будем иметь:
Откуда получаем для нового основания в:
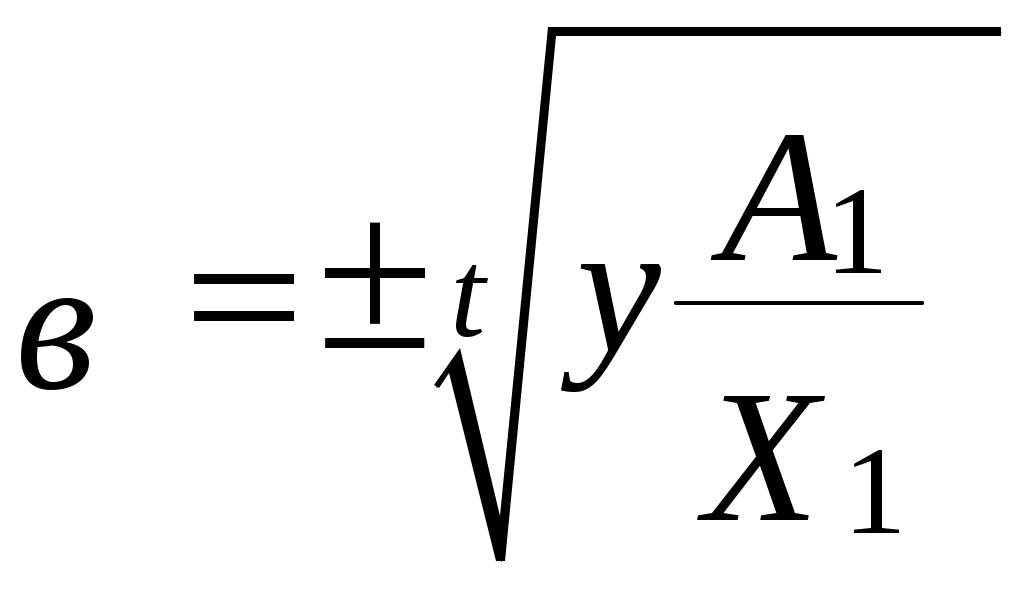
Полученное значение основания в имеет как положительные, так и отрицательные значения (их количество равно t), что противоречит условию теоремы. По условию теоремы оно должно иметь положительное значение.
Если все основания числового равенства можно представить в виде некоторых целых чисел с отличным от 1 показателем степени, то это говорит о неверности выбора показателя степени всего числового равенства (1). В этом случае в системе уравнений (9) решения каждого уравнения будут иметь неоднозначные, отличающиеся знаком, значения, противоречащие исходному числовому равенству.
Только если показатель степени t хотя бы одного из входящих в числовое равенство оснований равен 1, то все уравнения системы (9) становятся однозначными (Они путем перестановок приводятся к виду, когда в каждом уравнении будет однозначное значение основания в).
Числовые равенства типа (1), удовлетворяющие условиям теоремы, удовлетворяют и условиям леммы. Для таких равенств существует тождественно преобразованное алгебраическое уравнение (4) и соответствующие ему условия преобразования (9) определяющие его верность. Следовательно, для удовлетворяющих условиям теоремы верных числовых равенств типа (1), существует система уравнений:
……………
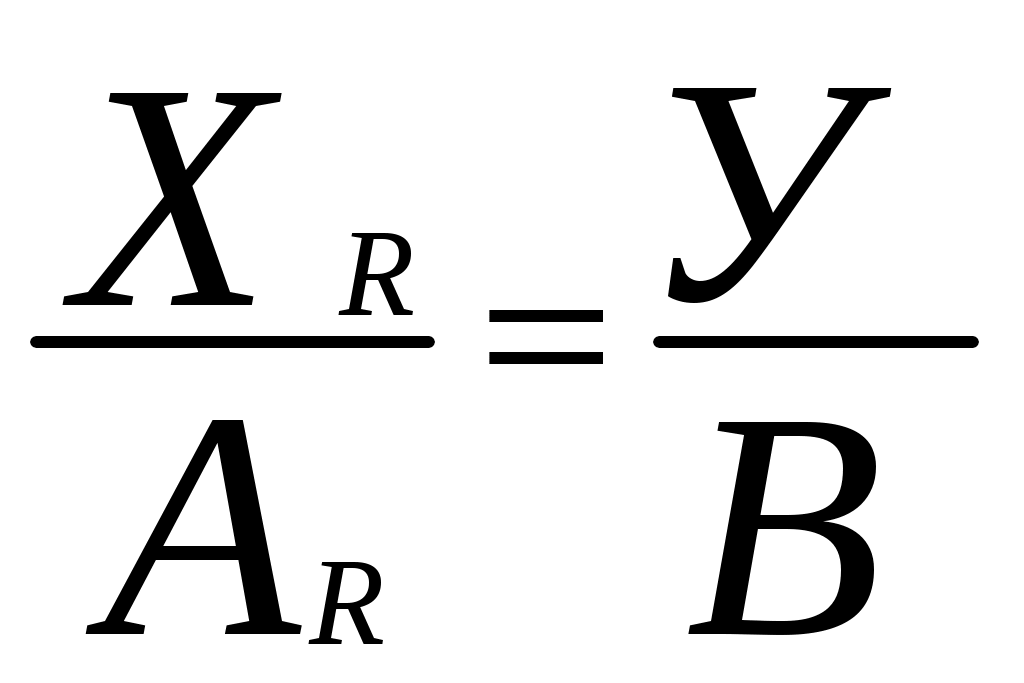
Или, что тоже самое:
(10)……………
По условию теоремы все основания степеней
, являются взаимно простыми числами, а следовательно в системе уравнений (10) нет сократимых и одинаковых уравнений при любой их перестановке.Полученная система уравнений приводится к виду системы уравнений (6):
(11)…………………………………
Она отличается от системы уравнений (6) только количеством уравнений в системе. В системе уравнений (6) количество уравнений равно (n + 1), а в системе уравнений (11) оно равно (R + 1), где R – количество слагаемых числового равенства (1).
Система уравнений (11) очевидно является равносильной системе уравнений (6) (системы уравнений имеют одни и те же решения и относятся к одному и тому же числовому равенству).
Система уравнений (11) при помощи тождественных преобразований аналогичных преобразованиям приложения № 1, но в обратном порядке (свертка системы уравнений (11)), приводится к равенству типа (1) только в том случае, если показатель степени n = R (где R – количество слагаемых в равенстве (1)).
Следовательно, если существует удовлетворяющее условиям теоремы верное числовое равенство типа (1) с показателем степени n 1, то его показатель степени n = R, что и требовалось доказать.
Теорема нарушается, если среди оснований
, имеются сократимые числа.
Чтобы показать это, предположим, что существует числовое равенство:
в котором основания степени
и являются сократимыми. Запишем их в виде: где: P и T – целые, несократимые числа, N – общий множитель.
Тогда числовое равенство примет вид:
(12)После проведения операций 3 – 8 получим для условий преобразования систему уравнений аналогичную системе уравнений (9):
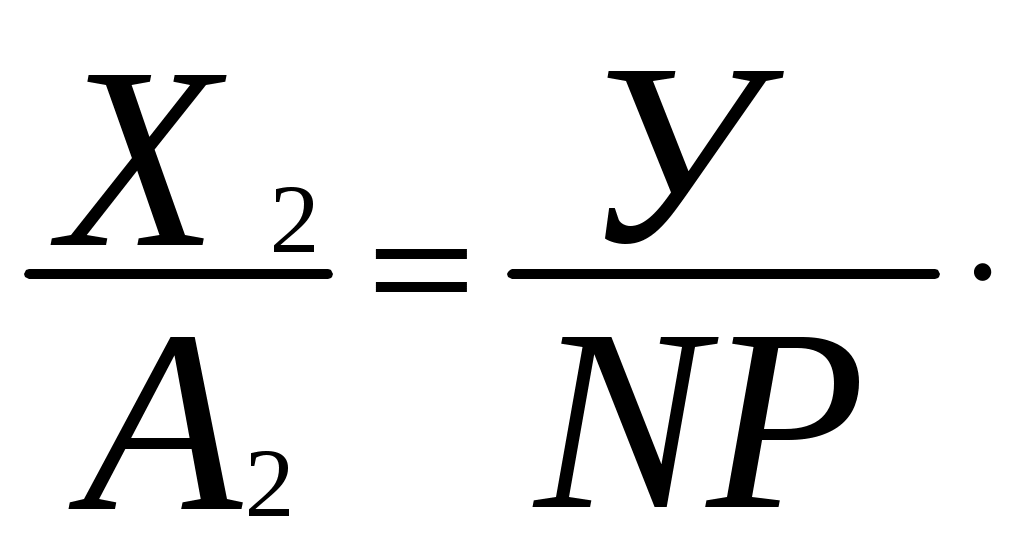(13) ……………
А соответствующая числовому равенству система уравнений (аналогичная системе уравнений (10)) примет вид:
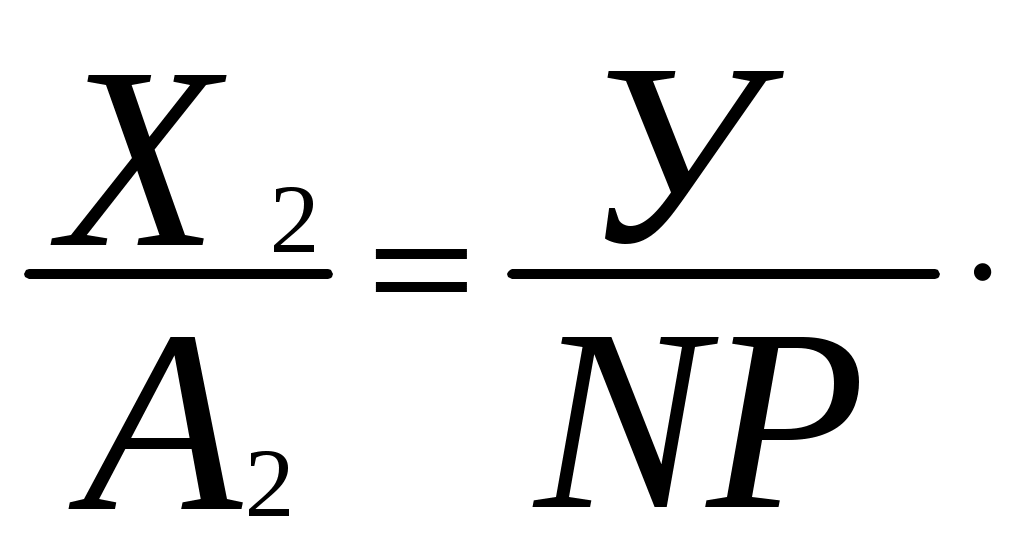(14) ……………
Последнее уравнение в полученной системе уравнений является сократимым, что и приведет к нарушению теоремы.
Свертка системы уравнений (14) соответствует числовому равенству (12), а свертка этой же системы уравнений после сокращения последнего уравнения невозможна без умножения на множитель (последнее уравнение относится к иному числовому равенству). Для исключения этой неоднозначности необходимо рассматривать подобные исходные числовые равенства (12) первоначально разделив их на множитель N:
(15)Полученное числовое равенство (15) содержит в своем составе как целые основания степеней, так и рациональные дроби, что выходит за рамки теоремы (нарушается требование целостности оснований числового равенства (1)), может привести к нарушению леммы (невозможности представления в виде системы уравнений (5) аналогично наличию среди оснований иррациональных чисел) и соответственно нарушению теоремы.
Выводы из теоремы:
Согласно теореме числовые равенства типа (1), удовлетворяющие условиям теоремы, имеют показатель степени n = R (где: R - количество слагаемых в равенстве). Теорема может быть нарушена если среди оснований
, имеются сократимые числа.Исключение составляют числовые равенства имеющие в своем составе только два слагаемых. Такие числовые равенства при отсутствии иррациональных оснований всегда приводимы к условиям теоремы (доказательство приведено в приложении 2).
Следовательно, натуральный показатель степени числовых равенств типа (1) при отсутствии иррациональных оснований и количестве слагаемых R = 2 не может быть больше 2 (большая теорема Ферма).
P.S.: Приведенная выше теорема является частью более общей теоремы. Аналогично можно доказать, что верное числовое равенство вида:
где: Ак, Вt – целые, положительные, взаимно простые, основания степеней слагаемых (Ак)n и суммы (Вt)n;
n > 1 – натуральный показатель степени,
существует при n = (R + N – 1), где: R и N – количество слагаемых соответственно в левой и правой частях равенства.
Доказательство ничем не отличается от приведенного выше, за исключением применения необходимого количества операций аналогичной операции перехода из системы уравнений (6) к уравнению (7) (эта операция позволяет поочередно исключать слагаемые из одной части равенства) и далее получения условий аналогичных условию (8).
Приложение 1.
Пусть имеем систему уравнений (5):
……………………………………………….
Вынеся множители
и за скобки, преобразуем ее к виду: ……………………………………………………..
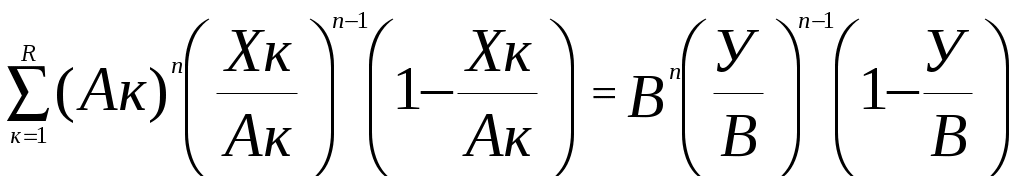
Каждое уравнение системы является комбинацией всех предшествующих ему в этой системе уравнений. Для исключения из какого либо i-го уравнения системы всех предшествующих ему уравнений этой же системы, необходимо предшествующие ему уравнения до i-го включительно умножить на коэффициенты бинома Ньютона соответствующие показателю степени i и произвести свертку полученных таким образом уравнений. Тогда, после свертки этих уравнений для i-го уравнения системы получим:
Или окончательно i-ое уравнение системы будет иметь вид:
Проделав аналогичные операции по разделению уравнений с каждым из уравнений системы, получим систему уравнений аналогичную системе уравнений (6):
…………………………………………