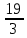Добавлен: 25.10.2023
Просмотров: 43
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Раздел № 1. Линейная алгебра
Задача 1, вариант 6
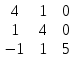
φА (λ) = [A-λЕ]
φА (λ) =
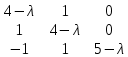
(4-λ)*(4-λ)*(5-λ) + (-1)*1*0 + 1*1*0 – (-1)*(4-λ)*0 – (4- λ)*1*0 – 1*1*(5- λ) =
(4- λ)2*(5-λ) – (5- λ) = (16 – 8λ + λ2)* (5- λ) – (5- λ) = 80 - 16λ - 40λ + 8λ2 + 5λ2 – λ3 – 5 + λ = 75 - 55λ + 13λ2 – λ3
φА (λ) = – λ3 + 13λ2 - 55λ – 75
φА (λ) = 0
– λ3 + 13λ2 - 55λ – 75 = 0
(5 – λ)*((4- λ)2 -1) = 0
5 – λ = 0 (4- λ)2 - 1= 0
λ1 = 5 16 - 8λ + λ2 – 1 = 0
λ2 - 8λ + 15 = 0
Найдем корни квадратного уравнения через дискриминант
d = b2 – 4ac
d = (-8)2 – 4*1*15 = 64 – 60 = 4
λ2 =
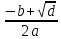 =
= 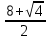 = 5
= 5λ3=
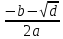 =
= 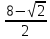 = 3
= 3Таким образом, матрица имеет имеет два собственных значения λ1 = 5 и λ2 = 3.
Находим собственные векторы заданной матрицы:
Aν = λν, ν ≠ 0
А=
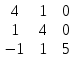 ν1 =
ν1 = 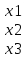 λ1 = 5
λ1 = 5 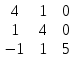 *
* 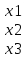 = 5 *
= 5 * 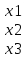
Получаем и решаем следующую систему:
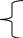 4х1 + х2 = 5х1
4х1 + х2 = 5х1х1 + 4х2 = 5х2
-х1 + х2 + 5х3 = 5х3
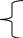 4х1 + х2 - 5х1 = 0
4х1 + х2 - 5х1 = 0х1 + 4х2 - 5х2 = 0
-х1 + х2 + 5х3 - 5х3 = 0
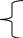 -х1 + х2 = 0
-х1 + х2 = 0х1 – х2 = 0
-х1 + х2 = 0
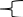 х1 – х2 = 0
х1 – х2 = 0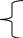
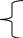
х1 = х2 х2
х2 = х2 , х = х2
х3 = х3 х3
Пусть х2 = 1, х3 = 0, тогда собственный вектор заданной матрицы ν1 =
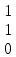
Пусть х2 = 0, х3 = 1, тогда собственный вектор заданной матрицы ν2 =
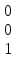
А=
 ν2 =
ν2 =  λ2 = 3
λ2 = 3Получаем и решаем следующую систему:
 4х1 + х2 = 3х1
4х1 + х2 = 3х1х1 + 4х2 = 3х2
-х1 + х2 + 5х3 = 3х3
 4х1 + х2 - 3х1 = 0
4х1 + х2 - 3х1 = 0х1 + 4х2 - 3х2 = 0
-х1 + х2 + 5х3 - 3х3 = 0
 х1 + х2 = 0
х1 + х2 = 0х1 + х2 = 0
-х1 + х2 + 2х3 = 0
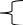 х1 + х2 = 0
х1 + х2 = 0-х1 + х2 + 2х3 = 0
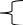 х1 + х2 = 0
х1 + х2 = 0х2 + х2 + 2х3 = 0
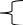 х1 + х2 = 0
х1 + х2 = 02х2 + 2х3 = 0
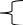 х1 + х2 = 0
х1 + х2 = 0х2 + х3 = 0
х

 1 = х1 х1
1 = х1 х1х2 = -х1 , х = -х1
х3 = х1 х1
Пусть х1 = 1, тогда собственный вектор заданной матрицы ν3 =
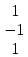
Раздел № 1. Линейная алгебра
Задача 2, вариант 8
По теореме Кронера-Капелли система алгебраических уравнений совместима тогда и только тогда, когда ранг матрицы системы А равен рангу раширенной системы Ã, т.е. rang A = rang Ã.
Составим матрицу и расширенную матрицу системы
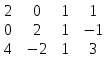
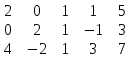
Т.к. размер полученных матриц 3х4 и 3х5, значит ранг обеих матриц не больше 3, т.е. rang A
< 3, rang à < 3.
Найдем ранг первой матрицы:
 1 строку делим на 2
1 строку делим на 2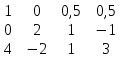 от 3 строки отнимаем 1 строку, умноженную на 4
от 3 строки отнимаем 1 строку, умноженную на 4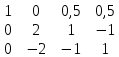 2 строку делим на 2
2 строку делим на 2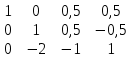 к 3 строке прибавляем 2 строку, умноженную на 2
к 3 строке прибавляем 2 строку, умноженную на 2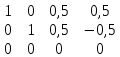 , т.к. ненулевых строк 2, то rang A = 2
, т.к. ненулевых строк 2, то rang A = 2Найдем ранг расширенной матрицы:
 1 строку делим на 2
1 строку делим на 2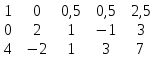 от 3 строки отнимаем 1 строку, умноженную на 4
от 3 строки отнимаем 1 строку, умноженную на 4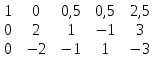 2 строку делим на 2
2 строку делим на 2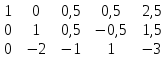 к 3 строке прибавляем 2 строку, умноженную на 2
к 3 строке прибавляем 2 строку, умноженную на 2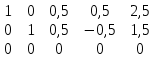 , т.к. ненулевых строк 2, то rang à = 2
, т.к. ненулевых строк 2, то rang à = 2Так как rang A = rang Ã, то согласно теореме Кронера-Капелли заданная система алгебраических уравнений совместима. Так как ранги обеих систем меньше 4 (числа неизвестных), данная система имеет бесконечное количество решений.
Решение заданной системы уравнений методом Крамера и средствами матричного исчисления невозможно, т.к. матрица из данной системы не является квадратной (количество уравнений не равно числу неизвестных).
 Решим заданную систему методом Гаусса:
Решим заданную систему методом Гаусса:2

 х1 + х3 + х4 = 5
х1 + х3 + х4 = 52х2 + х3 – х4 = 3 1 строку умножаем на 2 и вычитаем из строки 3
4х1 – 2х2 + х3 + 3х4 = 7
2х1 + х3 + х4 = 5
2х2 + х3 – х4 = 3
4х1 – 2х2 + х3 + 3х4 – 4х1 – 2х3 – 2х4= 7 – 10
2х1 + х3 + х4 = 5
2х2 + х3 – х4 = 3 2 строку вычитаем из строки 3
– 2х2 – х3 + х4 =-3
2

х1 + х3 + х4 = 5
2х2 + х3 – х4 = 3
– 2х2 – х3 + х4 +2х2 + х3 – х4 = -3+ 3
2х1 + х3 + х4 = 5
2х2 + х3 – х4 = 3
Из уравнения первой подсистемы найдем х1:
х1 = 2,5 – 0,5х3 – 0,5х4
Из уравнения второй подсистемы найдем х2:
х2 = 1,5 – 0,5х3 + 0,5х4
Ответ: х1 = 2,5 – 0,5х3 – 0,5х4
х2 = 1,5 – 0,5х3 + 0,5х4
х3 = х3
х4 = х4
Раздел № 1. Линейная алгебра
Задача 3, вариант 3
По теореме Кронера-Капелли система алгебраических уравнений совместима тогда и только тогда, когда ранг матрицы системы А равен рангу раширенной системы Ã, т.е. rang A = rang Ã.
Составим матрицу и и найдем ее ранг:
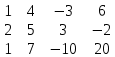 из 2 строки вычитаем 1 строку, умноженную на 2
из 2 строки вычитаем 1 строку, умноженную на 2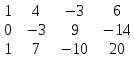 из 3 строки вычитаем 1 строку
из 3 строки вычитаем 1 строку 2 строку делим на -3
2 строку делим на -3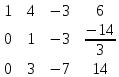 из 3 строки вычитаем 2 строку, умноженную на 3
из 3 строки вычитаем 2 строку, умноженную на 3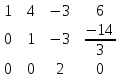 3 строку делим на 2
3 строку делим на 2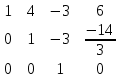 , т.к. ненулевых строк 3, то rang А = 3
, т.к. ненулевых строк 3, то rang А = 3Составим расширенную матрицу и найдем ее ранг:
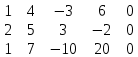 из 2 строки вычитаем 1 строку, умноженную на 2
из 2 строки вычитаем 1 строку, умноженную на 2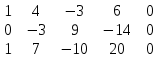 из 3 строки вычитаем 1 строку
из 3 строки вычитаем 1 строку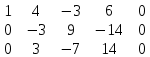 2 строку делим на -3
2 строку делим на -3 из 3 строки вычитаем 2 строку, умноженную на 3
из 3 строки вычитаем 2 строку, умноженную на 3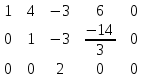 3 строку делим на 2
3 строку делим на 2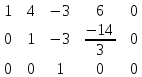 , т.к. ненулевых строк 3, то то rang à = 3
, т.к. ненулевых строк 3, то то rang à = 3Так как rang A = rang Ã, то согласно теореме Кронера-Капелли заданная система алгебраических уравнений совместима. Так как ранги обеих систем меньше 4 (числа неизвестных), данная система имеет бесконечное количество решений.


 Решим заданную систему методом Гаусса:
Решим заданную систему методом Гаусса:х1 + 4х2 – 3х3 + 6х4 = 0
2х1 + 5х2 + х3 – 2х4 = 0 1 строку умножаем на 2 и вычитаем из 2 строки
х1 + 7х2 – 10х3 + 20х4 = 0
х
 1 + 4х2 – 3х3 + 6х4 = 0
1 + 4х2 – 3х3 + 6х4 = 02х1 + 5х2 + х3 – 2х4 – 2х1 – 8х2 + 6х3 – 12х4= 0
х1 + 7х2 – 10х3 + 20х4 = 0
х1 + 4х2 – 3х3 + 6х4 = 0
– 3х2 + 7х3 – 14х4 = 0 из 3 строки вычитаем 1 строку
х1 + 7х2 – 10х3 + 20х4 = 0
х1 + 4х2 – 3х3 + 6х4 = 0
– 3х2 + 7х3 – 14х4 = 0
х1 + 7х2 – 10х3 + 20х4 – х1 – 4х2 + 3х3 – 6х4 = 0
х
 1 + 4х2 – 3х3 + 6х4 = 0
1 + 4х2 – 3х3 + 6х4 = 0– 3х2 + 7х3 – 14х4 = 0 из 2 строки вычитаем 3 строку, умноженную на -1
3х2 – 7х3 + 14х4 = 0
х
 1 + 4х2 – 3х3 + 6х4 = 0
1 + 4х2 – 3х3 + 6х4 = 0– 3х2 + 7х3 – 14х4 + 3х2 – 7х3 + 14х4 = 0
3х2 – 7х3 + 14х4 = 0
х
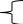 1 + 4х2 – 3х3 + 6х4 = 0
1 + 4х2 – 3х3 + 6х4 = 03х2 – 7х3 + 14х4 = 0
Из уравнения второй подсистемы найдем х2:
3х2 = 7х3 – 14х4
х2 =
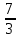 х3 –
х3 –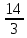 х4
х4Из уравнения первой подсистемы найдем х1:
х1 = - 4*(
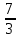 х3–
х3–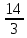 х4) + 3х3 – 6х4
х4) + 3х3 – 6х4 х1 = -
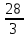 х3 +
х3 +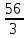 х4 + 3х3 – 6х4
х4 + 3х3 – 6х4 х1 = -
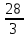 х3 +
х3 +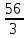 х4 + 3х3 – 6х4
х4 + 3х3 – 6х4 х1 = -