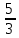Добавлен: 25.10.2023
Просмотров: 45
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

 Для нахождения точки пересечения прямой lи плоскости Р составим и решим систему уравнений:
Для нахождения точки пересечения прямой lи плоскости Р составим и решим систему уравнений:2х + у – 3z – 2 = 0
2x – y + z + 6 = 0 из 2 строки вычитаем 1 строку
x – 2y + 5z – 6 = 0
2х + у – 3z – 2 = 0
2x – y + z + 6 – 2х – у + 3z + 2 = 0
x – 2y + 5z – 6 = 0
2х + у – 3z – 2 = 0
–2y + 4z + 8 = 0 из 3 строки вычитаем 1 строку, деленную на 2
x – 2y + 5z – 6 = 0
2х + у – 3z – 2 = 0
–2y + 4z + 8 = 0
x – 2y + 5z – 6 – х -
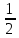 у +
у + 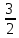 z + 1= 0
z + 1= 02х + у – 3z – 2 = 0
–2y + 4z + 8 = 0 из 3 строки вычитаем 2 строку,деленную на 4 и умноженную на 5
–
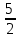 y +
y + 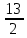 z – 5 = 0
z – 5 = 02х + у – 3z – 2 = 0
–2y + 4z + 8 = 0
–
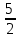 y +
y + 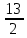 z – 5 +
z – 5 + 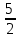 у – 5z – 10 = 0
у – 5z – 10 = 02х + у – 3z – 2 = 0
–2y + 4z + 8 = 0
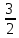 z – 15 = 0
z – 15 = 0Из уравнения 3 строки находим значение:
z = 15 *
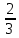 = 10
= 10Из уравнения 2 строки находим значение у:
-2у + 4*10 + 8 = 0
-2у + 48 = 0
у = 24
Из уравнения 1 строки находим значение х:
2х + 24 – 3*10 – 2 = 0
2х – 8 = 0
х = 4
Таким образом, прямая l пересекается с плоскостью Р в точке с координатами (4;24;10).
Ответ:
 =
=  =
= 

x = -2t – 1
y = -8t + 4
z = -4t
 =
=  =
= 
 /
/
(-
 ;
; 
;-
 )
)(4;24;10)
Раздел № 3. Аналитическая геометрия
Задача 1, вариант 3
Составим уравнение прямой АВ, проходящей через точку А (-3;1) и точку В (-2;4):
y = kx + b
П

 одставляем в формулу коорди6наты точек и получаем систему уравнений:
одставляем в формулу коорди6наты точек и получаем систему уравнений:1 = k * (-3) + b
4 = k * (-2) + b
-3k + b = 1
-2k + b = 4
Из 1 уравнения системы находим b = 1 + 3k и подставляем это значение во 2 уравнение:
-2k + 1 + 3k = 4
k + 1 = 4
k = 3, тогда b = 1 + 3*3 = 10
Таким образом, уравнение стороны АВ у = 3x + 10.
Составим уравнение прямой АС, проходящей через точку А (-3;1) и точку С (1;3):
1
 = k * (-3) + b
= k * (-3) + b3 = k * 1 + b
-
 3k + b = 1
3k + b = 1k + b = 3
Из 1 уравнения системы находим b = 1 + 3k и подставляем это значение во 2 уравнение:
k + 1 + 3k = 3
4k = 2
k =
 , тогда b = 1 + 3 *
, тогда b = 1 + 3 *  =
= 
Таким образом, уравнение стороны АС у =
 x +
x +  .
.Составим уравнение прямой BС, проходящей через точку B (-2;4) и точку С (1;3):
4
 = k * (-2) + b
= k * (-2) + b3 = k * 1 + b
-
 2k + b = 4
2k + b = 4k + b = 3
Из 1 уравнения системы находим b = 4 + 2k и подставляем это значение во 2 уравнение:
k + 4 + 2k = 3
3k = -1
k = -
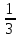 , тогда b = 4 + 2 *(-
, тогда b = 4 + 2 *(- 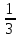 ) =
) = 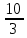
Таким образом, уравнение стороны BС у = -
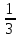 x +
x + 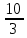 .
.Для нахождения уравнения медианы угла А найдем координаты точки С1 - середины отрезка ВС:
хС1 =
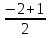
= -
 ; уС1 =
; уС1 = 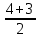 =
= 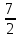 .
.Т
 аким образом, медиана угла А проходит через точку А (-3;1) и точку С1 (-
аким образом, медиана угла А проходит через точку А (-3;1) и точку С1 (-  ;
; 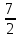 ):
):1 = -3k + b
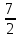 = -
= -  k + b
k + bИз 1 уравнения системы найдем b = 1 + 3k и подставим это значение во 2 уравнение:
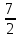 = -
= -  k + 1 + 3k
k + 1 + 3k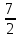 =
=  k + 1
k + 1k =
 /
/ 
k = 1, тогда b = 1 + 3*1 = 4.
Уравнение медианы угла А у = х + 4.
Найдем длину медианы АС1, используя известные координаты точек А и С1:
АС1 =
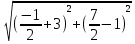 =
= 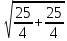 =
= 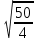 =
= 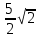
Высота, проведенная из угла А, пересекает сторону ВС, которая умеет уравнение у = -
 x +
x +  .
. Угловой коэффициент k2 прямой, пепендикулярной стороне ВС, равен:
k2 = -1 / k = -1 / -
 = 3, значит уравнение высоты к стороне ВС:
= 3, значит уравнение высоты к стороне ВС:у = 3х + b
Подставляем в уравнение координаты точки А (-3;1) и получаем:
1 = 3*(-3) + b
b = 10
Таким образом, уравнение высоты угла А у = 3х + 10.
Зная уравнение высоты и уравнение стороны ВС треугольника, находим координаты точки их пересечения С2:
у = 3х + 10
у = -

x +
 приравниваем правые части обоих уравнений
приравниваем правые части обоих уравнений3х + 10 = -
 x +
x + 
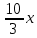 = -
= - 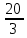
х = -2, тогда у = 3*(-2) + 10 = 4.
Таким образом, высота угла А пересекает прямую ВС в точке С2 (-2;4).
Найдем длину высоты АС1, используя известные координаты точек А и С1:
АС2 =
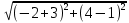 =
= 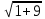 =
= 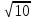 .
.Для нахождения уравнение биссектрисы угла А подставляем уравнения прямых АВ и АС в формулу биссектрис угла:
3х – у + 10 /
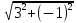 = ± (
= ± ( x – у +
x – у +  ) /
) / 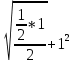
3х – у + 10 /
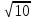 = ± (
= ± ( x – у +
x – у +  ) /
) / 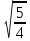
3х – у + 10 /
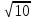 = ± х – 2у + 5 /
= ± х – 2у + 5 / 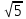
3х – у + 10 = ±
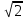 * (х – 2у + 5)
* (х – 2у + 5)3х – у + 10 = ±
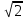 х - 2
х - 2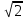 у + 5
у + 5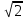
Получаем 2 уравнения:
3х – у + 10 =
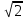 х - 2
х - 2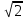 у - 5
у - 5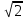 3х – у + 10 =
3х – у + 10 = 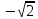
х + 2
 у - 5
у - 5
3х – у + 10 -
 х + 2
х + 2 у - 5
у - 5 = 0 3х – у + 10 +
= 0 3х – у + 10 + х - 2
х - 2 у + 5
у + 5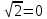
1,59 х + 1,83у + 2,93 = 0 4,41х – 3,83у + 17,07 = 0
Одно из этих уравнений является уравнением биссектрисы внутреннего угла ВАС, а другое – внешнего.
От биссектрисы углы В и С лежат по разные стороны, значит подстановка их координат в уравнение биссектрисы дает нам разные знаки, т.е.
В (-2;4): 1,59*(-2) + 1,83*4 + 2,93 >0
С (1;3): 1,59*1 + 1,83*4 + 2,93
 0, т.е 1 уравнение не соответстует условиям и является уравнением внешнего угла А.
0, т.е 1 уравнение не соответстует условиям и является уравнением внешнего угла А.В (-2;4): 4,41*(-2) – 3,83*4 + 17,07 < 0
С (1;3): 4,41*1-3,83*3 + 17,07 > 0, т.е. 2 уравнение соответствует условиям и является уравнением внутреннего угла А.
Зная уравнение биссектрисы и уравнение стороны ВС треугольника, находим координаты точки их пересечение С3:
у
 = -
= -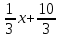
3х – у + 10 =
 х + 2
х + 2 у - 5
у - 5
Подставляем значение у во 2 уравнение системы:
3х +
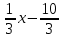 + 10 =
+ 10 =  х + 2
х + 2 * (-
* (-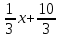 ) - 5
) - 5
 х +
х +  +
+