Добавлен: 25.10.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х3 +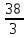 х4
х4
Ответ: х1 = - х3 +
х3 +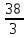 х4
х4
х2 = х3 –
х3 – х4
х4
х3 = х3
х4 = х4
Раздел № 2. Векторная алгебра
Задача 1, вариант 6
Для нахождения общего уравнения плоскости P по координатам точки А (4;5;2) и вектора нормали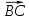 найдем координаты вектора нормали
найдем координаты вектора нормали 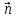 :
:
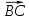 = {Cх – Вх; Су – Ву; Сz – Вz} = {– 1 – 3; 4 – 0; 2 – 1} = {-4;4;1}
= {Cх – Вх; Су – Ву; Сz – Вz} = {– 1 – 3; 4 – 0; 2 – 1} = {-4;4;1}
Для составления общего уравнения плоскости используем формулу:
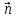 х*(х – ха) +
х*(х – ха) + 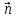 у * (у – уb) +
у * (у – уb) + 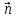 z * (z – zc) = 0
z * (z – zc) = 0
-4 * (x – 4) + 4 * (y – 5) + 1 * (z – 2) = 0
-4х + 16 + 4у – 20 + z – 2 = 0
-4x + 4y + z – 6 = 0
Для составления нормального уравнения плоскости из общего уравнения плоскости, необходимо выполнение одновременно двух условия:
Так как длина нормали в заданном уравнении не равна 1, а D является отрицательным числом, нормальное уравнение не может быть составлено.
Полученное общее уравнение плоскости является полным, следовательно мы можем перевести его в уравнение плоскости в отрезках:
-4x + 4y + z = 6 , разделим обе части уравнения на 6
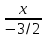
+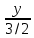 +
+ 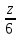 = 1
= 1
Составим общее уравнение P1 по координата точек А (4;5;2) , В (3;0;1) и С (-1;4;2), используя формулу:
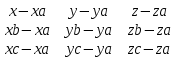 = 0
= 0
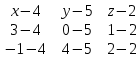 = 0
= 0
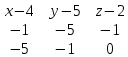 = 0
= 0
(х – 4)*(-5*0 – (-1)*(-1)) – (у – 5)*(-1*0 – (-1)*(-5)) + (z – 2)*(-1*(-1) – (-5)*(-5)) = 0
(x – 4)*(-1) – (y – 5)*(-5) + (z – 2)*(-24) = 0
-x + 4 + 5y – 25 – 24z + 48 = 0
-x + 5y – 24z + 27 = 0
Имея общие уравнении обеих плоскостей, найдем угол между ними по формуле:
cos φ = | -4 * (-1) + 4 * 5 + 1 * (-24) | /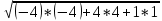 *
* 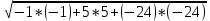 = | 4 + 20 – 24 | /
= | 4 + 20 – 24 | / 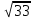 *
* 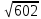 = 0 /
= 0 / 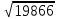 = 0
= 0
Так как косинус угла между плоскостями равен 0, то угол равен 90º и эти плоскости перпендикулярны друг друг.
Найдем расстояние от точки D (5;7;8) до плоскости Р (-4х + 4у + z – 6 = 0) по формуле:
d = | -4*5 + 4*7 + 8*1 - 6| /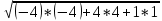 = 10/
= 10/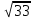
Ответ: -4х + 4у + z – 6 = 0 – общее уравнение Р
 +
+ 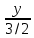 +
+ 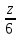 = 1 – уравнение плоскости Р в отрезках
= 1 – уравнение плоскости Р в отрезках
-х + 5у – 24z + 27 = 0 – общее уравнение Р1
90º угол между плоскостями Р и Р1
10/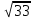 - расстояние между плоскостями.
- расстояние между плоскостями.
Раздел № 2. Векторная алгебра
Задача 2, вариант 8
Найдем точку F, принадлежащую прямой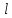 :
:
 Пусть z = 0, тогда получаем следующую систему уравнений:
Пусть z = 0, тогда получаем следующую систему уравнений:
2х + у – 2 = 0
2х – у + 6 = 0
Из первой строки находим у = 2 – 2х и подставляем это значение во вторую строку
2х – (2 – 2х) + 6 = 0
4х + 4 = 0
х = - 1, тогда у = 2 + 2 = 4
Точка F (-1;4;0) принадлежит прямой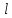 .
.
Найдем координаты направляющего вектора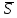 прямойl. Так как он должнен быть перпендикулярен нормалям
прямойl. Так как он должнен быть перпендикулярен нормалям 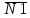 (2;1;-3) и
(2;1;-3) и 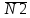 (2;-1;1),
(2;-1;1), 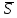 =
= 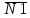 *
* 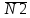
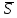 =
= 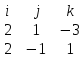 = i *
= i * 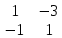 - j *
- j * 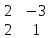 + k *
+ k * 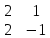 = -2i – 8j - 4k
= -2i – 8j - 4k
Подставляем полученные данные в формулу канонического уравнения и получаем:
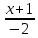 =
= 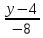 =
= 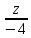
Имея каноническое уравнение прямой и координаты точки F, принадлежащей этой прямой, составим параметрическое уравнение:
x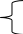 = -2t – 1
= -2t – 1
y = -8t + 4
z = -4t
Направляющим вектором прямой l является вектор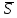 (-2;-8;-4). Так как прямая l1 параллельна прямой l, ее направляющий вектор будет иметь такие же координаты
(-2;-8;-4). Так как прямая l1 параллельна прямой l, ее направляющий вектор будет иметь такие же координаты
, что и направляющий вектор прямой l. По условия прямая l1 проходит через точку М (-1;0;3), значит ее каноническое уравнение будет иметь вид:
 =
= 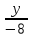 =
= 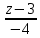
Прямая l проходит через точку F (-1;4;0), прямая l1 проходит через точку М (-1;0;3), направляющий вектор прямой l1 имеет координаты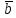 (-2;-8;-4).
(-2;-8;-4).
Определим координаты вектора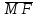 (-1+1;0-4;3-0) = (0;-4;3).
(-1+1;0-4;3-0) = (0;-4;3).
Найдем веркторное произведение векторов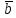 и
и 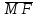 :
:
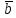 *
* 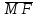 =
= 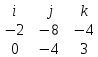 = i *
= i * 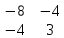 - j *
- j * 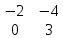 + k *
+ k * 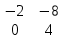 = -40i + 6j + 8k
= -40i + 6j + 8k
Применим формулу расчета расстояния от точки до прямой в пространстве:
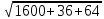 /
/ 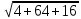 =
= 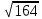 /
/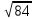 =
= 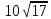 /
/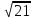
Для нахождения проекции точки М на прямую l запишем уравнение плоскости P1. Для этого определим координаты нормального вектора плоскости P1. Координаты направляющего вектора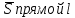 (-2;-8;-4). Он будет являться нормальным вектором плоскости P, перпендикулярной прямой l. Тогда уравнение плоскости P1 будет иметь вид:
(-2;-8;-4). Он будет являться нормальным вектором плоскости P, перпендикулярной прямой l. Тогда уравнение плоскости P1 будет иметь вид:
-2 * (х – (-1)) - 8 * (у – 0) – 4 * (z – 3) = 0
-2х – 2 – 8у – 4z + 12 = 0
-2x – 8y – 4z + 10 = 0


 Чтобы найти точки пересечения прямой l и плоскости P1, решим систему уравнений:
Чтобы найти точки пересечения прямой l и плоскости P1, решим систему уравнений:
2х + у – 3z – 2 = 0
2x – y + z + 6 = 0 из 2 строки вычитаем 1 строку
-2x – 8y - 4z + 10 = 0
2х + у – 3z – 2 = 0
2x – y + z + 6 - 2х – у +3z +2 = 0
-2x – 8y - 4z + 10 = 0
2х + у – 3z – 2 = 0
- 2y + 4z + 8 = 0 из строки вычитаем 1 строку, умноженную на -1
-2x – 8y - 4z + 10 = 0
2х + у – 3z – 2 = 0
- 2y + 4z + 8 = 0
-2x – 8y - 4z + 10 + 2х + у – 3z - 2= 0
2х + у – 3z – 2 = 0
- 2y + 4z + 8 = 0
- 7y – 7z + 8 = 0
Из 3 уравнения системы найдем z:
z =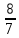 - у
- у
Из 2 уравнения системы найдем y:
-2у + 4 * (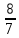 – у) + 8 = 0
– у) + 8 = 0
-2у +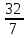 - 4у + 8 = 0
- 4у + 8 = 0
-6у +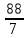 = 0
= 0
6у =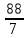
у =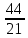
z =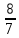 -
- 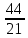
z = -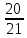
2x +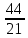 - 3 * (-
- 3 * (-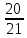 ) – 2 = 0
) – 2 = 0
2x +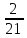 +
+ 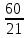 = 0
= 0
2x +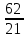 = 0
= 0
x = -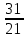
Таким образом, координаты проекции точки М на прямую l (-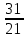 ;
; 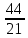 ;-
;-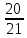 ).
).





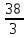 х4
х4 Ответ: х1 = -
 х3 +
х3 +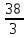 х4
х4 х2 =
 х3 –
х3 – х4
х4х3 = х3
х4 = х4
Раздел № 2. Векторная алгебра
Задача 1, вариант 6
Для нахождения общего уравнения плоскости P по координатам точки А (4;5;2) и вектора нормали
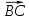 найдем координаты вектора нормали
найдем координаты вектора нормали 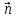 :
: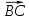 = {Cх – Вх; Су – Ву; Сz – Вz} = {– 1 – 3; 4 – 0; 2 – 1} = {-4;4;1}
= {Cх – Вх; Су – Ву; Сz – Вz} = {– 1 – 3; 4 – 0; 2 – 1} = {-4;4;1}Для составления общего уравнения плоскости используем формулу:
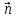 х*(х – ха) +
х*(х – ха) + 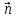 у * (у – уb) +
у * (у – уb) + 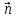 z * (z – zc) = 0
z * (z – zc) = 0-4 * (x – 4) + 4 * (y – 5) + 1 * (z – 2) = 0
-4х + 16 + 4у – 20 + z – 2 = 0
-4x + 4y + z – 6 = 0
Для составления нормального уравнения плоскости из общего уравнения плоскости, необходимо выполнение одновременно двух условия:
-
Длина нормали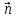 должна находиться по формуле оpen
должна находиться по формуле оpen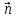 |=
|= 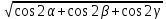 и быть равной 1, где α – абсцисса нормали, β – ордината нормали, γ – аппликата нормали;
и быть равной 1, где α – абсцисса нормали, β – ордината нормали, γ – аппликата нормали; -
D (в нашем уравнении - 6) должно быть положительным числом.
Так как длина нормали в заданном уравнении не равна 1, а D является отрицательным числом, нормальное уравнение не может быть составлено.
Полученное общее уравнение плоскости является полным, следовательно мы можем перевести его в уравнение плоскости в отрезках:
-4x + 4y + z = 6 , разделим обе части уравнения на 6
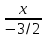
+
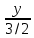 +
+ 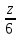 = 1
= 1Составим общее уравнение P1 по координата точек А (4;5;2) , В (3;0;1) и С (-1;4;2), используя формулу:
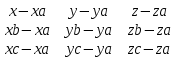 = 0
= 0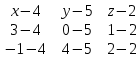 = 0
= 0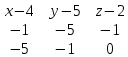 = 0
= 0(х – 4)*(-5*0 – (-1)*(-1)) – (у – 5)*(-1*0 – (-1)*(-5)) + (z – 2)*(-1*(-1) – (-5)*(-5)) = 0
(x – 4)*(-1) – (y – 5)*(-5) + (z – 2)*(-24) = 0
-x + 4 + 5y – 25 – 24z + 48 = 0
-x + 5y – 24z + 27 = 0
Имея общие уравнении обеих плоскостей, найдем угол между ними по формуле:
cos φ = | -4 * (-1) + 4 * 5 + 1 * (-24) | /
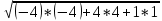 *
* 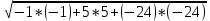 = | 4 + 20 – 24 | /
= | 4 + 20 – 24 | / 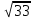 *
* 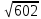 = 0 /
= 0 / 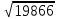 = 0
= 0Так как косинус угла между плоскостями равен 0, то угол равен 90º и эти плоскости перпендикулярны друг друг.
Найдем расстояние от точки D (5;7;8) до плоскости Р (-4х + 4у + z – 6 = 0) по формуле:
d = | -4*5 + 4*7 + 8*1 - 6| /
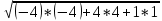 = 10/
= 10/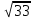
Ответ: -4х + 4у + z – 6 = 0 – общее уравнение Р
 +
+ 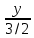 +
+ 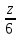 = 1 – уравнение плоскости Р в отрезках
= 1 – уравнение плоскости Р в отрезках-х + 5у – 24z + 27 = 0 – общее уравнение Р1
90º угол между плоскостями Р и Р1
10/
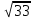 - расстояние между плоскостями.
- расстояние между плоскостями.Раздел № 2. Векторная алгебра
Задача 2, вариант 8
Найдем точку F, принадлежащую прямой
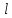 :
: Пусть z = 0, тогда получаем следующую систему уравнений:
Пусть z = 0, тогда получаем следующую систему уравнений:2х + у – 2 = 0
2х – у + 6 = 0
Из первой строки находим у = 2 – 2х и подставляем это значение во вторую строку
2х – (2 – 2х) + 6 = 0
4х + 4 = 0
х = - 1, тогда у = 2 + 2 = 4
Точка F (-1;4;0) принадлежит прямой
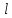 .
.Найдем координаты направляющего вектора
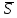 прямойl. Так как он должнен быть перпендикулярен нормалям
прямойl. Так как он должнен быть перпендикулярен нормалям 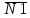 (2;1;-3) и
(2;1;-3) и 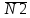 (2;-1;1),
(2;-1;1), 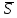 =
= 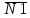 *
* 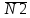
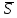 =
= 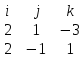 = i *
= i * 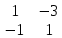 - j *
- j * 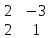 + k *
+ k * 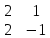 = -2i – 8j - 4k
= -2i – 8j - 4kПодставляем полученные данные в формулу канонического уравнения и получаем:
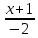 =
= 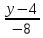 =
= 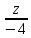
Имея каноническое уравнение прямой и координаты точки F, принадлежащей этой прямой, составим параметрическое уравнение:
x
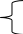 = -2t – 1
= -2t – 1y = -8t + 4
z = -4t
Направляющим вектором прямой l является вектор
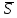 (-2;-8;-4). Так как прямая l1 параллельна прямой l, ее направляющий вектор будет иметь такие же координаты
(-2;-8;-4). Так как прямая l1 параллельна прямой l, ее направляющий вектор будет иметь такие же координаты
, что и направляющий вектор прямой l. По условия прямая l1 проходит через точку М (-1;0;3), значит ее каноническое уравнение будет иметь вид:
 =
= 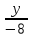 =
= 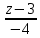
Прямая l проходит через точку F (-1;4;0), прямая l1 проходит через точку М (-1;0;3), направляющий вектор прямой l1 имеет координаты
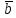 (-2;-8;-4).
(-2;-8;-4).Определим координаты вектора
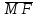 (-1+1;0-4;3-0) = (0;-4;3).
(-1+1;0-4;3-0) = (0;-4;3).Найдем веркторное произведение векторов
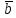 и
и 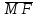 :
: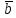 *
* 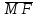 =
= 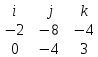 = i *
= i * 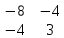 - j *
- j * 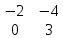 + k *
+ k * 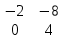 = -40i + 6j + 8k
= -40i + 6j + 8kПрименим формулу расчета расстояния от точки до прямой в пространстве:
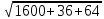 /
/ 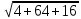 =
= 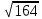 /
/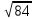 =
= 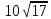 /
/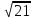
Для нахождения проекции точки М на прямую l запишем уравнение плоскости P1. Для этого определим координаты нормального вектора плоскости P1. Координаты направляющего вектора
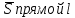 (-2;-8;-4). Он будет являться нормальным вектором плоскости P, перпендикулярной прямой l. Тогда уравнение плоскости P1 будет иметь вид:
(-2;-8;-4). Он будет являться нормальным вектором плоскости P, перпендикулярной прямой l. Тогда уравнение плоскости P1 будет иметь вид:-2 * (х – (-1)) - 8 * (у – 0) – 4 * (z – 3) = 0
-2х – 2 – 8у – 4z + 12 = 0
-2x – 8y – 4z + 10 = 0


 Чтобы найти точки пересечения прямой l и плоскости P1, решим систему уравнений:
Чтобы найти точки пересечения прямой l и плоскости P1, решим систему уравнений:2х + у – 3z – 2 = 0
2x – y + z + 6 = 0 из 2 строки вычитаем 1 строку
-2x – 8y - 4z + 10 = 0
2х + у – 3z – 2 = 0
2x – y + z + 6 - 2х – у +3z +2 = 0
-2x – 8y - 4z + 10 = 0
2х + у – 3z – 2 = 0
- 2y + 4z + 8 = 0 из строки вычитаем 1 строку, умноженную на -1
-2x – 8y - 4z + 10 = 0
2х + у – 3z – 2 = 0
- 2y + 4z + 8 = 0
-2x – 8y - 4z + 10 + 2х + у – 3z - 2= 0
2х + у – 3z – 2 = 0
- 2y + 4z + 8 = 0
- 7y – 7z + 8 = 0
Из 3 уравнения системы найдем z:
z =
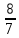 - у
- уИз 2 уравнения системы найдем y:
-2у + 4 * (
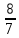 – у) + 8 = 0
– у) + 8 = 0-2у +
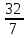 - 4у + 8 = 0
- 4у + 8 = 0-6у +
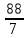 = 0
= 06у =
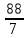
у =
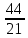
z =
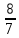 -
- 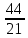
z = -
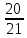
2x +
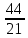 - 3 * (-
- 3 * (-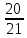 ) – 2 = 0
) – 2 = 02x +
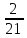 +
+ 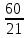 = 0
= 02x +
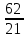 = 0
= 0x = -
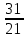
Таким образом, координаты проекции точки М на прямую l (-
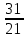 ;
; 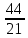 ;-
;-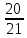 ).
).



